Теория вероятностей математическая статистика
Решение• . Решаем задачу по формуле Бейеса.
1 шаг. Формируем гипотезы: В1 – выбор первой урны; В2 – выбор второй урны; В3 – выбор третьей урны. Определяем их вероятности.
Априори (до опыта) все гипотезы равновероятны:
Р(В1) = Р(В2) = Р(В3) = 1/3.
2 шаг. Анализ ситуации: Произошло событие А – появление белого шара.
3 шаг. Найдем условные вероятности: ; ; .
4 шаг. По формуле Бейеса находим вероятность того, что шар был вынут из первой урны:
. Аналогично ;
.
71
Теория вероятностей математическая статистика
Задача 4. Прибор может собираться из высококачественных деталей и из деталей обычного качества. 40% приборов собирается из высококачественных деталей. Если прибор собран из высококачественных деталей, его надежность (вероятность безотказной работы) за время t равна 0,95; если из деталей обычного качества – его надежность равна 0,7. Прибор испытывался в течение времени t и работал безотказно. Найти вероятность того, что он собран из высококачественных деталей.
72
Теория вероятностей математическая статистика
Решение• .
1 шаг. Формируем гипотезы: В1- прибор собран из высококачественных деталей; В2 - прибор собран из деталей обычного качества.
Вероятности этих гипотез до опыта известны: Р(В1) = 0,4; Р(В2) = 0,6.
2 шаг. Анализ ситуации: В результате опыта наблюдено событие
А – прибор безотказно работал время t.
3 шаг. Учет условных вероятностей этого события при гипотезах В1 и В2 :
РВ1(А) = 0,95; РВ2(А) = 0,7.
4 шаг. По формуле Бейеса находим искомую вероятность (вероятность того, что прибор изготовлен из высококачественных деталей):
73
Теория вероятностей математическая статистика
Задача 5. Прибор состоит из двух узлов: работа каждого узла безусловно необходима для работы прибора в целом. Надежность (безотказность работы в течение времени t ) первого узла равна р1, второго р2. Прибор испытывался в течение времени t, в
результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.
74
Теория вероятностей математическая статистика
Решение• .
1 шаг. Формируем гипотезы: В0 – оба узла исправны; В1 – первый узел отказал, а второй исправен; В2 – первый узел исправен, а второй отказал; В3 – оба узла отказали.
Определяем их вероятности.
Вероятности гипотез: Р(В0) = p1p2; Р(В1) = (1 – p1)p2; Р(В2) = p1 (1 – p2); Р(В3) = (1 – p1)(1 - p2).
2.шаг. Анализ дополнительной информации: Наблюдалось
событие А – прибор отказал.
3.шаг. Определяем условные вероятности. Р(В0) = 0; Р(В1) = Р(В2) = Р(В3) = 1.
4 шаг. По формуле Бейеса находим искомую вероятность (переоцениваем вероятность гипотезы В1):
PA(B1) = .
75
Теория вероятностей математическая статистика
ЗАДАЧИ НА ФОРМУЛУ БЕРНУЛЛИ
76
Теория вероятностей и математическая статистика
•Бернулли показал, что вероятность появления
события А k раз в n независимых испытаниях определяется выражением
или
где q=1-p, а k = 0, … ,n.
Эту формулу называют формулой Бернулли.
77
Теория вероятностей математическая статистика
Задача 6. Монета бросается пять раз. Какова вероятность того, что число выпавших гербов будет больше числа выпавших цифр?
78
Теория вероятностей математическая статистика
Решение• . Обозначим A искомое событие — число выпавших гербов больше числа цифр при пяти бросаниях монеты. Для выполнения события A необходимо, чтобы число гербов при пяти бросаниях монеты было 3, 4 или 5 (при этом цифр будет соответственно 2, 1 или 0).
По формуле Бернулли получим
P(A) = P5(3) + P5(4) + P5(5) = =
= 10 0,53 0,52 + 5 0,54 0,5 + 0,55 = 0,50.
79
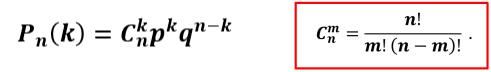
Теория вероятностей математическая статистика
Задача 7. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести? Ничьи во внимание не принимаются.
80