Теория вероятностей и математическая статистика

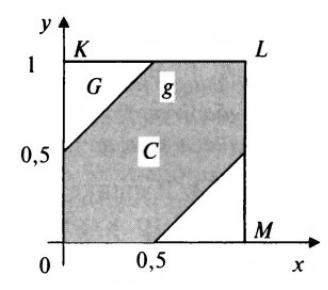
По условию 0 x 1, 0 y 1. Этим неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату ОKLM со стороной, равной 1 (см. рис. 1). Событие С – встреча двух лиц произойдет, если разность между х и y не превышает 0,5 часа (по абсолютной величине), т.е. y - x 0,5.

Решение последнего неравенства есть полоса

х – 0,5 y x + 0,5, которая на рисунке 1 представляет заштрихованную область g.

Рис.1

41

Теория вероятностей и математическая статистика

•

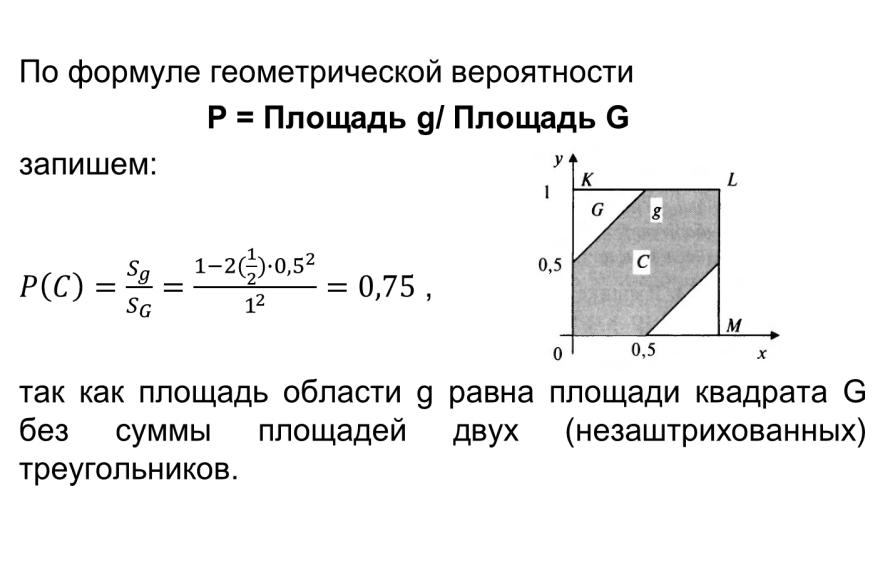
По формуле геометрической вероятности

Р = Площадь g/ Площадь G

запишем:

,

так как площадь области g равна G без суммы площадей двух (незаштрихованных) треугольников.

42

Теория вероятностей и математическая статистика

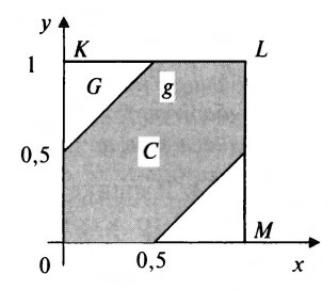
В этой задаче возможно бесконечное несчетное множество элементарных исходов (событий) – точек (x,y) квадрата OKLM, координаты x и y которых равны моментам прихода к месту встречи двух лиц (см. рис. 1). То есть пространство элементарных событий - квадрат OKLM. Событие А, состоящее в том, что встреча двух лиц произойдет, есть заштрихованная область g на рисунке – часть квадрата, то есть подмножество пространства : А .

43

Теория вероятностей и математическая статистика

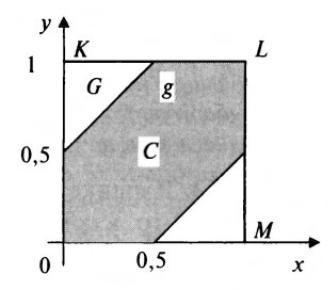
Само пространство элементарных событий представляет собой событие, происходящее всегда (при любом элементарном исходе ), и называется достоверным событием. Таким образом, выступает в двух качествах: множества всех элементарных исходов и достоверного события.

44

Теория вероятностей и математическая статистика

•Несколько событий А1, А2, …, Аn образуют полную группу

(полную систему), если их сумма представляет все пространство элементарных событий, а сами события несовместные, т.е.

и AiAj = (i j).

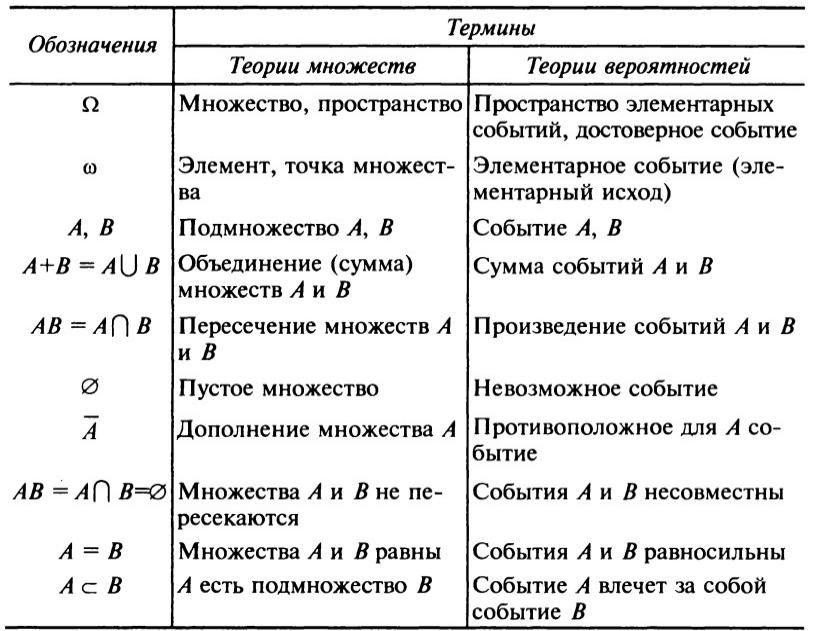
Таким образом, под операциями над событиями понимают операции над соответствующими множествами.

Соответствие терминов теории множеств и теории вероятностей показано на следующем слайде.

46

Теория вероятностей и математическая статистика

47

Теория вероятностей и математическая статистика

На основании изложенной трактовки событий как множеств вернемся к аксиоматическому построению теории вероятностей, о котором мы с вами говорили на первой лекции.

48

Теория вероятностей и математическая статистика

Аксиоматика теории вероятностей исходит из основных свойств вероятности событий, к которым применимо классическое или статистическое определение вероятности.

Аксиоматическое определение вероятности как частные случаи включает в себя и классическое, и статистическое определения и преодолевает недостатки каждого из них.

49

Теория вероятностей и математическая статистика

Впервые идея аксиоматического построения теории вероятностей была высказана российским академиком С.Н. Бернштейном, исходившим из качественного сравнения событий по их большей или меньшей вероятности. Как мы уже знаем, в начале 30-х годов

академик А.Н. Колмогоров разработал иной подход, связывающий теорию вероятностей с современной теорией функций и теорией множеств. Этот подход в настоящее время является общепринятым.

50