
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)
ШИФРАТОРЫ И ДЕШИФРАТОРЫ
Отчет по лабораторной работе №2 по дисциплине «Электроника и схемотехника 2»
Вариант №19
Студент гр.
Руководитель пр
Томск 2022
Введение
Цель работы – научиться создавать шифраторы и дешифраторы на разных базисах и решать задачу увеличения их размерности.
Постановка задачи:
1.Составьте таблицу истинности для схем, заданных согласно варианту. Написать формулы для всех выходов в СДНФ или СКНФ и привести формулы к требуемому базису согласно варианту.
2.Собрать схему на холстах .bdf согласно полученным формулам и создать символ для полученного блока.
3.Создать схему устройства согласно варианту большей размерности на основе созданного ранее символа.
4.Промоделировать работу всех схем в двух режимах.
5. Повторить пп. 2-4, только для описания устройств вместо схем на холстах .bdf использовать заданный вариантом HDL.
Задание по варианту:
Шифратор CD: 8-3; И, ИЛИ, НЕ; 16-4. Дешифратор DC: 2-4; ИЛИ-НЕ; 3-8. HPRI: 10-4; И-НЕ; -.
HDL - SystemVerilog
2

1.ШИФРАТОР 8-3
1.1ТАБЛИЦА ИСТИННОСТИ
Шифраторы предназначены для преобразования кода «1 из N» в двоичный. При подаче на один (обязательно на один, и не более) из входов шифратора на его выходе формируется двоичный код номера возбужденной входной линии. Полный двоичный шифратор имеет 2 входов и выходов.
Для информировании о том, что на вход была подана только одна единица, сигнализирует выход .
Также на вход подается сигнал EI, который разрешает работу данного шифратора.
Таблица 1.1 отражает таблицу истинности для шифратора 8-3. Таблица 1.1 – Таблица истинности шифратора 8-3.
|
|
|
|
Входы |
|
|
|
|
|
Выходы |
|
||
E |
|
|
|
x |
|
|
|
|
|
a |
|
G |
|
|
7 |
6 |
5 |
4 |
|
3 |
2 |
1 |
0 |
2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
x |
x |
x |
x |
|
x |
x |
x |
x |
0 |
0 |
0 |
0 |
1.2 ФОРМУЛА
По таблице истинности 1.1 составим формулы для трех выходов и
сигнала G в виде СДНФ: |
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
= (( |
7 |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅) |
|||||||
|
|
|
6 |
|
5 |
|
4 |
3 |
2 |
1 |
0 |
||
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
||
|
|
|
|
5 |
|
7 |
|
6 |
4 |
3 |
2 |
1 |
0 |
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
||
|
|
|
|
3 |
|
7 |
|
6 |
5 |
4 |
2 |
1 |
0 |
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅) |
|
|
|
|
|
1 |
|
7 |
|
6 |
5 |
4 |
3 |
2 |
0 |
|
|
= (( |
|
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅) |
|||||||
1 |
7 |
|
6 |
|
5 |
|
4 |
3 |
2 |
1 |
0 |
||
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
||
|
|
|
|
6 |
|
7 |
|
5 |
4 |
3 |
2 |
1 |
0 |
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
||
|
|
|
|
3 |
|
7 |
|
6 |
5 |
4 |
2 |
1 |
0 |
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
||
|
|
|
|
2 |
|
7 |
|
6 |
5 |
4 |
3 |
1 |
0 |
3
|
2 |
= (( |
7 |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅) |
|
||||||||
|
|
|
6 |
|
5 |
|
4 |
3 |
2 |
1 |
0 |
|
|||
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
6 |
|
7 |
|
5 |
4 |
3 |
2 |
1 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
5 |
|
7 |
|
6 |
4 |
3 |
2 |
1 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
4 |
|
7 |
|
6 |
5 |
3 |
2 |
1 |
0 |
|
= (( |
|
̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅) |
|
||||||||||||
|
|
7 |
|
|
6 |
|
5 |
|
4 |
3 |
2 |
1 |
0 |
|
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
6 |
|
7 |
|
5 |
4 |
3 |
2 |
1 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
5 |
|
7 |
|
6 |
4 |
3 |
2 |
1 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
4 |
|
7 |
|
6 |
5 |
3 |
2 |
1 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
3 |
|
7 |
|
6 |
5 |
4 |
2 |
1 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ ̅̅̅) |
|||
|
|
|
|
|
2 |
|
7 |
|
6 |
5 |
4 |
3 |
1 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
) |
|
|
|
|
|
|
1 |
|
7 |
|
6 |
5 |
4 |
3 |
2 |
0 |
|
|
|
|
|
( |
|
̅̅̅ |
|
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
̅̅̅ |
) |
|
|
|
|
|
|
0 |
|
7 |
|
6 |
5 |
4 |
3 |
2 |
1 |
|
В формулах присутствует только базисные элементы, заданные варианту: И, ИЛИ, НЕ.
1.3 ФУНКЦИОНАЛЬНАЯ СХЕМА
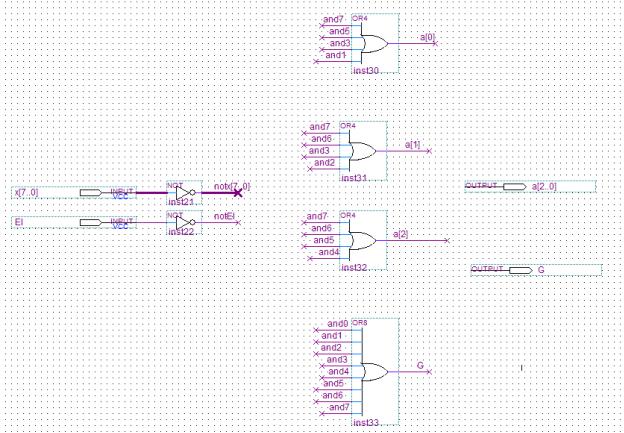
На рисунках 1.1-1.2 представлена функциональная схема шифратора 8-3.
Рисунок 1.1 – Функциональная схема шифратора 8-3
4

Рисунок 1.2 – Функциональная схема шифратора 8-3 На рисунке 1.1 указаны входы и выходы, описанные в пункте 1.1.
Логические элементы И, ИЛИ, НЕ присутствуют на обоих рисунках 1.1 и 1.2.
1.4 РЕЗУЛЬТАТ МОДЕЛИРОВАНИЯ СХЕМЫ
На рисунке 1.3 представлено моделирование шифратора 8-3 в режиме
Timing.
Рисунок 1.3 – Моделирование в режиме Timing
На рисунке 1.4 представлено моделирование шифратора 8-3 в режиме
Functional.
Рисунок 1.4 – Моделирование в режиме Functional
Помимо основных состояниях, при которых шифратор работает правильно, были проверены состояния, при которых сигнал должен сигнализировать о том, что на вход подан не унитарный код.
По результатам моделирования результат работы собранной схемы соответствует таблице истинности.
5
1.5 ОПИСАНИЕ С ПОМОЩЬЮ HDL
По варианту используется SystemVerilog.
Ниже приведен код описывающий устройство шифратора 8-3: module CD8_3 (
input logic [7:0] x, input logic EI, output logic [2:0]a, output logic G
);
always_comb begin G = 1'b1;
if (EI) case(x)
8'b10000000: a = 3'b111; 8'b01000000: a = 3'b110; 8'b00100000: a = 3'b101; 8'b00010000: a = 3'b100; 8'b00001000: a = 3'b011; 8'b00000100: a = 3'b010; 8'b00000010: a = 3'b001; 8'b00000001: a = 3'b000; default: begin
a = 3'b000; G = 0;
end endcase
else begin
a = 3'b000; G = 0;
end end
endmodule
На рисунке 1.5 представлена схема из RTL Viewer для кода выше.
6
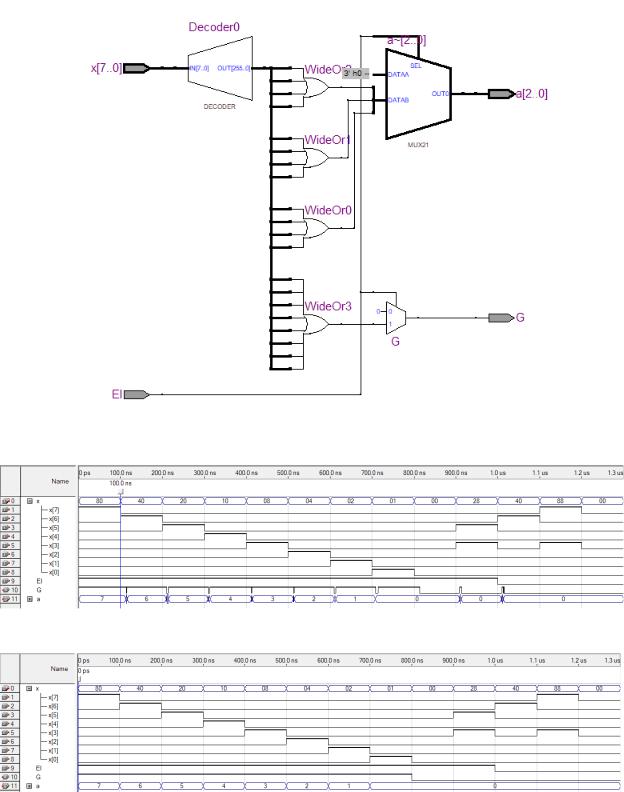
Рисунок 1.5 – RTL Viewer представление
На рисунке 1.6 представлено моделирование в режиме Timing.
Рисунок 1.6 – Моделирование в режиме Timing
На рисунке 1.7 представлено моделирование в режиме Functional.
Рисунок 1.7 – Моделирование в режиме Functional
1.6 МАСШТАБИРОВАНИЕ ШИФРАТОРА
По варианту необходимо реализовать работу шифратора 16-4 на основе 8-
3.
Таблица истинности для шифратора 16-4 представлена в таблице 1.2.
7

Таблица 1.2 - Таблица истинности для шифратора 16-4
|
|
|
|
|
|
Входы |
|
|
|
|
|
|
|
|
|
|
Выходы |
|
|||||
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
G |
|
|
15 |
14 |
13 |
13 |
12 |
11 |
10 |
|
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
3 |
2 |
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
0 |
0 |
0 |
0 |
0 |
||
В соответствии таблицей истинности на основе шифратора 8-3 была разработана схема шифратора 16-4. Функциональная схема масштабированного шифратора 16-4 приведена на рисунке 1.8
8
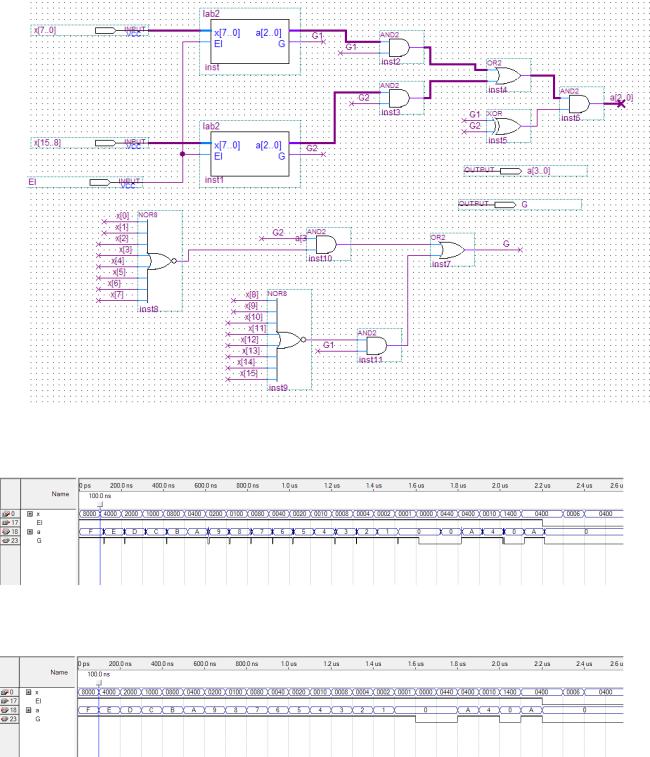
Рисунок 1.8 – Функциональная схема шифратора 16-4 На рисунке 1.9 представлено моделирование шифратора 16-4 в режиме
Timing.
Рисунок 1.9 – Моделирование в режиме Timing
На рисунке 1.10 представлено моделирование шифратора 16-4 в режиме
Functional.
Рисунок 1.10 – Моделирование в режиме Functional
По результатам моделирования видно, что работа схемы соответствует таблице истинности 1.2.
С помощью SystemVerilog также была описана схема шифратора 16-4 с использованием масштабирования. За основу взят шифратор 8-3, описанный в пункте 1.5.
module CD16_4( input logic [15:0] x, input logic EI,
9
output logic [3:0] a, output logic G
);
logic G1, G2; logic [2:0] cd70; logic [2:0] cd158;
CD8_3 CD1(x[7:0], EI, cd70, G1); CD8_3 CD2(x[15:8], EI, cd158, G2);
assign a[0] = (cd70[0] & G1 | cd158[0] & G2) & (G1 ^ G2); assign a[1] = (cd70[1] & G1 | cd158[1] & G2) & (G1 ^ G2); assign a[2] = (cd70[2] & G1 | cd158[2] & G2) & (G1 ^ G2);
assign a[3] = ~(x[7] | x[6] | x[5] | x[4] | x[3] | x[2] | x[1] | x[0]) & G2;
assign G = a[3] | (G1 & ~(x[15] | x[14] | x[13] | x[12] | x[11] | x[10] | x[9] | x[8]));
endmodule
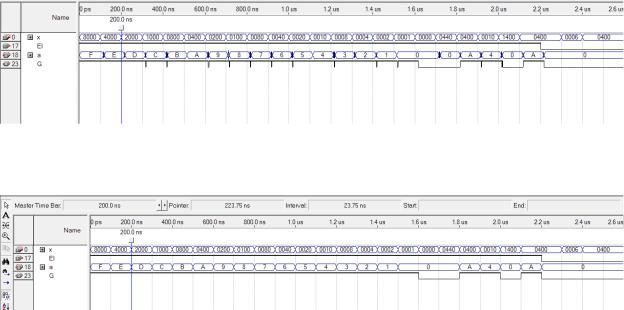
Результат моделирования шифратора 16-4 описанный с помощью SystemVerilog в режиме Timing представлен на рисунке 1.11.
Рисунок 1.11 – Моделирование в режиме Timing
На рисунке 1.12 представлен результат моделирования в режиме
Functional.
Рисунок 1.12 – Моделирование в режиме Functional
По результатам моделирования видно, что работа схемы соответствует таблице истинности 1.2.
На рисунке 1.13 представлена схема из RTL Viewer для кода, описывающего шифратор 16-4
10
