2. Болт подвержен действию переменных нагрузок

Болты, винты, шпильки, находящиеся под действием переменных нагрузок, рассчитываются на выносливость и становятся на рабочее место с предварительной затяжкой Р_З. В большинстве случаев переменная внешняя нагрузка на болт изменяется по отнулевому (пульсирующему) циклу. Так, например, нагружены шатунные болты.

Переменная внешняя нагрузка изменяется от 0 до Р и распределяется между стыком и болтом таким образом, что на болт приходится часть её, равная “χР”. Значит на болт действует сила Р₀ = Р_З + χР.

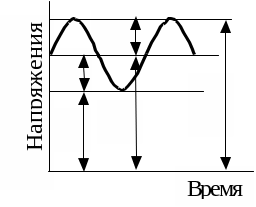
Рис. 6.73. Схема нагружения напряженного резьбового соединения при переменных напряжениях

Напряжение начальной затяжки болта равно:

[σ]_З = (0,4…0,6)σ_Т;

где σ_Т – предел текучести материала болта при растяжении.

Амплитуда напряжений цикла:

Среднее напряжение цикла:

.

Максимальное напряжение цикла:

или .

Расчёт на выносливость болтов в этом случае производится как проверочный по коэффициенту запаса прочности по амплитуде, а иногда по коэффициенту запаса прочности по максимальному напряжению.

Для проведения этого расчёта болт предварительно рассчитывается из условия статической прочности его при отсутствии последующей затяжки по формуле:

или с последующей затяжкой:

Затем последовательно определяются Р_З; Хχ; Р; σ_З. После чего болт рассчитывается на выносливость.

Так, расчёт болта на выносливость по запасу прочности по амплитуде производится по формуле:

.

Расчёт болта на выносливость по запасу прочности по максимальному напряжению осуществляется по уравнению:

где: n_a – коэффициент запаса прочности по амплитуде;

[n_a] – допускаемый коэффициент запаса прочности по амплитуде. [n_a] = 2,5…4;

n – действительный коэффициент запаса прочности по максимальному напряжению;

[n] – допускаемый коэффициент запаса прочности по максимальному напряжению.

ε – масштабный коэффициент, учитывающий влияние размеров детали на предел выносливости. Величина “ ” находится из графиков или таблицы;

σ_RP – предел выносливости материала болта при растяжении, при симметричном цикле изменения напряжений;

K_{Б –} эффективный коэффициент концентрации напряжений. Для нарезанных болтов из углеродистой стали: K_Б = 4 (при d₁ = 16) и K_Б = 6 (при d₁ ≥ 24 мм);

σ_Т – предел текучести материала болта.

8. Примеры расчёта резьбовых соединений

Пример 1. Рассчитать болты дисковой муфты (рис. 6.15.). Передаваемая мощность N = 40 кВт; угловая скорость ω = 30 с^-1; диаметр окружности центров болтов D = 240 мм. Материал полумуфт и болтов – сталь Ст. 3, число болтов z = 4 . Затяжка болтов неконтролируемая. Действующие нагрузки считать статическими. Расчет болтов выполнить для двух случаев установки в отверстия: с зазором и без зазора.

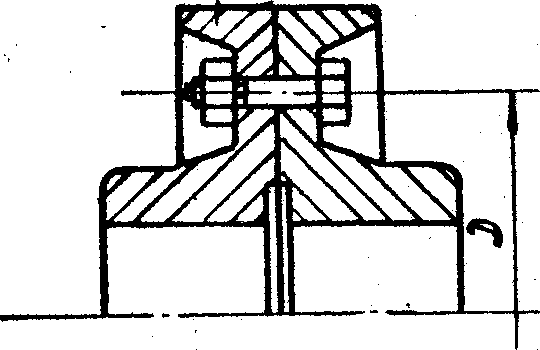
Рис. 6.74. Схема к расчету болтов дисковой муфты

Решение.

Вращающий момент, передаваемый муфтой

.

Окружная сила, воспринимаемая одним болтом

.

а) – расчет болтов, установленных в отверстия с зазором

По табл.4 [1] для стали Ст. 3 выбираем [σ]_Т = 220 МПа. По табл.12 [3] выбираем коэффициент запаса прочности при неконтролируемой затяжке n = 2,5.

Определяем допускаемые напряжения на растяжение, срез и смятие [1,§37]

.

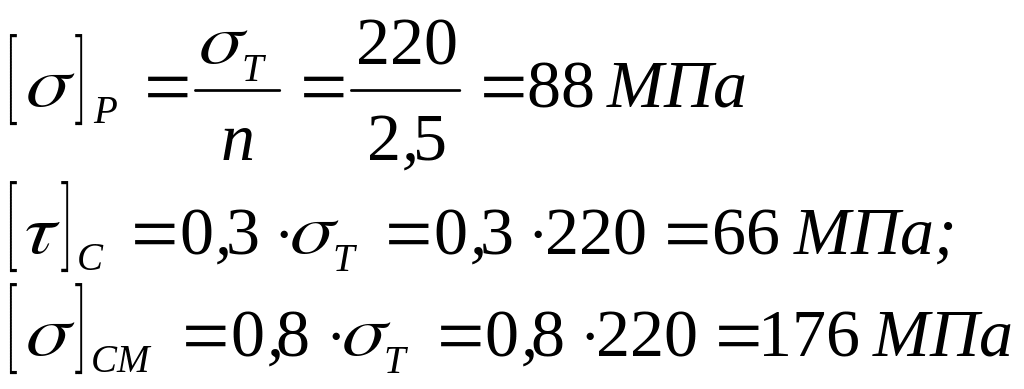Принимаем коэффициент трения между полумуфтами f = 0,15 и коэффициент запаса от сдвига полумуфт К = 1,2 [3,§25.]. Потребная сила затяжки болта.

Эквивалентное напряжение с учетом скручивания болта при затяжке

,

откуда внутренний диаметр резьбы

.

По табл. 3.3 [5] выбираем болт с ближайшим большим внутренним диаметром резьбы, т.е. болт с резьбой М 24, d₁ = 20,752 мм, Р = 3 мм.

Болт также можно выбрать по табл.3.10 [5] в зависимости от величины Р_ЗАТ и принятого материала.

б) расчет болтов, установленных в отверстия без зазора.

Из условия прочности на срез определяем потребный диаметр стержня болта

Выбираем ближайший больший по размеру болт – М 8.

Очевидно существенное уменьшение размеров болта (и всего соединения), установленного в отверстие без зазора (сравнить М 8 и М 24).

Пример 2. Рассчитать болт клеммового соединения (рис. 6.16), если D = 20 мм; Р = 400 кН; а = 20 мм; ℓ = 300 мм. Материал вала – сталь; материал рычага – чугун. Затяжка болта неконтролируемая.

Решение.

При расчете клеммового соединения с прорезью дополнительной силой затяжки болтов пренебрегают или учитывают её введением коэффициента К = 1,1. [1].

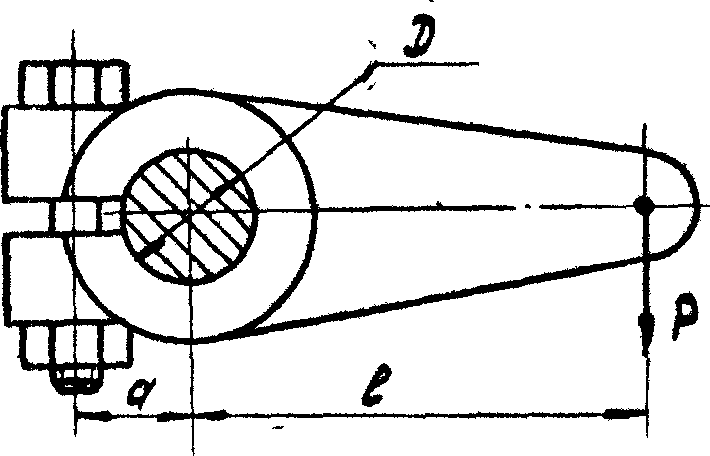
Рис. 6.75. Схема к расчету клеммового соединения

Примем, что момент сил трения на 20% превышает внешний момент М, т.е. коэффициент запаса от сдвига К = 1,2, тогда

М_Т = 1,2М = 1,2P·ℓ.

Принимаем коэффициент трения f = 0,15.

Усилие затяжки болта определяем по формуле [3]

По условию компоновки (рис. 9) диаметр болта не должен быть более 18 мм.

Определяем потребный диаметр болта из расчета (пример 8) или непосредственно по табл. 3.10 [5] выбираем болт М16 материал 12XH2. Предельная продольная осевая нагрузка для выбранного болта Р = 18 кН.

Пример 3. Рассчитать болты, с помощью которых полоса 1 прикреплена к металлической колонне 2 (рис. 6.17). Угол α = 30°; Р = 20 кН. Коэффициент трения в плоскости стыка f = 0,2. Материал полосы и колонны – сталь Ст.3. σ_Т = 240 МПа. Материал болтов – сталь 45 закаленная. σ_Тδ = 580 МПа. Затяжка болтов неконтролируемая.

Рис. 6.76

Решение.

Разложим силу Р на горизонтальную (Р_x) и вертикальную (Р_y) составляющие:

Р_y = P·cos·30^o = 20·0,86 = 17,2 кН

Р_x = P·sin·30^o = 20·0,5 = 10 кН

Перенесем силы Р_x и Р_y в центр тяжести треугольника c вершинами, совпадающими с центрами отверстий под болты (рис.20) и добавим моменты

М_Рx = – Р_x · b = – 10 · 0,3 = – 3 кН·м;

М_Рy = Р_y·(а+С) = 17,2·0,54 = 9,29 кН·м,

где С = (1/3)·ℓ = 40 мм.

Результирующий момент

М_R = М_Р  – М_Рx = 6,29 кН·м

Силы и момент действуют в плоскости стыка и должны быть уравновешены силами трения.

Силу Р_y уравновешивают три силы:

Р′_y = Р_y /Z = 17,2/3 = 5,73 кН·м;

Cилу Р_x тоже уравновешивают три силы:

Р′_y = Р_x/Z = 10/3 = 3,33 кН.

Момент М_R уравновешивают моменты трех сил Р' .каждая из которых направлена перпендикулярно радиусу, проведенному от центра тяжести стыка к центрам сечений болтов. Болты нагружены неодинаково. Наиболее нагруженным является болт 1, воспринимавший наибольшую по величине равнодействующую сил:

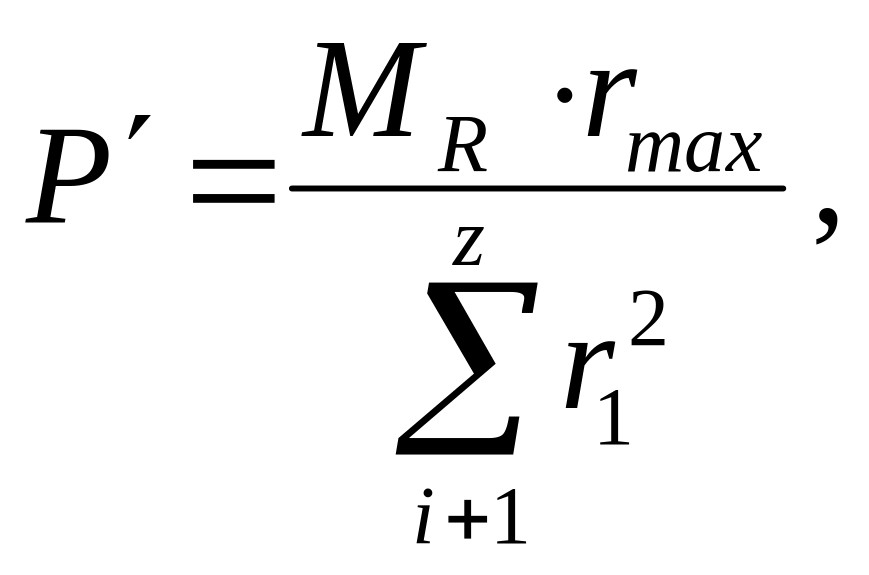
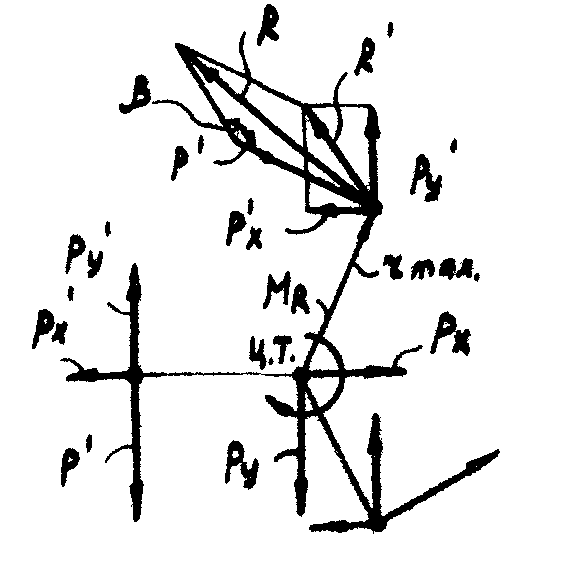
Рис. 6.77

.

.

По схемы сил на рис. 10 определим равнодействующую на болт 1:

.

Используя теорему косинусов получим:

Дальнейшее решение задачи аналогично решению, рассмотренному в примере 8.

Пример 4. Рассчитать болты крепления стального кронштейна к бетонной стене (рис. 6.19). Р₁ = 4 кН, Р₁ = 8 кН; ℓ = 400 мм; h = 300 мм; С = 100 мм; b = 80 мм; Q = 360 мм. Допускаемое напряжение смятия для бетона [σ]_C = 5 МПа. Затяжка болтов контролируемая. Материал болтов сталь 45, [σ] = 240 МПа.

Рис. 6.78. Схема к расчету крепления кронштейна к стене

Решение.

Приводим силы Р₁ и Р₂ к центру тяжести стыка (точки 0). В результате приведения силы Р₁ получаем:

отрывающую силу

S = Р₁ = 4 кН;

опрокидывающий момент

M₁ = Р₁·c = 4·10 = 40 кН·см.

Перенеся силу Р₂ в цент тяжести, получим

сдвигающую силу

Q = Р₂ = 8 кН

опрокидывающий момент

М₂ = Р₂·ℓ = 8·40 = 320 кН·см,

Суммарный опрокидывающий момент

М_с = М₁+ М₂ = 40+320 = 360 кН·см.

Силы, действующие на наиболее нагруженный верхний болт:

от действия силы P₁

Р′₁ = Р₁ /z = 4/2 = 2 кН,

где z – число болтов.

Сила Q стремиться сдвинуть кронштейн вниз, поэтому силы трения в плоскости стыка должны уравновешивать силу Q, т.е.

,

с учетом 20% запаса по сдвигу сила затяжки болта, предотвращавшая сдвиг кронштейна

.

Выбираем коэффициент трения в стыке f = 0,35, тогда сила затяжки болта должна быть

.

Учитывая осевую нагрузку на болт , действительное усилие затяжки

.

Осевая сила, приходящаяся на верхний болт от действия момента

.

Затяжна болтов должна гарантировать не только отсутствие сдвига кронштейна, ни и нераскрытие стыка (не должен появиться зазор в стыке). Определим силу затяжки болта , которая гарантирует нераскрытие стыка. От действия в бетоне на стыке возникают напряжения смятия

,

где F_cm – площадь стыка .

При действии момента М_С напряжение смятия в нижней части стыка возрастает, а в верхней части убывает.

Наибольшее напряжение от момента

.

По условию нераскрытия стыка учетом запаса на нераскрытие стыка

,

где – коэффициент запаса выбираем  = 1,5 [1,§40].

Тогда

.

Сила затяжки болта гарантирующая нераскрытке стыка

.

Учитывая растягивающие усилие , определим действительное усилие затяжки

.

Выбираем коэффициент внешней нагрузки  = 0,2 [1, §40].

Тогда суммарная осевая нагрузка на верхний болт

.

Расчетная нагрузка с учетом скручивания при затяжке

.

Внутренний диаметр резьбы болта

.

По табл.3.3 [5] выбираем болт с ближайшим большим, внутренним диаметром резьбы М 24 (d₁ = 20,753 мм).

Пример 5. Определить диаметр шпилек станочного прихвата (рис. 6.20). Р = 10 кН. Материал основания – сталь Ст. 3, σ_Т = 220 МПа. Затяжка неконтролируемая.

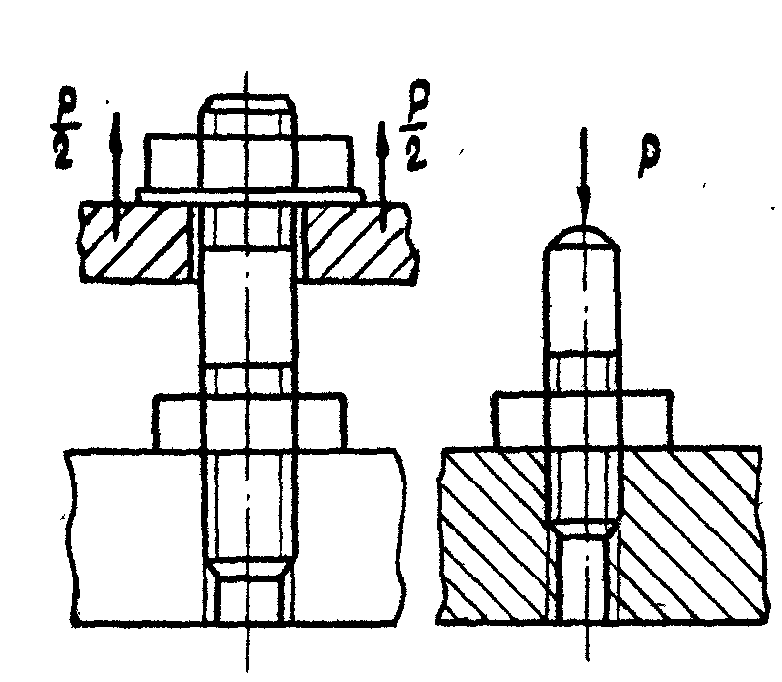
а) б)

Рис. 6.79. Схема к расчету шпилек станочного прихвата

Решение.

Нижняя гайка (рис. 13, а) предназначена для фиксации шпильки; закручивая верхнюю гайку, с помощью планки (1) деталь закрепляется на станке. А в процессе обработки детали шпильки работают в условиях вибрации.

Выбираем материал для шпилек – сталь 45, закаленная, σ_Т = 580 МПа

Выбираем глубину завинчивания шпилек [1,§29]:

h_а = 1,6·d; h_δ = d

Осевая растягивающая сила P_P, действующая на шпильку (рис. 22, а) после предварительной затяжки нижней гайки и приложения внешней нагрузки Р.

,

где влияние скручивания учитывается дважды – при прёдварительной затяжке нижней гайки, а затем верхней – коэффициентом равным 1,3.

Выбираем среднее значение коэффициента внешней нагрузки f = 0,25. Коэффициент затяжки болта, учитывая вибрацию при работе, принимаем К = 2. Условие прочности на растяжение и дополнительное скручивание

.

Коэффициент запаса прочности n при неконтролируемой затяжке и возможной вибрации принимаем n = 6,53, табл.12. [3]

.

Внутренний диаметр резьбы

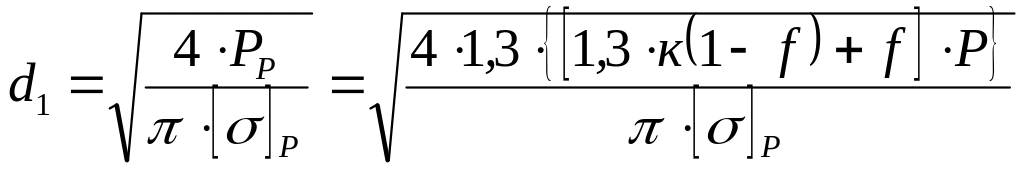
По таблице 3.3 [5] выбираем резьбу М24 (d₁ = 20,752 мм).

Шпилька (рис. 22, б) выполняет функции упора и фиксируется по высоте гайки. Максимальные осевые (сжимавшие) напряжения действуют в сечении по внутреннему диаметру резьбы выше уровня гайки.

Условие прочности

Внутренний диаметр резьбы

По табл. 3.3 [5] выбираем резьбу M14 (d₁ = 12,701 мм)

Замечание.  При проверке резьбы на срез и на смятие расчетная нагрузка выбирается равной внешней силе плюс усилие затяжки фиксирующей гайки. В связи с большим числом витков резьбы, воспринимающих нагрузку (высота гайки плюс глубина завинчивания шпильки), проверку резьбы на срез и на смятие делать нет необходимости.

Пример 6. Рассчитать болты, соединяющие крышку с сосудом для сжатого воздуха (рис. 6.21). Давление воздуха Р = 0,4 МПа; D = 400 мм. Интериал болтов, крышки и сосуда – сталь Ст.3 [σ] = 160 МПа. Затяжка болтов контролируемая.

Рис. 6.80. Схема соединения крышки с сосудом

Решение.

Толщину фланца и крышки для сосуда с диаметром D = 340÷440 мм и давлением Р = 0,2÷0,6 МПа можно выбирать в пределах h₁ = 15÷35 мм Принимаем толщину фланца и крышки h₁ = 30 мм.

Для обеспечения герметичности используем упругую прокладку из капролона (Е₂ = 2·10³ МПа), толщина прокладки h₂ = 1 мм, число болтов [3] Z = 14.

Определяем силу, действующую на болтовое соединение

.

Сила Q_б, приходящаяся на один болт

Q_б = Q/Z = 50265/14 = 3590 Н.

Определяем осевую силу Р₀, действующую на болт после предварительной затяжки и приложения к нему внешней нагрузки [3]

,

где k – коэффициент затяжки, из условия герметичности в соединениях с прокладками принимаем k = 3;

 – коэффициент внешней нагрузки при наличии прокладок принимаем  = 0,6 [3,§25].

Из условия прочности на растяжение внутренний диаметр резьбы

.

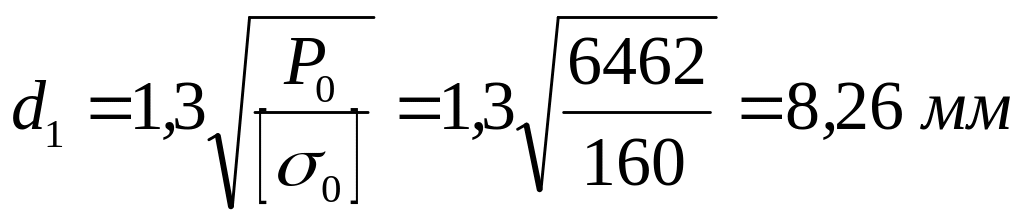По табл.3.3 [5] выбираем болт M10 с внутренним диаметром резьбы d₁ = 6,647 мм и размером под ключ а = 14 мм.

Вычисляем действительное значение коэффициента  и сравниваем его с предварительно принятым значением (= 0,6).

Определяем коэффициент податливости болта

где ℓ – длина болта между головкой и гайкой,

Е – модуль упругости E=210⁵ МПа,

F – площадь поперечного сечения болта.

Диаметр отверстия под болты выбираем d₀ = 10 мм [1].

Определяем коэффициент податливости скрепленных болтами деталей

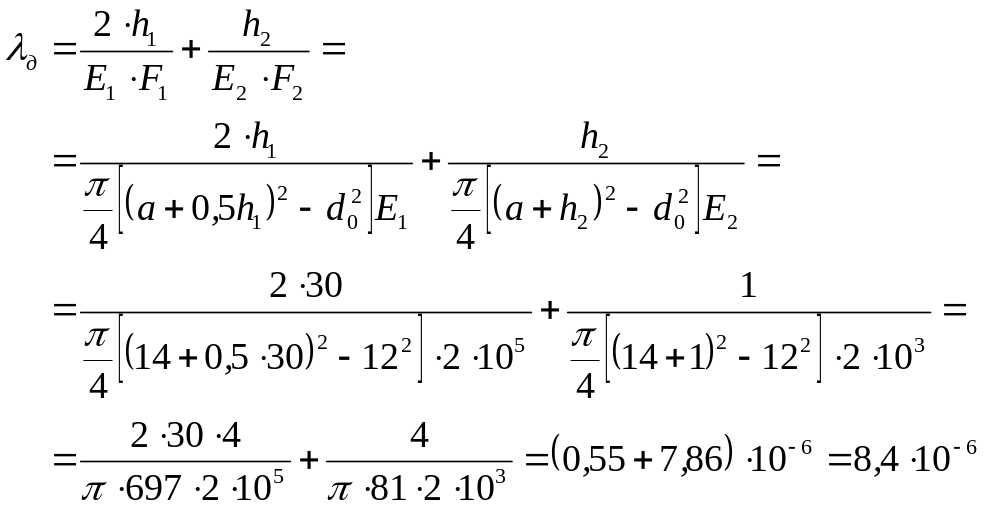
Действительный коэффициент внешней нагрузки

,

что незначительно отличается от ранее принятого значения коэффициента.