Введение

Математическое моделирование - это дисциплина, занимающаяся исследованием систем путем построения и изучения их моделей.

В качестве учебной дисциплины, дисциплина «Математическое моделирование» играет важную роль в подготовке инженеров. Ее значение заключается в том, что на ней базируется любой метод научного исследования, она позволяет освоить методологические и математические средства исследования систем, в том числе, и машиностроительных. От того, насколько профессионально выполнено моделирование, зависит качество принимаемого решения.

Целью данного пособия является приобретение навыков разработки и использования математических моделей для описания, исследования и оптимизации процессов в машиностроении. Основной материал лекций основан на разработках к.т.н., доцента Ивановского государственного энергетического университета Копосова В. Н.

Достижению данной цели служит изучение: 1) общих понятий математического моделирования процессов в машиностроении; 2) теоретических основ математического моделирования и оптимизации процессов в машиностроении; 3) вопросов математического моделирования физических процессов в технологических системах; 4) вопросов математического моделирования и оптимизации технологических станочных систем.

Материал учебного пособия соответствует программе подготовки специалистов по специальности 120100 (151001) «Технология машиностроения». Оно ориентировано главным образом на изучение студентами дисциплины "Математическое моделирование в машиностроении".

Лекция 1 Математическое моделирование силового взаимодействия в зоне резания при изготовлении деталей на станках

Методы расчета сил резания при обработке деталей на металлорежущих станках рассматриваются в курсе «Резание металлов» [2]. Например, для расчета сил резания при точении используются следующие формулы:

где – соответственно, осевая, радиальная и тангенциальная составляющие силы резания

– константы (удельные силы резания), учитывающие влияние на силы резания всех прочих параметров, не входящих в формулы (геометрии инструмента, вида обрабатываемого материала, смазочно - охлаждающей технологической среды (СОТС) и т.д.);

t, s, v - глубина, подача и скорость резания;

x, y, z - показатели степени, выражающие влияние соответствующего параметра режима резания на силы резания;

K_ОБЩ - коэффициент, учитывающий дополнительно влияние на силы резания свойств обрабатываемого, инструментального материала и т.д.

При сверлении для определения силовых параметров используются следующие формулы:

где M_КР, P₀ – соответственно, крутящий момент и осевая сила резания;

C_m, C_p - константы, зависящие от свойств обрабатываемого материала и вида обработки;

D - диаметр обрабатываемого отверстия;

s - подача;

q, y - показатели степени, определяющие степень влияния соответствующего параметра на крутящий момент или осевую силу резания;

K_p - коэффициент, зависящий от свойств обрабатываемого материала.

Представленные уравнения – это уже один из вариантов математической модели процесса точения, сверления с точки зрения действующих сил [10]. Представленная модель может служить для :

1. Описания процесса резания.

2. Исследования процесса резания.

3. Расчета сил резания.

Например, с помощью данной модели можно исследовать зависимость силы резания от глубины резания ( рис.1)

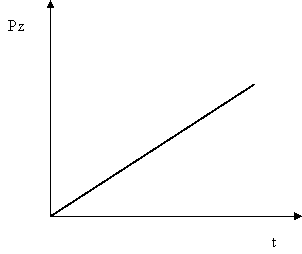
Рис.1. Зависимость силы резания Pz от глубины резания t

Использовать математическую модель процесса резания в таком виде, например, для проведения оптимизации режимов резания нельзя, она слишком проста. Для оптимизации математическая модель должна иметь следующие элементы:

1. Критерий или критерии оптимизации.

2. Целевую функцию.

3. Систему ограничений.

4. Систему уравнений, описывающих объект.

5. Входные, выходные и внутренние параметры.

6. Управляемый (варьируемый) или управляемые (варьируемые) параметры, которые выделяются из числа внутренних параметров.

Пример. Однопараметрическая однокритериальная оптимизация режимов резания.

Пусть требуется определить оптимальную подачу , при этом глубина резания постоянна ( ).

1. Критерий оптимизации - сила резания .

2. Целевая функция – зависимость между критерием (критериями) оптимизации и подлежащими оптимизации параметрами с указанием направления (вида) экстремума. В нашем примере она имеет следующий вид:

3. Система ограничений включает в себя лишь одно из них:

4. Система уравнений. Математическая модель в нашем примере включает в себя одно уравнение

5. Входные параметры –

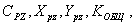
   • выходной параметр –

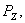
   • внутренние параметры –

6. Управляемый (варьируемый) параметр –

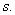
Задача оптимизации решается в два этапа (рис.2):

Этап 1. Определение области допустимости решений (работаем с ограничениями) – ОДР.

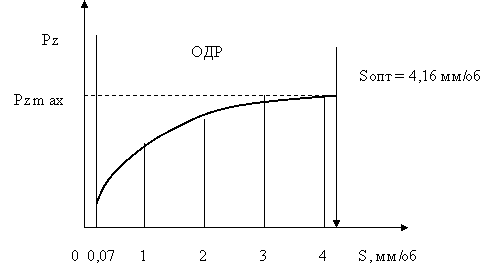Рис. 2. Графическая иллюстрация решения

задачи оптимизации

Этап 2. Определение оптимального параметра –

В общем виде математическая модель объекта записывается:

где – вектор выходных параметров,

– вектор внутренних параметров,

– вектор внешних (входных) параметров,

Для приведенной выше математической модели процесса резания:

Любой объект не может существовать обособленно, без взаимосвязи с другими объектами (окружающей средой). Для процесса резания элементами окружающей среды являются обрабатываемый и инструментальный материалы, смазочно-охлаждающая жидкость, образующаяся в результате обработки стружка и т.д. Для технологического процесса в ходе его реализации- это технологическое оборудование, режущий инструмент, элементы приспособления и т.д. Для технологической системы (механического участка из универсальных станков или станков с ЧПУ, автоматической линии и др.) элементами окружающей среды являются другие технологические системы, цеховой транспорт и т.д.

Структурная схема объекта моделирования представлена на рис.3.

 

Рис.3. Структурная схема объекта моделирования

Эти математические модели используются для практических расчетов. Они получены эмпирическим путем, т.е. на основании проведения экспериментов и обработки их результатов.