
Учебное пособие 800583
.pdf
найти dzdt , выразив предварительно z через t. Имеем
z x2 y3 |
t 2 (t 2 )3 t |
8 , откуда |
dz |
8t 7 , что, безусловно, |
|
dt |
|||||
|
|
|
|
||
совпадает с результатом, полученным по формуле (4.43). |
|||||
Если z |
f (x, y) , |
где y |
|
(x) , то z f (x, (x)) – |
|
сложная функция х. На основании формулы (4.43), в которой
роль t |
играет теперь х, получим |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dz |
|
|
z dx |
|
z |
|
dy |
, а так как |
dx |
1 |
, то |
dz |
|
z |
|
z |
|
dy |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
||||||
|
dx |
x dx |
|
y dx |
|
|
dx |
|
x |
|
y dx |
||||||||||||
|
|
Аналогично решается вопрос |
о |
производной |
сложной |
||||||||||||||||||
функции, когда число промежуточных переменных больше
двух. Например, если u |
f (x, y, z) , где x x(t) , |
y y(t) , |
|||||||||||||
z z(t) , то формула (4.43) принимает вид |
|
||||||||||||||
|
du |
|
u dx |
u dy |
|
u |
|
dz |
. |
(4.44) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dt |
|
x dt |
y dt |
|
z dt |
|
||||||||
Рассмотрим теперь общий случай. Пусть z |
f (x, y) – |
||||||||||||||
функция двух переменных |
х и |
у, которые, в свою очередь, |
|||||||||||||
зависят от двух или большего числа независимых переменных.
Например, пусть |
x x(u, v) , |
y y(u, v) . Тогда функция |
z f x(u, v), y(u, v) |
является сложной функцией независимых |
|
переменных и и v, а переменные х и у – промежуточные.
Если функции |
x(u, v) |
и |
y(u,v) дифференцируемы в |
точке P(u, v) , а функция z |
f (x, y) дифференцируема в точке |
||
M (x, y) , где x x(u, v) , |
y |
y(u, v) , то сложная функция |
|
z f x(u, v), y(u, v) |
дифференцируема в точке P(u, v) , причем |
||
ее частные производные в этой точке находятся по формулам
210

|
|
|
|
z |
|
|
|
|
z |
|
|
x |
z |
|
|
y |
|
, |
|
|
|
|
z |
|
|
|
z |
|
x |
|
|
z |
y |
. |
|
|
|
|
(4.45) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
u |
|
|
|
|
x |
|
|
u |
y |
|
|
u |
|
|
|
|
v |
|
|
|
x |
|
v |
|
|
y |
v |
|
|
|
|
|
|
||||||||||||||||||||||||||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u 2 |
|
|
|
|
|
|
|
|
|
|
|
u 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1. |
Пусть |
|
|
z |
|
|
|
f (x, y) , |
|
x |
|
|
2v, |
|
y |
|
|
|
|
|
. |
По формулам |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|||||
(4.45) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
2u |
|
|
|
z 2u |
, |
|
|
|
|
|
|
z |
|
|
|
|
|
z |
2 |
|
|
z |
|
|
|
u 2 |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
v |
|
|
|
|
|
|
v |
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
v2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2. |
Пусть z |
|
|
x2 y2 , |
x |
|
u |
v , |
y |
|
u |
|
. По формулам (4.45) |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
v |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
z |
|
2xy2 |
1 2x2 y |
1 |
; |
|
|
|
|
|
z |
|
|
|
2xy2 1 2x2 y |
|
|
u |
. |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 |
|
||||||||
Подставьте самостоятельно в эти формулы выражения |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x u |
v , |
y |
|
u |
|
|
|
и, с другой стороны, |
найдите |
|
|
|
z |
|
и |
|
|
z |
, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
v |
|
|
|
|
|
u |
|
|
v |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
предварительно выразив z через и и |
|
|
v, |
|
а затем сравните |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
полученные результаты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3. |
|
|
|
|
|
Пусть |
|
|
z |
|
|
|
x2 |
|
y2 , x |
|
|
|
u cosv, |
|
y |
u sin v . |
|
|
По |
||||||||||||||||||||||||||||||||||||||
формулам (4.45) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
z |
2x cosv 2 y sinv; |
|
|
|
|
z |
|
|
2xusinv 2 yucosv. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
u |
|
|
|
|
v |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Если |
|
|
|
z |
|
|
|
|
|
f (x) , |
где |
|
x |
|
x(u, v) , |
|
то |
|
|
z |
f (x,(u,v)) |
– |
|||||||||||||||||||||||||||||||||||||||||
сложная функция, зависящая через переменную х от двух переменных и и v, и ее частные производные также находятся
по формулам (4.45): |
z |
|
dz |
|
x |
, |
z |
|
dz |
|
x |
. |
|
|
|
|
|
|
|
|
|
||||
|
u |
|
dx |
|
u |
|
v |
|
dx |
|
v |
|
Обратите внимание на обозначения производных в этих формулах.
211
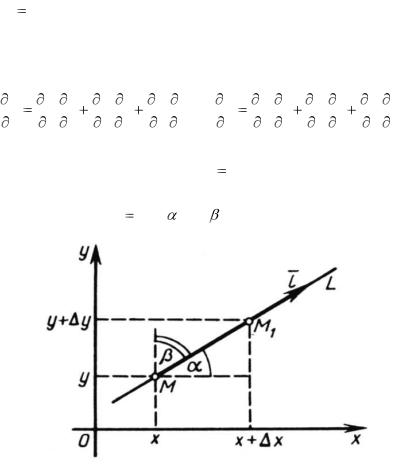
Формулы (4.45) можно обобщить на случай большего числа промежуточных переменных. Например, если
w f (x, y, z) – функция трех переменных х, у, z, а каждая
из них зависит от и и v, то формулы (4.45) принимают вид
|
w w x w y w z |
, |
w |
|
w |
|
x |
|
w |
|
y |
|
w |
|
z |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
u |
|
x u |
y u |
|
z u |
|
v |
|
x v |
|
y v z v |
||||||||||||||||||
|
|
2. Производная по направлению. Градиент. |
||||||||||||||||||||||||||||
|
|
Рассмотрим |
|
|
|
функцию |
z |
|
f (M ) , |
определенную в |
||||||||||||||||||||
некоторой окрестности |
точки |
M (x, y) , |
и произвольный |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
единичный вектор l |
{cos |
|
; cos |
} (рис. 61). |
||||||||||||||||||||||||||
Рис. 61 Для характеристики скорости изменения функции в точке
|
|
|
|
|
M (x, y) |
в направлении вектора l введем понятие производной |
|||
по направлению. Для этого проведем через точку |
М прямую |
|||
L так, |
чтобы одно из направлений на ней |
совпадало с |
||
212

направлением вектора l , и возьмем на направленной прямой
точку M1(x |
x, y |
y) . |
Обозначим величину отрезка |
MM1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
через |
l , |
т.е. |
l |
|
( |
x)2 |
( |
y)2 , если |
точка |
M1 |
||||||
|
|
|
|
|
|
|
|
|
||||||||
расположена так, как на рис.61, и |
l |
|
|
( x)2 |
( y)2 , если |
|||||||||||
точка |
M1 |
расположена |
по |
другую |
|
сторону |
от точки М. |
|||||||||
Функция f (M ) получит при этом приращение |
|
|
|
|
|
|||||||||||
|
|
z f (x |
|
|
x, y |
|
y) |
f (x, y). |
|
|
|
|
|
|||
Определение |
1. |
|
|
Предел |
отношения |
|
z |
при |
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
l |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
l 0 |
(M1 |
M ) , |
если |
|
|
он |
существует, |
называется |
||||||||
производной функции z 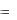 f (M ) в точке M (x, y) по
f (M ) в точке M (x, y) по
|
|
|
|
|
|
|
|
z |
|
lim |
z |
z |
. |
|||
направлению вектора l и обозначается |
, т.е. |
|||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
l |
|
l 0 |
l |
l |
|||
Переходя к пределу в этом равенстве при |
l |
0 , |
||||||||||||||
получаем формулу для производной по направлению |
|
|
|
|
||||||||||||
|
z |
|
|
z |
cos |
z |
cos . |
|
|
(4.46) |
||||||
|
|
|
|
|
|
|
|
|||||||||
|
l |
|
|
x |
y |
|
|
|
|
|
|
|
||||
Из формулы (4.46) следует, что производная по направлению является линейной комбинацией частных производных, причем направляющие косинусы являются как бы весовыми множителями, показывающими вклад в производную по направлению соответствующей частной производной.
В частности, |
z |
|
z |
при |
0 и |
|
; |
z |
|
z |
при |
l |
|
x |
2 |
l |
|
y |
|||||
|
|
|
|
|
|
|
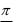 и 0 . Отсюда следует, что частные производные по х
и 0 . Отсюда следует, что частные производные по х
2
и у являются частными случаями производной по направлению.
213
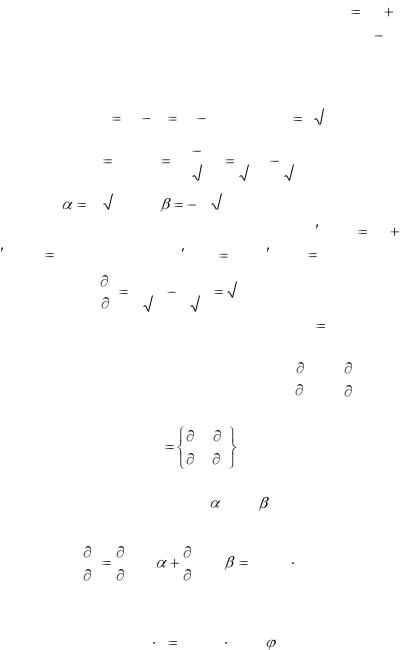
Пример. |
Вычислить производную функции z |
x2 |
|
|
y2x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
||||||
в точке M (1,2) |
по направлению вектора MM1 , |
где |
|
точка |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
с координатами (3,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. Найдем единичный вектор l , имеющий данное |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
направление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
MM1 |
{2; 2} |
|
2i |
|
|
|
|
2 j; |
|
|
|
|
|
|
|
MM1 |
|
|
|
|
2 |
2; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
MM1 |
|
2i |
|
|
|
2 j |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
i |
|
|
|
j, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
MM1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
откуда cos 1/ 2, cos |
|
|
|
|
|
|
1/ |
|
|
|
|
2 . Вычислим частные произ- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
водные |
функции |
|
|
|
в |
точке |
|
|
|
M (1,2) : |
|
f x (x, y) |
2x |
y2 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
f y (x, y) |
2xy, |
|
|
|
|
откуда |
f x (1,2) |
|
|
|
|
6 , f y (1; 2) |
4. |
|
По формуле |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(4.46) получим |
|
|
|
|
z |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
6 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Определение 2. Градиентом функции |
|
z |
|
f (M ) в точке |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M (x, y) называется вектор, координаты |
|
которого |
равны |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
соответствующим частным производным |
|
|
z |
|
|
и |
|
z |
|
, взятым |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
в точке |
M (x, y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Обозначение: grad z |
|
|
|
|
|
|
z |
; |
|
z |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Используя понятие градиента функции и учитывая, что |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
вектор l |
имеет координаты cos |
, |
|
|
cos |
|
|
|
, представим формулу |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(4.46) в виде скалярного произведения векторов grad z |
и |
l |
: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.47) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
cos |
|
|
|
|
|
cos |
|
|
|
|
|
|
|
grad z l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
l |
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
С другой стороны, по определению скалярного |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
произведения имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.48) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
grad z l |
|
|
grad z |
|
|
|
|
l |
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
214

где grad z длина вектора grad z ; 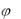 угол между векторами
угол между векторами
l и grad z . Сравнивая формулы (4.47) и (4.48) и учитывая, что
|
|
1, получаем |
z |
|
|
||
l |
grad z |
cos . |
|||||
|
|
||||||
l |
|||||||
|
|
|
|
|
|||
|
|
Из последнего |
равенства следует, что производная |
||||
функции по направлению имеет наибольшую величину при
|
|
|
|
|
|
|
||||
cos 1 ( 0) , т.е. когда направление вектора |
l совпадает с |
|||||||||
направлением grad z . |
При этом |
z |
|
grad z |
|
. Таким образом, |
||||
|
|
|||||||||
|
|
|
||||||||
l |
||||||||||
|
|
|
|
|
|
|
|
|
||
градиент функции z |
f (M ) в точке M (x, y) |
характеризует |
||||||||
направление и величину максимальной скорости возрастания этой функции в данной точке.
Аналогично определяется производная по направлению
для функции трех |
переменных |
|
u f (x, y, z) , |
|
выводится |
||||||||||||
формула |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
u |
cos |
|
u |
cos |
|
u |
cos |
, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
l |
|
x |
y |
z |
|
|
|
|
|
|
||||||
вводится понятие |
|
градиента |
|
grad u |
|
|
u |
; |
|
u |
; |
u |
и |
||||
|
|
|
|
x |
|
y |
z |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
исследуются его свойства.
3. Частные производные высших порядков. Пусть частные производные f x (x, y) и f y (x, y) функции z 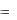 f (M ) ,
f (M ) ,
определенной в окрестности точки М, существуют в каждой точке этой окрестности. В этом случае частные производные представляют собой функции двух переменных х и у, определенные в указанной окрестности точки М. Назовем их
частными производными первого порядка.
В свою очередь, частные производные по переменным х и у от функций f x (x, y) и f y (x, y) в точке М, если они существуют, называются частными производными второго порядка от функции f (M ) в этой точке и обозначаются
215

следующими символами:
2 z |
|
f xx (x, y) |
f (2) |
(x, y); |
|
2 z |
|
f yx (x, y) |
f yx(2) (x, y); |
|
x2 |
|
|
y |
x |
||||||
|
|
x2 |
|
|
|
|
||||
2 z |
|
f yy (x, y) |
f (2) |
(x, y); |
|
2 z |
f xy (x, y) |
f xy(2) (x, y). |
||
y 2 |
|
|
x |
y |
||||||
|
|
y 2 |
|
|
|
|
||||
Частные производные второго порядка вида f yx (x, y) , f xy (x, y) называются смешанными частными производными.
|
|
|
|
|
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1. |
z |
x4 |
4x2 y3 |
|
7xy |
1. Имеем |
|
|
|
|
|
|
|
|||||||||||
|
|
z |
|
4x3 |
8xy3 |
7 y, |
|
z |
|
12x2 y2 |
7x. Следовательно, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
|
y |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 z |
|
12x2 |
8 y3 , |
2 z |
|
|
2 z |
|
24xy2 |
7, |
|
|
|
|
2 z |
24x2 y. |
||||||||
|
|
|
|
x2 |
x |
|
y |
|
|
y |
x |
|
|
|
|
y 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2. |
z |
sin x |
cos y . Имеем, |
z |
cosx cos y, |
|
z |
|
|
sin xsin y. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
x |
|
y |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 z |
|
sin x cos y, |
2 z |
|
|
|
2 z |
|
|
cos x sin y, |
|
|
2 z |
|
|
sin x cos y. |
||||||||||
|
|
x2 |
x y |
|
y |
x |
|
|
|
|
y 2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
В |
обоих |
примерах |
|
смешанные частные производные |
|||||||||||||||||||
|
f yx (x, y) |
и |
f xy (x, y) |
равны. |
Но, |
вообще |
говоря, значения |
|||||||||||||||||||||
смешанных производных зависят от порядка, в котором производится дифференцирование. Так, например, функция
|
xy |
x2 |
y 2 |
при |
x2 |
y 2 |
0, |
|||
f (x, y) |
x |
2 |
y |
2 |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
при |
x2 |
y 2 |
0 |
|
в точке (0; 0) имеет смешанные частные производные f yx (x, y)
216

и f xy (x, y) , но они не равны друг другу. Действительно,
|
|
y(x4 |
y |
4 4x2 y 2 ) |
при |
x2 |
y 2 |
0, |
|||
f x (x, y) |
|
(x2 |
y 2 )2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
при |
x2 |
y 2 |
0. |
Следовательно, |
|
f yx (0,0) |
lim |
|
f x (0,0 |
y) f x (0,0) |
1. |
||||
|
|
|
|
y |
|
||||||
|
|
|
|
y |
|
0 |
|
|
|
|
|
Проводя аналогичные вычисления, получим |
f xy (0,0) 1. |
||||||||||
Таким образом, |
f yx (0,0) |
f xy (0,0). |
|
|
|
|
|||||
Ответ на |
вопрос |
о |
том, |
при каких |
условиях |
значения |
|||||
смешанных производных не зависят от того, в каком порядке производится дифференцирование, дает следующая теорема.
Теорема 2. Если производные f yx (x, y) и f xy (x, y) суще- |
|
ствуют в некоторой |
-окрестности точки M (x, y) и |
непрерывны в самой точке М, то они равны между собой в
этой точке, т.е. имеет место равенство |
f yx (x, y) = f xy (x, y) . |
||
4. Экстремумы функции двух переменных. |
|||
Определение 3. Пусть функция z |
f (x, y) определена в |
||
некоторой окрестности точки |
M 0 (x0 , y0 ) . Говорят, что |
||
функция z |
f (x, y) имеет в точке M 0 |
локальный максимум |
|
(минимум), |
если существует такая окрестность точки M 0 , в |
||
которой для любой точки M (x, y) |
выполняется неравенство |
||
f (x, y) f (x0 , y0 ) ( f (x, y) f (x0 , y0 )). |
|
||
Точки |
локального максимума и локального минимума |
||
называются точками экстремума. Из определения следует, что
если функция |
z |
f (x, y) |
имеет экстремум в точке |
M 0 , то |
|||
полное приращение |
z |
f (M ) |
f (M 0 ) этой функции в точке |
||||
М0 |
удовлетворяет в некоторой окрестности точки |
M 0 |
одному |
||||
из |
следующих |
условий: |
z |
0 (в случае |
локального |
||
217
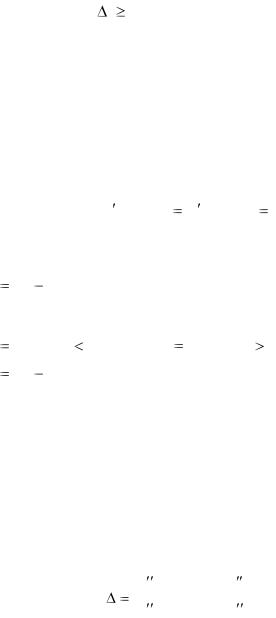
максимума), z 0 (в случае локального минимума). И обратно, если в некоторой окрестности точки M 0 выполняется одно из этих неравенств, то функция имеет экстремум в точке
M 0 .
Теорема 3 (необходимые условия экстремума). Если
функция |
f (x, y) имеет в точке M 0 (x0 , y0 ) экстремум, и в |
||||
точке |
M 0 |
существуют |
частные |
производные |
первого |
порядка, то в этой точке |
частные |
производные |
первого |
||
порядка равны нулю, т.е. |
|
|
|
||
|
|
f x (x0 , y0 ) |
f y (x0 , y0 ) |
0. |
(4.49) |
Условие (4.49) не является достаточным условием |
|||||
экстремума. |
Например, |
частные |
производные |
функции |
|
z x2 |
y2 |
равны нулю в точке (0,0), однако эта функция не |
|||
имеет экстремума в указанной точке, так как равна в ней нулю
и ни в какой окрестности точки (0,0) |
не сохраняет знак: если |
|||||
x |
0 , |
то z |
0 , а если |
y 0 , то |
z |
0 . Графиком функции |
z |
x2 |
y2 является гиперболический параболоид. |
||||
|
Таким |
образом, |
условие |
(4.49) является только |
||
необходимым условием экстремума. Точки, в которых оно выполняется, будем по аналогии с функциями одной переменной называть точками возможного экстремума. Такие точки называются также стационарными.
Теорема 4 (Достаточные условия экстремума). Пусть в точке M 0 (x0 , y0 ) возможного экстремума и некоторой ее
окрестности функция f (x, y) |
имеет непрерывные частные |
|||
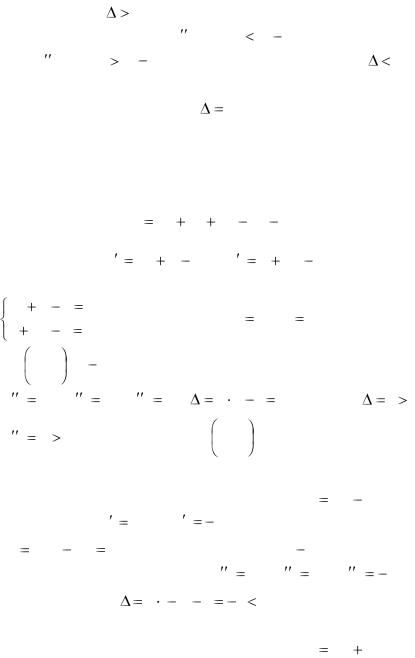
производные второго порядка. Положим |
||||
|
f xx (x0 , y0 ) |
f xy (x0 , y0 ) |
|
. |
|
|
|||
|
f xy (x0 , y0 ) |
f yy (x0 , y0 ) |
|
|
|
|
|
||
Тогда:
218
|
|
а) |
|
если |
|
|
0 , то в точке |
M 0 |
функция |
имеет |
||||||||||||||||
экстремум, причем при |
f xx (x0 , y0 ) |
0 |
локальный максимум, |
|||||||||||||||||||||||
при |
|
f xx (x0 , y0 ) |
0 |
локальный минимум; |
|
б) |
если |
0 , |
то |
|||||||||||||||||
в точке |
|
M 0 |
нет экстремума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
З а м е ч а н и е. Если |
|
0 , |
то функция |
f (x, y) в точке |
||||||||||||||||||||
M 0 |
|
|
возможного |
экстремума |
может иметь |
экстремум, |
но |
|||||||||||||||||||
может и не иметь его. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1. |
Исследовать на экстремум функцию |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
z x2 |
xy y2 |
2x 3y . |
|
|
|
|
|
|
|||||||||
|
|
Имеем, |
|
f x |
2x |
y |
2, |
|
|
f y |
|
x |
2 y |
3. |
Найдем точки |
|||||||||||
возможного экстремума. |
|
Для этого решим систему уравнений |
||||||||||||||||||||||||
2x |
|
y |
2 |
0, |
решения которой x |
|
1 |
, y |
|
4 |
. Следовательно, |
|||||||||||||||
x |
2 y |
3 |
0, |
3 |
3 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
M 0 |
|
1 |
; |
4 |
|
|
|
точка |
возможного |
экстремума. |
Далее, |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f xx |
|
2, f xy |
|
1, |
f yy 2, |
|
|
2 |
2 |
1 |
3. Так как |
3 |
0 и |
|||||||||||||
f xx |
2 |
0, |
то |
в |
точке |
M 0 |
1 |
; |
4 |
|
|
данная функция имеет |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|||
минимум. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2. Исследовать на экстремум функцию z |
x2 |
y2 . |
|
|||||||||||||||||||||
|
|
Имеем |
|
f x |
|
2x, |
f y |
|
2 y . |
Решая систему уравнений |
||||||||||||||||
2x |
0 , |
|
2y |
0 , получаем, |
что M 0 (0,0) |
|
точка возможного |
|||||||||||||||||||
экстремума. |
|
Так |
как |
|
f xx |
2, |
f xy |
0, |
f yy |
2 |
и, |
|||||||||||||||
следовательно, |
|
|
2 ( |
2) |
0 |
|
|
4 |
|
0 , то |
в точке |
M 0 (0,0) |
||||||||||||||
экстремума нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3. Исследовать на экстремум функцию z |
x4 |
y4 . |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
219 |
|
|
|
|
|
|
|
|
|
|
||||
