
Учебное пособие 800583
.pdf
В общем случае множество образов элементов из Χ, отображаемых в Υ, является подмножеством множества Υ: f (X ) Y .
В том случае, когда Υ есть в точности множество всех
значений f (x) для x из Χ, т.е. когда f (X ) |
Y , |
говорят, что |
f есть функция, отображающая Χ на Υ. |
|
|
Итак, в общем случае нельзя полагать, |
что |
f задается |
формулой, из которой можно найти область определения и множество значений функции. Кроме того, Χ и Υ не
обязательно являются множествами |
R n , |
R m , или |
|
подмножествами этих множеств. |
|
|
|
Рассмотрим несколько хорошо знакомых читателю |
|||
примеров геометрически определенных функций. |
|
||
Параллельный перенос плоскости |
есть |
функция |
|
f : R2 |
R2 (где R2 множество упорядоченных пар ( x, y ), т.е. |
||
множество точек плоскости). Эта функция определяется как результат поступательного движения плоскости, рассматриваемой как плоское тело, при котором каждая точка пробегает прямолинейный отрезок или вектор. Все векторы, являющиеся траекториями различных точек, параллельны, имеют одну и ту же длину и одно и то же направление. Перенос задается таким вектором для какой-либо одной точки; все другие векторы можно по нему построить.
Например, если известно, |
что f |
переводит точку |
M1 |
в |
||
точку |
M 2 , то это отображение будет переводить точку |
M1 |
в |
|||
такую |
точку M 2 , что точки |
M1 , |
M 2 , M1 , |
M 2 |
будут |
|
составлять параллелограмм. |
|
|
|
|
|
|
Вращение плоскости есть функция f : R2 |
R2 , которая |
|||||
также определяется как результат движения плоскости, рассматриваемой как твердое тело, но в этом случае –
160

вращения её вокруг неподвижной точки M 0 , называемой центром вращения.
Каждая окружность с центром в точке M 0 переводится отображением f в себя, а каждая полупрямая с началом в M 0
, переводится в другую полупрямую. Угол, образованный этими двумя лучами, называется углом вращения. Его величина не зависит от исходного луча. Вращение вполне определяется центром и углом поворота.
Отражение относительно прямой L в |
R2 - функция |
f : R2 R2 . Она оставляет неподвижной |
каждую точку |
прямой L и меняет местами две полуплоскости, на которые прямая L разбивает плоскость. Отражение можно представить
себе как результат вращения плоскости в пространстве R 3 вокруг прямой L на 180˚.
В геометрии доказано, что любое движение плоскости, рассматриваемой как твердое тело, которое переводит эту плоскость в себя, есть параллельный перенос, вращение, отражение или отражение со следующим за ним параллельным переносом. Форма и размеры фигур на плоскости при таких отображениях f не меняются. Могут измениться лишь их
положение и ориентация. Эти функции представляют движения, рассматриваемые в элементарной геометрии.
Подобие плоскости есть функция |
f : R2 |
R2 , |
изменяющая длины всех отрезков в одно и то же число раз r .
Например, выберем точку M 0 из R2 , положим |
f (M 0 ) M 0 , |
а для каждой другой точки М в качестве f (M ) |
возьмем конец |
вектора, начинающего в точке M 0 , имеющего направление
M 0 M и удвоенную длину. Такая функция увеличивает все длины в два раза.
161

Такого рода функции f при r 1 называются
растяжением, а при r 1 сжатием с центром в M 0 .
Подобие всегда переводит прямые линии в прямые линии и не меняет величины углов между ними. Это преобразование изменяет размеры, положение и ориентацию произвольной фигуры, но не изменяет ее формы.
Важным классом отображений являются биективные, т.е.
взаимно однозначные отображения. |
|
|
||
Функция F : X |
Y |
называется |
взаимно |
однозначной |
(сокращенно 1 – 1 функцией), если каждая точка |
y множества |
|||
Υ является образом |
при f |
одной и |
только одной точки x |
|
множества Χ.
В этом случае функция, ставящая в соответствие каждой
точке y |
Y единственную точку x |
X , |
для которой f (x) |
y , |
|||
называется обратной |
функцией |
для |
f |
и обозначается |
|||
f 1 : Y |
X . |
|
|
|
|
|
|
Например, каждое движение плоскости взаимно |
|||||||
однозначно. Если f |
– параллельный |
перенос, |
задаваемый |
||||
прямолинейным отрезком, идущим из |
M 0 |
в М, |
то f |
1 – |
|||
параллельный перенос, задаваемый параллельным отрезком, идущим из М в M 0 .
Функция, обратная вращению, является вращением с тем же центром и с углом, равным по величине, но противоположным по знаку. Подобие плоскости также взаимно
однозначно. |
Отображение, |
обратное |
растяжению |
с |
|||
коэффициентом |
r |
1 , есть сжатие с коэффициентом |
1 |
и с |
|||
r |
|||||||
|
|
|
|
|
|
||
тем же центром. |
|
|
|
|
|
||
Если f – отображение множества Χ |
на множество Υ, а |
||||||
g – отображение множества Υ |
в множество Z , то для x |
X |
|||||
определен элемент |
y f (x) Y |
и можно рассмотреть элемент |
|||||
162
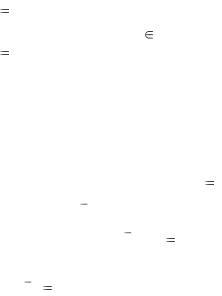
z g( y) , |
принадлежащий |
множеству Z . Таким образом, |
|||||||
каждому |
элементу |
x |
X |
ставится |
в соответствие элемент |
||||
z |
g[ f (x)] из |
Z |
и, следовательно, |
определено отображение |
|||||
множества Χ в множество Z, называемое композицией |
|||||||||
отображений |
f и g |
или сложной функцией, и обозначаемое |
|||||||
g f (x) или g[ f (x)]. |
|
|
|
|
|
||||
|
В общем |
случае |
композиция |
не коммутативна: g f |
|||||
отличается от |
f g , |
если даже последняя имеет смысл; но |
|||||||
она ассоциативна – (h g) f |
h (g f ) . |
|
|||||||
|
Если |
f 1 есть биекция, |
обратная биекции |
f множества |
|||||
Χ |
на Υ, |
то |
f |
1 f |
I x |
– тождественное |
отображение |
||
множества Χ; перестановка отображений в композиции дает f f 1 I y – тождественное отображение множества Υ.
4.4. Предел функции нескольких переменных
Далее в этой главе мы будем рассматривать функции двух и трех переменных, значения которых будут являться вещественными числами, то есть область их значений будет
подмножеством множества R1 или совпадать с R1 . Введенные в п. 4.1 понятия открытых и замкнутых областей, а также окрестностей точек, будут использоваться при определении понятий предела и непрерывности функции.
1. Предел последовательности точек.
Введем предварительное понятие последовательности точек n-мерного евклидова пространства. Пусть каждому числу m натурального ряда чисел 1,2,…,m,… ставится в
соответствие |
точка |
M m |
евклидова |
пространства |
E n . |
Возникающий |
при |
этом |
ряд точек |
M1 , M 2 ,..., M m ,…, |
|
рассматриваемый в |
указанном порядке, называется |
||||
163

последовательностью точек евклидова |
пространства |
E n и |
|||||
обозначается символом {M m } . |
|
|
|
|
|||
Определение. |
Последовательность |
{M m } |
точек |
||||
евклидова пространства |
E n |
называется |
сходящейся, если |
||||
существует точка |
M 0 |
пространства |
E n такая, что для |
||||
любого положительного числа |
можно указать отвечающий |
||||||
ему номер N такой, что при m |
N выполняется неравенство |
||||||
(M m , M 0 ) |
. При этом точка M 0 |
называется пределом |
|||||
последовательности {M m } .
Для обозначения предела последовательности используют
символы: |
|
|
|
|
|
|
lim M m |
M 0 , или |
M m |
M 0 |
при m |
. |
|
m |
|
|
|
|
|
|
Справедливо важное утверждение, сводящее сходимость |
||||||
последовательности |
точек |
{M m } |
к |
покоординатной |
||
сходимости. |
|
|
|
|
|
|
Теорема 1. Последовательность точек {M m } n- мерного |
||||||
евклидова пространства E n |
сходится |
к |
точке |
M 0 этого |
||
пространства тогда и только тогда, когда числовые последовательности координат точек M m { x1m }, { x2m },…, {
xnm } сходятся соответственно |
к числам x10 ,..., xn0 , |
||||
представляющим координаты точки |
M 0 . |
||||
Пример. Пусть последовательность точек { M n (xn , yn ) } |
|||||
из R 2 такова, что |
|
|
|
|
|
xn |
1 |
, yn |
3 |
, n |
1,2... . |
|
|
||||
|
n |
n |
|
||
164

Тогда пределом последовательности точек M n |
1 |
, |
3 |
|||||||
n |
n |
|||||||||
|
|
|
|
|
|
|
|
|||
при n |
, будет, очевидно, точка |
O(0,0) : |
|
|
|
|||||
|
lim M n |
1 |
, |
3 |
|
O(0,0) . |
|
|
|
|
|
|
n |
|
|
|
|||||
|
n |
n |
|
|
|
|
||||
2. Предел функции.
Рассмотрим функцию u 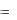 f (M ) , определенную на множестве {M} точек n-мерного евклидова пространства E n
f (M ) , определенную на множестве {M} точек n-мерного евклидова пространства E n
и точку А пространства E n , быть может и не принадлежащую множеству {M}, но обладающую тем свойством, что в любой - окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от точки А (такая точка называется
предельной точкой множества {M}).
Определение 1. (Предел функции в точке А по Гейне).
Число b называется пределом (или предельным
значением) функции u |
f (M ) |
в точке А ( или при M A ), |
если для любой сходящейся к |
А последовательности { M m } |
|
точек множества {M} задания этой функции, все элементы |
||
которой M m отличны |
от А, соответствующая числовая |
|
последовательность значений функции { f (M m ) } сходится к числу b.
Для обозначения предела функции u f (M ) |
в точке А |
|||
используются обозначения: |
|
|
|
|
lim f (M ) b или |
|
lim f (x1,...., xn ) |
b , |
|
M A |
x1 |
.... |
a1 |
|
|
|
|
|
|
|
xn |
an |
|
|
где a1, …, an - координаты точки А.
Определение 2. (Предел |
функции в точке А по Коши). |
|
Число b называется |
пределом (или предельным |
|
значением) функции u f (M ) в точке А (или при M |
A ), |
|
165
если |
для |
любого |
положительного |
числа |
|
|
найдется |
||||||||||||||
отвечающее ему положительное |
число |
|
|
такое, что |
для |
||||||||||||||||
любой точки М из множества {M} задания этой функции, |
|||||||||||||||||||||
удовлетворяющей |
условию |
0 |
(M, A) |
, |
справедливо |
||||||||||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
неравенство |
f (M ) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
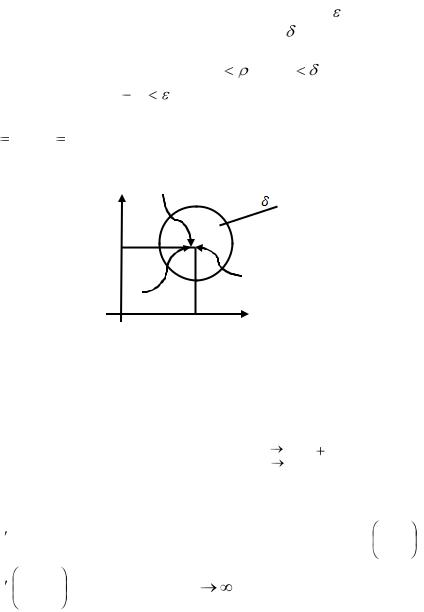
З а м е ч а н и е. Согласно определению, предел функции |
||||||||||||||||||||
u f (M ) |
f (x, y) |
не зависит от способа приближения точки |
|||||||||||||||||||
M (x, y) |
к точке A(a,b) |
(рис. 52). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y |
(2) |
|
|
-окрестность точки А. |
||||||||||||
|
|
|
|
|
b |
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
M(x,y) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
a |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Предел должен быть одним и тем же числом b при |
||||||||||||||||||||
приближении точки M (x, y) |
к точке |
A(a,b) |
по любому пути. |
||||||||||||||||||
|
Пример 1. Существует ли предел |
lim |
|
2xy |
? |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
y 2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
0 x2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
Решение. Воспользуемся определением 1 предела |
||||||||||||||||||||
функции. Возьмем две последовательности точек { M n } |
и { |
||||||||||||||||||||
M n }, |
сходящиеся |
к |
точке О(0,0). |
Пусть |
|
M n |
|
1 |
, |
1 |
, |
||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
||
M n |
1 |
, |
1 |
|
которые |
при |
n |
приближаются |
к |
О(0,0). |
|||||||||||
|
n2 |
|
|||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получаем |
|
две |
|
|
соответствующие |
|
|
этим |
|
точкам |
|||||||||||
последовательности значений функций |
|
|
|
|
|
|
|
|
|
|
|||||||||||
166

|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xn , yn ) |
n2 |
1 |
, |
f (xn , yn ) |
|
n3 |
|
|
|
2 |
|
0 |
(при |
||||
2 |
1 |
1 |
|
|
n |
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
n2 |
|
|
n4 |
|
n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
рассматриваемый предел не существует. |
|||||||||||||||
Этот результат можно получить другим способом, устремляя точку M (x, y) к точке О(0,0) по прямой y kx . Действительно,
f (x, kx) |
2kx2 |
|
2k |
|
|
|
|
. |
|
x2 k 2 x2 |
1 k 2 |
|||
Таким образом, приближаясь к точке О(0,0) по разным прямым, соответствующим разным значениям углового коэффициента k , получаем разные предельные значения функции. Отсюда и следует, что предел этой функции в точке О(0,0) не существует.
Пример 2. Существует ли предел |
lim |
|
|
x2 y |
|
? |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 x2 y |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
||
Решение. Выполним оценку абсолютной величины |
|||||||||||||||||||||||||||
функции. Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x |
2 |
y |
|
|
|
|
|
|
|
x |
|
2xy |
|
1 |
|
x |
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x2 |
|
y 2 |
2 |
|
x2 |
y 2 |
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Выполнение последнего неравенства легко увидеть из |
|||||||||||||||||||||||||||
рассуждений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2xy |
|
1 , |
|
2 |
|
xy |
|
x 2 |
y 2 , |
|
(x y)2 |
|
0 . |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x 2 |
y 2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y |
|
|
|
|||||
Поскольку lim |
|
x |
|
0 , |
|
то |
lim |
|
|
|
0 . |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
2 |
|
|
|
x2 |
|
|
y2 |
|
|||||||||||||||||||
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
167

Пример 3. Существует ли предел lim |
x 2 y |
? |
|||
x 4 |
y 2 |
||||
x |
0 |
|
|||
y |
0 |
|
|
|
|
Решение. Данная функция определена во всех точках |
|||||
плоскости, то есть пространства R 2 , |
кроме точки О(0,0). |
||||
Вычислим предел этой функции при (x, y) |
(0,0) по любой |
||||
прямой y kx , проходящей через начало координат. Имеем:
f (x, kx) |
|
kx3 |
|
|
kx |
|
0 |
при x |
0. |
|
||||
x4 k 2 x2 |
x2 |
k 2 |
|
|||||||||||
|
|
|
|
|
|
|
||||||||
Однако эта функция не имеет предела в точке (0,0), |
||||||||||||||
поскольку при y |
x2 , получаем: |
|
|
|
|
|
|
|||||||
f (x, x2 ) |
|
x4 |
|
1 |
, |
поэтому lim f (x, x2 ) |
|
1 |
. |
|||||
x4 |
x4 |
2 |
2 |
|||||||||||
|
|
|
|
x |
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
y |
x 2 |
|
|
|
|
Введем понятие предела функции u 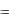 f (M ) при M
f (M ) при M  . Для этого надо считать, что множество {M}, на котором задана
. Для этого надо считать, что множество {M}, на котором задана
эта функция, для любого |
|
0 имеет хотя бы один элемент М, |
||||||||
лежащий вне шара радиуса |
|
с центром в точке О(0,…,0). |
||||||||
Определение. |
Число |
b |
называется |
пределом функции |
||||||
u f (M ) |
при |
M |
, |
если для |
любого положительного |
|||||
числа |
найдется отвечающее ему положительное число |
|||||||||
такое, что для всех точек М из множества {M} задания |
||||||||||
функции, |
удовлетворяющих условию |
(O, M ) |
, справедливо |
|||||||
|
|
|
|
|
|
|
||||
неравенство |
f (M ) b |
|
. |
|
|
|
|
|||
Для обозначения предела функции u |
f (M ) |
при M |
||||||||
используется символ: |
|
|
|
|
|
|||||
|
|
|
|
|
lim |
f (M ) |
b . |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
Как и в случае функции одной переменной, |
||||||||||
арифметические |
операции |
над |
функциями |
нескольких |
||||||
168

переменных, имеющими предел в данной точке M 0 |
(или при |
||||
M |
) , приводят к функциям, |
имеющим предел в точке M 0 |
|||
(соответственно при |
M |
). |
|
|
|
|
Теорема 2. |
Пусть |
две |
функции f1(M ) и |
f2 (M ) |
определены на одном и том же множестве и имеют в точке
M 0 пределы |
b1 и |
b2 . |
Тогда |
функции |
f1(M ) |
f2 (M ) , |
||
f1(M ) f2 (M ) , |
f1(M ) / f2 (M ) |
имеют в точке M 0 |
пределы, |
|||||
равные соответственно |
b1 |
b2 , |
b1 b2 , b1 / b2 |
(в |
случае |
|||
частного нужно дополнительно требовать, чтобы b2 |
0 . |
|||||||
Доказательство |
этих |
утверждений |
совершенно |
|||||
аналогично доказательству подобной теоремы для функций одной переменной.
Пример 4. Вычислить предел |
|
|
lim |
x |
2 y |
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
3x |
|
y |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Согласно сформулированной |
выше |
|
теореме, |
|||||||||||||||||||||||||
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim x |
|
|
||
|
|
x |
2 y |
|
|
x |
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
lim |
lim |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|||||||||
3x |
y |
3x |
y |
3x |
y |
|
3 lim x lim y |
||||||||||||||||||||||
x |
1 |
x |
1 |
x |
1 |
|
|||||||||||||||||||||||
y |
2 |
|
|
y |
2 |
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
x |
1 |
|
x |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
y |
2 |
|
|||
|
|
|
|
|
|
2 lim y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
1 |
|
|
4 |
|
|
|
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||
|
|
|
|
|
3 lim x |
|
lim y |
|
5 |
|
5 |
|
5 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
x |
1 |
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5. Вычислить предел |
lim |
|
|
|
|
|
|
x |
|
y |
|
. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x 2 |
|
|
|
|
|
|
y 2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
xy |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
169
