
Учебное пособие 800583
.pdf
Определение. Пусть функция f (x) определена на промежутке [a, ) и интегрируема по любому отрезку a, R ,
R
т. е. существует определенный интеграл |
f (x) dx при любом |
|
|
|
a |
R a . Тогда, если существует конечный предел |
||
|
R |
|
lim |
f (x) dx, |
(3.19) |
R |
a |
|
|
|
|
то его называют несобственным интегралом первого рода и обозначают
f (x) dx. (3.20)
a
Таким образом, по определению,
|
|
R |
f (x) dx |
lim |
f (x) dx. |
a |
R |
a |
|
В этом случае говорят, что интеграл (3.20) существует или сходится. Если же предел (3.19) не существует или бесконечен, то говорят, что интеграл (3.20) не существует или расходится.
Аналогично интегралу (3.20) вводится несобственный интеграл по промежутку 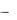 , b :
, b :
b b
f (x) dx |
lim |
f (x) dx. |
|
(3.21) |
R |
R |
|
|
|
|
|
|
|
|
Наконец, как сумму интегралов вида (3.20) |
и |
(3.21) |
||
можно определить несобственный |
интеграл |
с |
двумя |
|
бесконечными пределами, т. е. |
|
|
|
|
120

|
c |
|
|
f (x) dx |
f (x) dx |
f (x) dx, |
(3.22) |
c
где с – любое число, при условии существования обоих интегралов справа.
Установим геометрический |
смысл |
несобственного |
|||
интеграла первого рода. Пусть |
f (x) |
0. |
Тогда определенный |
||
|
R |
|
|
|
|
интеграл |
f (x)dx выражает площадь области, ограниченной |
||||
|
a |
|
|
|
|
сверху графиком функции f (x) , снизу – |
осью Ох, слева – |
||||
прямой x |
a , справа – прямой |
x |
R . Естественно считать, |
||
что несобственный интеграл |
f (x)dx |
выражает конечную |
|||
|
|
a |
|
|
|
площадь бесконечной области, ограниченной сверху графиком функции f (x) , снизу осью Ох, слева прямой x a . Аналогичная интерпретация имеет место для интегралов (3.21)
и (3.22). |
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
|
несколько |
примеров |
вычисления |
||||||||
несобственных интегралов первого рода. |
|
|
|
|
||||||||
Пример 1. |
|
|
|
|
|
|
|
|
|
|
||
|
dx |
|
R |
dx |
|
|
|
0R |
|
|
|
|
|
Rlim |
|
Rlim |
(arctg x) |
|
Rlim arctg R |
|
, |
||||
|
|
|
|
|||||||||
|
2 |
|
2 |
2 |
||||||||
0 1 x |
|
0 1 x |
|
|
|
|
|
|
|
|
||
т.е. данный интеграл сходится.
Пример 2.
|
|
R |
|
|
0R |
cos x dx |
lim |
cos x dx |
lim sin x |
|
|
|
|||||
0 |
R |
0 |
R |
|
|
|
|
|
|
||
но предел функции |
sin R |
при R |
|
|
|
следовательно, интеграл расходится. |
|
|
|||
lim sin R,
R 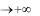
не существует,
121

|
|
0 |
|
|
Пример 3. |
e x dx |
e x dx |
e x dx; |
интеграл |
|
|
|
0 |
|
расходится, так как
|
|
R |
|
|
|
|
R |
|
|
|
|
e x dx lim |
|
|
e x dx |
lim e x |
|
lim (e R 1) |
. |
||
0 |
R |
0 |
|
R |
|
|
0 |
R |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||
|
Пример 4. |
|
|
dx |
, |
некоторое число. |
|
|||
|
|
|
|
|
||||||
1x
1)Если 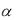 1, то для любого R > 0
1, то для любого R > 0
|
R dx |
|
|
x1 |
|
R |
|
|
R1 |
1 |
1 |
при |
1, |
||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
lim |
|
|
lim |
|
|
|
|
lim |
|
|
1 |
|
|
|
R |
x |
R |
1 |
|
1 |
R |
1 |
|
при |
1. |
|||||
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) Если |
1, |
то для любого R > 0 |
|
|
||||||
|
lim |
R dx |
lim (ln x) |
|
1R |
lim |
ln R |
. |
||
|
|
|||||||||
|
|
|
x |
|||||||
|
R |
1 |
|
R |
|
|
R |
|
|
|
Таким образом, |
данный интеграл сходится при |
1 и |
||||||||
расходится |
при |
|
1. Заметим, |
что в |
рассмотренных |
|||||
примерах вычисление несобственного интеграла было основано на его определении.
2. Несобственные интегралы от неограниченных функций.
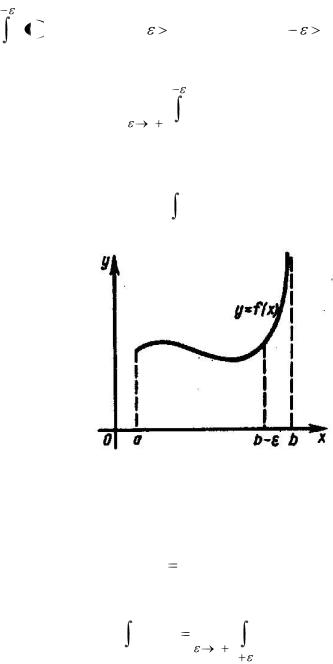
Определение. Пусть функция f (x) определена на промежутке a, b . Точку x b будем называть особой, если функция f (x) неограничена в любой окрестности этой
точки, но ограничена на любом отрезке a, b |
, заключенном |
в a, b (рис. 39). Пусть на любом отрезке a, b |
функция |
f (x) интегрируема, т. е. существует определенный интеграл
122
b
f x dx при любом |
0 таком, что b |
a. Тогда, если |
a
существует конечный предел
|
b |
|
lim |
f (x)dx, |
(3.23) |
0
a
то его называют несобственным интегралом второго рода и обозначают
b
f (x)dx. |
(3.24) |
a
Рис. 39
В этом случае говорят, что интеграл (3.24) существует или сходится. Если же предел (3.23) не существует или бесконечен, то говорят, что интеграл (3.24) не существует или расходится.
Аналогично, если x a – особая точка, то несобственный интеграл определяется так:
b b
f (x)dx |
lim |
f (x)dx. |
a |
0 |
a |
123

Если функция f (x) не ограничена в окрестности какойнибудь внутренней точки с a, b , то при условии
существования обоих интегралов справа по определению полагают
b |
c |
b |
f (x)dx |
f (x)dx |
f (x)dx. |
a |
a |
c |
Наконец, если a и b – особые точки, то если оба интеграла справа существуют, несобственный интеграл определяется как сумма
|
|
|
b |
|
c |
|
|
|
b |
|
|
|||||
|
|
|
|
f (x)dx |
f (x)dx |
|
f (x)dx, |
|
|
|||||||
|
|
|
a |
|
a |
|
|
|
c |
|
|
|||||
где c – любая точка из |
(a,b) . |
|
|
|
|
|
|
|
|
|||||||
Пример 5. |
1 |
dx |
, |
0 |
|
|
некоторое число. |
|
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
0 x |
|
|
|
|
|
|
|
|
|
|
||
1) |
|
Если |
1, |
то |
|
|
|
|
|
|
|
|
||||
1 |
dx |
|
|
x1 |
|
1 |
|
1 |
1 |
|
|
|
при |
1, |
||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||
lim |
|
lim |
|
|
|
|
|
lim |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
при 0 |
1. |
||||||
0 |
x |
0 |
|
|
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2)Если 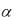 1, то
1, то
lim |
1 dx |
lim (ln x) |
|
1 |
lim ( ln ) |
. |
|
|
|
|
|||||||
|
x |
|
||||||
0 |
|
0 |
|
|
0 |
0 |
1 |
|
Таким образом, данный интеграл сходится при |
||||||||
ирасходится при 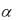 1.
1.
3.Пример использования несобственного интеграла.
Вычислим вторую космическую скорость тела, т.е. начальную скорость, при которой оно способно выйти из поля притяжения Земли в межпланетное пространство.
124

Ранее с помощью определенного интеграла была вычислена работа, необходимая для запуска тела массой m с поверхности Земли на высоту h
|
|
|
R h |
|
|
|
PRh |
|
|
||||
|
|
A |
|
F (x) dx |
|
. |
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
R |
|
|
|
|
|
R |
h |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выход тела в межпланетное пространство означает запуск |
|||||||||||||
его на бесконечную высоту |
h |
|
. Вычислим необходимую |
||||||||||
для этого работу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim A |
F (x) dx |
|
lim |
|
PRh |
lim |
|
|
PR |
PR mgR, |
|||
|
|
|
|
|
|
|
|
||||||
|
|
R |
h |
1 R / h |
|||||||||
h |
R |
h |
|
|
h |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где m – масса тела; g – ускорение свободного падения у поверхности Земли (трение и притяжение других планет при этом не учитываются). Эта работа совершается за счет изменения кинетической энергии тела. Поэтому кинетическая энергия тела в начальный момент должна быть не меньше этой работы, т.е. начальная скорость тела v должна быть такая,
чтобы |
|
mv |
2 |
|
mgh или |
||
|
|
|
|
|
|||
2 |
|
||||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
v |
2gR |
|
|
2 10 6 400 000 м с 1,4 8 000 м с 11,2 км с. |
|||
Если начальная скорость тела равна 11,2 км/с, то его траектория движения представляет собой параболу. При начальной скорости, большей 11,2 км/с, траектория будет представлять собой гиперболу, а при начальной скорости, меньшей 11,2 км/с, тело будет двигаться по эллиптической траектории. При этом либо упадет на Землю, либо станет искусственным спутником Земли.
125

Задачи к п. 3
b
1. xn dx (n 1). a
1
5. (
 x x 2 )dx.
x x 2 )dx.
0
/2
8.cos xdx.
|
0 |
|
|
||
0 |
|
3x4 |
3x2 1 |
||
|
|
||||
|
|
|
|
dx. |
|
/ 4 |
1 |
x2 |
|||
|
|||||
|
|
|
|||
2
14. x 3 x dx.
0
e
17.ln xdx.
1

 3
3
20.arctg xdx.
|
0 |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
23. |
x2 |
|
a2 x2 dx. |
|||||
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
26. |
|
|
x |
dx. |
||||
|
|
|
||||||
|
|
|
|
|||||
|
|
|
||||||
|
0 |
|
x |
1 |
|
|||
|
|
|
|
|
|
|
|
|
2
2. (3x2 1)dx.
0
6.sin xdx.
0
1 |
|
|
dx |
|
|
9. |
|
|
. |
||
1 |
x2 |
||||
0 |
|
||||
|
|
|
|
||
2
12. x 2 1 dx.
1 x 4
3. |
2 |
dx |
. |
|
4. |
2 e x dx. |
|||||
|
|
|
|||||||||
|
1 |
|
x |
|
|
|
|
1 |
|||
|
3 |
|
|
dx |
|
|
|
|
|
||
7. |
|
|
|
|
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
0 |
1 |
x 2 |
|
|
||||||
|
|
|
/ 4 |
|
x2 |
|
|
||||
10. |
|
|
|
|
|
dx. 11. |
|||||
0 |
1 x2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
1
dx
13.  .
.
0  4 x 2
4 x 2
3
15.sin 2dx.
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
dx |
|
|
|||
18. |
|
|
|
. |
|||||
|
|
|
|
|
|
|
|||
|
x 2 |
|
2x 2 |
||||||
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
1 |
|
x2 dx. |
|
|
||||
21. |
|
xe |
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
/ 2 |
|
|
dx |
|
|
||
24. |
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|||
|
0 |
2 |
cos x |
||||||
|
1/ 2 |
|
|
|
|
|
|||
27. |
1 |
x |
|
dx. |
|||||
|
|
|
|
|
|||||
|
|
0 |
1 |
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
16.x sin xdx.
2
e
19.ln2 xdx.
1
1
22.x 2e x dx.
1 |
|
|
|
|
|
|
|
|
|
4 |
|
|
dx |
|
|
|
|
|
|
25. |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||
0 1 |
|
|
x |
|
|||||
4 |
|
|
dx |
|
|||||
28. |
|
|
. |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
1 |
|
2x 1 |
|||||||
0 |
|
|
|||||||
126

/2
29.sin x cos2 xdx.
|
|
0 |
|
|
|
|
1 |
|
|
dx |
|
32. |
|
|
|
||
|
|
|
|
. |
|
0 |
|
e x |
e x |
||
|
|
|
|
|
|
/4
35.tg3 xdx.
0
/2
30.cos x sin2 xdx.
0
1
dx
33.  .
.
0  x 2 1
x 2 1
|
3 |
dx |
|
|
|
||
36. |
|
|
. |
1 |
x x 2 |
||
|
|
|
|
|
1 |
dx |
|
|
31. |
|
. |
||
|
|
|||
|
0 |
e x |
1 |
|
|
|
|
|
|
/4
34.sin 4xdx.
0
Найти площади фигур, ограниченных линиями:
37. |
y |
4 x2, y |
0. |
|
|
38. |
y2 |
2 px, x |
h. |
|
|
||||||||||
39. |
y |
ln x, x |
|
|
e, y |
0. |
40. |
y |
x2, y |
2 |
x2. |
|
|
||||||||
41. |
y |
x2 , y = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
42. |
y |
cos2 x |
sin2 x, y |
0, x |
0, x |
/ 4. |
|
|
|
|
|||||||||||
43. |
y |
|
x |
|
1, |
|
y |
0, |
x |
2, |
x |
|
1. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||||||
44. |
y |
sin x, |
|
y |
|
x2 |
x. |
|
45. |
y |
arcsin2x, |
x |
0, y |
/ 2. |
|||||||
46. |
y |
sin 2x, y |
1, |
x |
/ 2, |
где |
/4 |
x |
|
/ 2. |
|
||||||||||
47. |
x2 |
|
y2 |
|
1, |
x |
2. |
|
|
|
|
|
|
|
|
|
|||||
48. |
xy |
4, |
x |
|
|
4, |
|
y |
4, |
x |
0, |
|
y |
0. |
|
|
|
|
|||
|
|
|
x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49. |
y |
|
|
y |
|
|
x. |
|
|
|
|
|
|
|
|
|
|
||||
50. |
y |
|
x 2 |
1, |
y |
|
0, x |
2, |
x |
2. |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||||||||
51. |
Найти площадь фигуры, заключенной между параболой |
||||||||||||||||||||
y |
x2 |
|
2x |
|
2, касательной к ней в точке (3, 5) |
и осью Оу. |
|||||||||||||||
127

52. |
Найти площадь фигуры, заключенной между параболой |
|||||||||||||||||||||||
y |
x2 |
4x 3 |
и |
касательными к |
ней в точках (0, 3) |
и |
||||||||||||||||||
(3, 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти длину дуги кривой: |
|
|
|
|
||||||||||||||||||
53. |
y |
|
|
x3 / 2 от x |
|
0 |
до x |
4. |
|
|
|
|
||||||||||||
54. |
y |
|
x2 |
1, |
|
отсеченной осью Ох. |
|
|
|
|||||||||||||||
55. |
y |
|
|
a |
e x / a |
|
e |
x / a |
от x |
0 |
до x |
a. |
|
|||||||||||
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
56. |
y |
|
ln cos x |
|
от |
|
x |
|
0 |
до x |
|
/ 6. |
|
|
||||||||||
57. |
y |
|
|
lnsin x |
от |
x |
|
|
/ 3 |
до x |
2 |
/ 3. |
|
|
||||||||||
58. |
y |
|
|
x2 |
|
|
1 |
ln x |
от |
|
x |
1 до |
x |
e . |
|
|
||||||||
4 |
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
59. |
y 2 |
|
|
|
|
4 |
(2 |
|
x)3 |
от |
x |
|
1 до |
x |
2 . |
|
|
|||||||
|
|
|
|
9 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
60. |
y |
|
|
|
|
x2 от х = 0 |
до |
x |
2 . |
|
|
|
|
|||||||||||
61. |
x |
et sint, |
y |
et cost, |
0 |
t |
|
/ 2. |
|
|
||||||||||||||
62. |
Астроиды |
|
x |
|
acos3 t, |
y |
asin3 t . |
|
|
|||||||||||||||
63. |
Кардиоиды |
|
|
|
a 1 |
cos |
, |
a |
0, |
0 |
2 . |
|
||||||||||||
|
Найти объемы тел, образованных вращением фигуры, |
|
||||||||||||||||||||||
ограниченной линиями: |
|
|
|
|
|
|
|
|||||||||||||||||
64. |
y2 |
|
|
2 px, x |
|
h вокруг оси Ox. |
|
|
|
|
||||||||||||||
65. |
y |
4 |
|
|
|
x2 , y = 0, |
|
x = 0, где x |
0 вокруг: 1) оси Ох; |
2) |
||||||||||||||
оси Оу . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x2 , |
|
|
|
|
|
вокруг оси Ох. |
|
|
|
|||||||||||
66. |
y |
|
|
y |
|
|
x |
|
|
|
||||||||||||||
67. |
y |
|
|
e x , |
|
x |
|
0, |
|
x |
1, |
y |
0 |
вокруг: 1) оси Ох; 2) оси Оу. |
|
|||||||||
128

68. |
y |
x2 |
1, |
y |
0, |
x 1, x |
2 вокруг: 1) оси Ox; 2) оси Оу. |
69. |
y |
x3, y |
1, x |
0 вокруг: 1) оси Ох; 2) оси Оу. |
|||
70. |
y |
x |
x2 , y |
0 |
вокруг |
каждой из следующих прямых: |
|
1) |
y = 0; |
2) x = 0; |
3) x = 2; |
4) x= |
2; |
5) y = 1; |
6) y = 2. |
|
|||||||||||
71. |
y = lnx, |
y = 0, |
x = e |
вокруг каждой из следующих |
|||||||||||||||
прямых: |
y = 0; |
2) x = 0; |
|
3) |
y = |
1; |
4) x = 1; |
|
5) x = |
1; |
|||||||||
6) y = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
72. |
y |
|
sin x , |
y = 0, |
0 |
x |
|
вокруг каждой из следующих |
|
||||||||||
прямых: |
y = 0; |
2) x = 0; |
|
3) |
x |
2 |
; |
4) x = |
1; |
5) x = |
2; |
||||||||
6) |
y = 1; |
7) |
y = |
2. |
|
|
|
|
|
|
|
|
|
|
|
||||
73 x2 |
|
y2 |
4, |
y = 2, |
y = 0 вокруг оси Ох. |
|
|
|
|||||||||||
74. |
y |
|
x, |
y |
|
x2 вокруг: 1) |
оси Ох; 2) |
оси Оу. |
|
|
|
||||||||
75. |
y |
|
cos2x , |
y 0, x = 0, |
где, |
0 |
x |
/ 4 вокруг: 1) оси Ох; |
|||||||||||
2) оси Оу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
76. |
y |
|
sin x , |
y |
|
0, |
где |
2 |
|
х |
3 |
вокруг |
каждой |
из |
|||||
следующих прямых: 1) y = 0; |
2) x = 0; |
3) х |
; |
4) y = |
2. |
||||||||||||||
77. |
y |
|
2x x2 , |
|
y |
0 |
вокруг каждой из следующих прямых: |
||||||||||||
1) x = 0; |
2) |
y |
|
0; |
|
3) x = |
1; |
4) y = 1. |
|
|
|
|
|||||||
78. |
y |
|
4/x, |
x = 1, |
x = 4, |
y |
0 |
вокруг: 1) оси Ох; 2) |
оси Оу. |
||||||||||
79. |
y |
1 |
, x |
1, |
x |
1, |
y |
0 |
вокруг: 1) оси Ох; 2) оси Оу. |
||||||||||
|
|
|
|||||||||||||||||
1 |
x2 |
||||||||||||||||||
80. |
y |
|
x2 |
1, |
y |
3x 1 вокруг оси |
Оу. |
|
|
|
|||||||||
|
Найти площадь поверхности, образованной вращением |
||||||||||||||||||
вокруг оси Ох: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
81. |
Дуги синусоиды y |
sin x от |
x |
0 до x . |
|
|
|
||||||||||||
129
