Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 800583

.pdf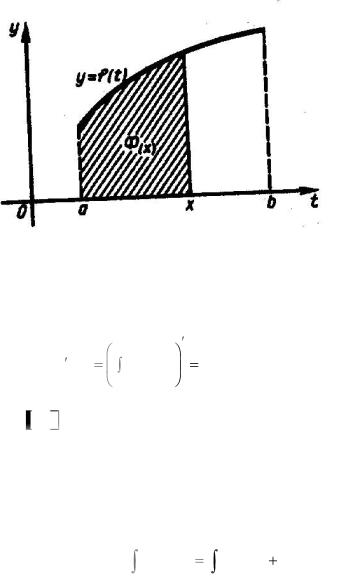

Скачиваний:

Добавлен:

01.05.2022

Размер:

6.43 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2411 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Рис. 25

Теорема. Производная интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему

	x
пределу, т.е. Ф x	f	t dt	f x .
	a
Таким образом, установлено, что любая непрерывная на
отрезке a, b функция		f (x) имеет на		этом отрезке
первообразную, причем		функция	Ф(x)	– интеграл с

переменным верхним пределом – является первообразной для

f (x) . А так как всякая другая первообразная для					функции
f (x) может отличаться от Ф(x)			только на постоянную, то
установлена	связь между	неопределенным		и определенным
			x
интегралами	в виде	f x dx	f t dt	C,	где С –

произвольная постоянная.

100

3.6. Формула Ньютона-Лейбница

Вычисление определенных интегралов методом, основанным на определении интеграла как предела интегральной суммы, как правило, связано с большими трудностями. Существует более удобный метод вычисления определенных интегралов, который, как будет показано,

основан	на	установленной	ранее связи	между
неопределенным и		определенным интегралами.		Было
установлено,	что функция f (x) -		непрерывная на отрезке

a, b , имеет на этом отрезке первообразные, причем одной из

них является функция Ф(x) f (t)dt.

Пусть F(x) – любая другая первообразная для функции

f (x) на том же отрезке

a, b .

Так как первообразные Ф(x) и

F(x) отличаются

на

постоянную,

то

имеет место

равенство

f (t) dt

F (x)

где

–

некоторое

число.

Подставляя в

это

равенство

значение

a ,

имеем

f (t) dt

F (a)

F(a)

F(a), т. е.

для

любого x

a, b

f (t) dt

F (x)

F (a).

Полагая

b ,

получаем

основную

формулу

интегрального исчисления

f (x) dx

F (b)

F (a),

(3.6)

101

которая называется формулой Ньютона-Лейбница. Разность F(b) F(a) принято условно записывать: F (x) ba , и поэтому

формула (3.6) принимает вид

f (x) dx F (x) ba .

Подчеркнем, что в формуле (3.6) в качестве F(x) можно

взять любую первообразную для f (x)	на отрезке	a, b .
Формула (3.6) дает простой	метод	вычисления

определенного интеграла: определенный интеграл от непрерывной функции равен разности значений любой ее первообразной, вычисленных для верхнего и нижнего пределов интегрирования. Эта формула открывает широкие возможности для вычисления определенных интегралов, поскольку задача вычисления определенного интеграла сводится к задаче вычисления неопределенного интеграла,

которая достаточно полно изучена.											Рассмотрим			п р и м е р ы.
			b					b
	1.
	1.		sin x dx				cos x		cosa cosb.
			a					a
								a

			2							2
	2.		(3x2		1) dx (x3				x)	2	(23	2)	(03	0) 6.
	2.		(3x2		1) dx (x3				x)	0	(23	2)	(03	0) 6.
			0							0
			0
	3.		2 dx	ln x		12	ln 2		ln1		ln 2.
			2 dx

			1 x
	4.		1 x
	4.
1	dx				1
			arctg x				arctg1		arctg(		1)					.

11 x		2			1							4	4		2
11 x

102

3		dx			3

				1 x2
5.			ln x		ln(3	10).


	1 x2
0					0
0					0

З а м е ч а н и е. Формула Ньютона-Лейбница была выведена в предположении, что подынтегральная функция f (x) непрерывна. При некоторых условиях формула НьютонаЛейбница имеет место и для разрывных функций.

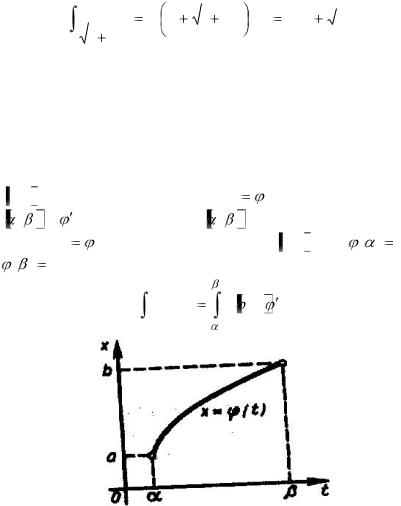
3.7. Замена переменной в определенном интеграле Теорема. Пусть f (x) – непрерывная функция на отрезке

a, b .	Тогда, если: 1) функция x			(t) дифференцируема на
,	и	(t) непрерывна на	,	; 2)	множеством значений
функции x		(t) является	отрезок		a, b ; 3)	( ) a и
( )	b	(рис. 26), то справедлива формула
		b
		f (x)dx	f	(t)	(t)dt.	(3.7)

Рис. 26

Формула (3.7) называется формулой замены переменной или подстановки в определенном интеграле.

З а м е ч а н и е 1. Если при вычислении неопределенного интеграла с помощью замены переменной

103

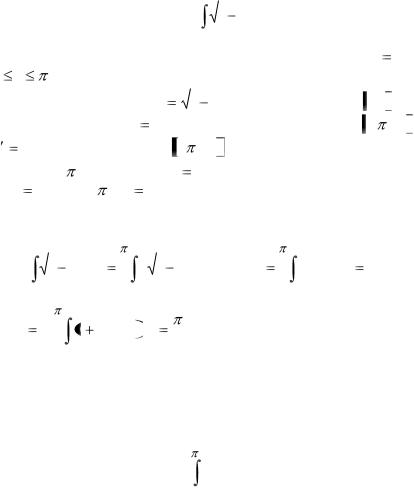
от новой переменной t следует возвращаться к старой переменной x , то при вычислении определенного интеграла этого делать не нужно, так как теперь следует найти число, которое согласно доказанной формуле равно значению каждого из рассматриваемых интегралов.

x2 dx.

Пример 1.

Вычислить

Решение.

Рассмотрим

подстановку

sint ,

/ 2.

Проверим

законность такой подстановки.

Во-

первых,

функция f (x)

x2 непрерывна на

0, 1 ;

во-

вторых,

функция

sint

дифференцируема на

0, / 2 и

cost

непрерывна на

/ 2

и, в третьих, при изменении

от 0 до

/ 2 функция

x sint

изменяется от 0 до 1, причем

x(0)

х( / 2)

Таким образом, данная подстановка

удовлетворяет всем условиям теоремы. Применяя формулу (3.7), получаем

1			/ 2				/ 2
1		x2 dx		1 sin2 t cost dt			cos2 t dt
0		0					0
1	/ 2
1		1 cos2t dt				.

2	0				4

З а м е ч а н и е 2. При использовании формулы (3.7) необходимо проверять выполнение перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен и неверный результат.

Пример 2. Вычислить dx.

104

Решение.

Имеем

dx x

С другой стороны,

0 sin2 x

cos2 x

0 cos2 x (1

tg2 x)

Подстановка

tg x

формально приводит к следующему

результату:

d (tg x)

tg2 x

t 2

Получен

неверный

результат,

так

как

0 .

Это

произошло потому, что

функция

tg x

разрывна

при

x 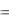/ 2 и не удовлетворяет условиям теоремы.

3.8. Формула интегрирования по частям в определенном интеграле

Теорема. Если функции

u(x) и

v(x) имеют

непрерывные производные на отрезке a, b , то справедлива формула

b	b	b
u dv uv		v du.	(3.8)

a	a	a

Формула (3.8) называется формулой интегрирования по частям в определенном интеграле.

Пример 1. Вычислить ln xdx.

105

Решение.

Положим

ln x ,

dv dx ;

по

формуле

(3.8)

ln xdx

x ln x

(x ln x

Пример 2.

Вычислить

x ex

dx.

Решение.

Положим

ex dx;

dx,

по

формуле

(3.8)

x e

dx xe

dx e

(x 1)

Пример 3. Вычислить

arctg x dx.

Решение.

Положим

arctg x ,

dx ;

x и по формуле (3.8) находим

1 xdx

arctg x dx

(x arctg x)

x arctg x

ln(1

0 1

отсюда

находим

отсюда

имеем

отсюда

x2 )

3.9. Некоторые физические и геометрические приложения определенного интеграла

1. Площадь криволинейной трапеции. Пусть на плоскости Oxy дана фигура, ограниченная отрезком a, b оси Ох, прямыми x a , x b и графиком непрерывной и неотрицательной функции y 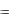f (x) на a, b . Это

106

криволинейная трапеция, площадь s которой может быть вычислена по формуле

	b
s	f (x) dx.	(3.9)

Итак, определенный интеграл от неотрицательной

непрерывной функции	f (x) по	a, b		численно равен
площади криволинейной	трапеции	с	основанием		a, b ,
ограниченной сверху графиком функции			y	f (x) . В	этом и

заключается геометрический смысл определенного интеграла.

Пример 1. Найти площадь фигуры, ограниченной

графиком функции y

прямой x

1 и осью Ох.

Решение.

По

формуле

(3.9)

имеем

0 x dx

Если

1, то s

1/2;

если

2, то s

1/3, и т. д.

Пусть фигура ограничена снизу и сверху графиками

функций

f1(x)

f2 (x), f1(x)

f2 (x), a

x b

(рис. 27),

где

f1 (x),

f2 (x)

две непрерывные функции. Если

обе функции неотрицательны, то площадь s данной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху соответственно графиками функций

y 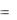f2 (x), y 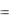f1(x).

Следовательно,

b		b	b
s	f2 (x)dx	f1(x)dx	f 2 (x) f1(x) dx.	(3.10)
a		a	a

Заметим, что формула (3.10) справедлива и тогда, когда f1(x) и f2 x не являются неотрицательными.

107

графиками функций y			f (x) x		и y	f	2		(x)	2	x2 (рис. 28).
			1				2
	Решение. Найдем		абсциссы		точек			пересечения прямой
y	x	с параболой y	2	x2 .	Решая				систему		уравнений
y	x,	получаем	x1	2,	x2	1.		Это		и есть пределы
		получаем	x1	2,	x2	1.		Это		и есть пределы
y	2	x2 ,

интегрирования. Искомая площадь фигуры согласно формуле

(3.10)	такова:
1					1		x	3		x	2	1	9
1					1
s	f		(x)	f (x) dx	(2 x2 ) x dx	2x								.

		2
		2		1			3		2			2	2
2					2		3		2			2	2
2					2

З а м е ч а н и е. Для вычисления площади криволинейной трапеции в случае, когда верхняя граница задана

параметрически	уравнениями	x	(t), y	(t),	t	,
причем ( ) a ,	( ) b , в	формуле (3.9)		надо	сделать
	108

замену переменной, положив x		(t), dx	(t)dt . Тогда
получим
s	(t)	(t)dt .

Рис. 29		Рис. 30
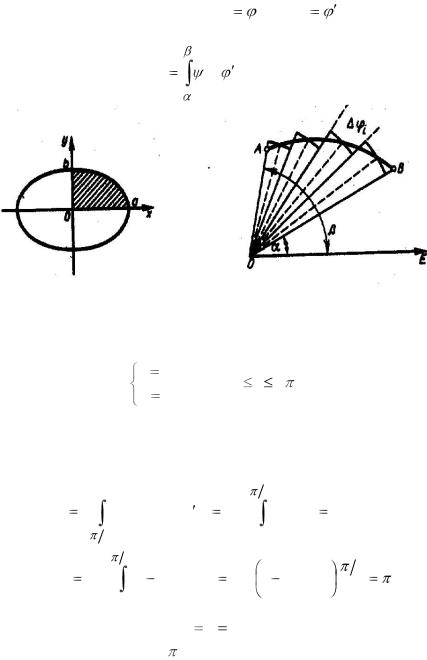
Пример 3. Вычислить площадь фигуры, ограниченной
эллипсом
x	a cos t,	0 t 2 .
y	b sin t,	0 t 2 .
y	b sin t,

Решение. Эллипс симметричен относительно осей координат, поэтому достаточно вычислить площадь части фигуры, находящейся в I четверти (рис. 29). Следовательно, искомая площадь равна

0				2
s 4 b sin t(a cost) dt			4ab	sin2 tdt
2				0
2					1			2
2
2ab	(1 cos2t)dt		2ab t			sin 2t			ab.

					2		0
0					2		0
0		a b	R ,
В частности,	если	a b	R ,	то	получаем			известную
формулу площади круга		R2.

109

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2411 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20226.2 Mб1Учебное пособие 800579.pdf
#
01.05.2022398.1 Кб1Учебное пособие 80058.pdf
#
01.05.20226.29 Mб7Учебное пособие 800580.pdf
#
01.05.20226.35 Mб3Учебное пособие 800581.pdf
#
01.05.20226.43 Mб4Учебное пособие 800582.pdf
#
01.05.20226.43 Mб1Учебное пособие 800583.pdf
#
01.05.20226.45 Mб4Учебное пособие 800584.pdf
#
01.05.20226.45 Mб3Учебное пособие 800585.pdf
#
01.05.20226.49 Mб4Учебное пособие 800586.pdf
#
01.05.20226.52 Mб12Учебное пособие 800587.pdf
#
01.05.20226.61 Mб4Учебное пособие 800588.pdf