
Практика решения задач по физике. Часть 5. Квантовая физика. Евсюков В.А., Показаньева С.А
.pdf
Отсюда получаем sin |
|
|
mc(p p ) |
. Для p=1,02 МэВ/с, |
p’=0,255 |
||||
|
|
||||||||
|
|
2 |
|
2pp |
|
||||
МэВ/с, где |
с=3108 м/с, |
угол отклонения рассеянного фотона |
|||||||
|
|
|
|
|
|
||||
2arcsin |
0,91 10 30 (3 10 8 )2 (1,02 0,255 ) |
|
2 arcsin 0,276 |
32 0 |
|||||
|
|||||||||
|
|
2 1,02 0,255 1,6 10 13 |
|
||||||
5.33. При описании взаимодействия фотона со свободным неподвижным электроном будем исходить из законов сохранения
энергии тс2 |
E |
(1) |
и |
импульса |
k |
p k (2). |
При |
|||||||||||||
этом |
учтем |
|
релятивистские |
соотношения: |
E T mc2 |
(3), |
||||||||||||||
p |
|
/c (4). Выражения (3) и (4) для Е и р позволяют |
||||||||||||||||||
T(T 2mc2 ) |
||||||||||||||||||||
равенства (1) |
и (2) переписать в виде |
|
T ; |
(5) |
||||||||||||||||
|
|
|
2 |
|
2 |
p |
2 |
|
|
2 |
(k |
2 |
k |
2 |
2kk |
|
cos ) |
|
||
|
|
|
|
(k k ) |
|
|
|
|
|
|
||||||||||
T(T 2mc2 )/c2 |
2 ( 2 |
2 2 cos ) T(T 2mc2 ) |
(6) |
|||||||||||||||||
Подставляем (5) в (6): 2 2 |
( T)2 |
2 ( T)cos T(T 2mc2 ), |
||||||||||||||||||
2 2 |
2 2 2 T T 2 |
2 2 2 |
cos 2 T cos T 2 2mc2T |
|||||||||||||||||
( 2 2 T)(1 cos ) mc2T 2( 2 T)sin2 ( /2) mc2T ,
где - искомая величина. Получили квадратное уравнение
для : 2 T |
mc2T |
, sin |
|
0. Одним из корней этого |
|
||||||
|
|
||||||||||
2sin2 |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
уравнения, имеющего физический смысл, является величина |
|
||||||||||
|
|
T |
|
|
|
|
|
|
|
||
|
|
(1 |
|
1 2mc2 /(T sin |
|
)) |
(7) |
||||
|
|
|
|
||||||||
|
|
|
2 |
|
2 |
|
|
|
|||
21

Итак, энергия первичного фотона равна
(T /2) {1 
 1 2mc2 /(T sin2 /2)}. Для Т=0,45 МэВ и =1200
1 2mc2 /(T sin2 /2)}. Для Т=0,45 МэВ и =1200
2mc2 |
|
2 0.511 |
3, энергия кванта =3Т/2=0,68 МэВ. |
|||
|
|
|
||||
T sin2 |
|
|
0.45 |
3 |
|
|
|
|
|
||||
24
5.34.Из закона сохранения энергии для системы фотон – свободный неподвижный электрон следует: T , где Т – кинетическая энергия электрона после взаимодействия с
фотоном. При const и T Tmax Tm : Tm min , или
Tm 2 c . Из формулы c (1 cos ) видно, что max
max
при |
, |
т.е. |
|
|
|
|
2 c . |
|
|
|
|
|
|
|
|||||||||
|
|
max |
|
|
|
|
|
|
|
||||||||||||||
|
|
Для Т=Тm и |
по формуле (7) задачи 5.33. получим: |
||||||||||||||||||||
|
Tm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(1 1 |
2mc2 |
) |
|
. |
Отсюда |
длина волны |
|
рентгеновского |
||||||||||||||
|
|
Tm |
|
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
излучения |
|
|
|
|
|
|
|
. |
Для |
||||||||||||||
|
2 c/ 4 c/[T |
(1 1 2mc2 /T )] |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
m |
|
|
|
Тm=0,19МэВ: mc2 /T |
|
0,511/0.19 2,70 ; |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
T (1 |
|
|
|
|
) 0,67МэВ; |
|
|
|
|
|
|
|
|
||||||||||
1 2mc2 |
/T |
|
|
|
|
|
|
|
|
||||||||||||||
m |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
длина волны |
4 0,66 10 15 3 108 |
3,7 10 12 |
м 3,7пм. |
|
|
||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,67 106 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.35. |
|
Из |
|
параллелограмма |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
импульсов |
имеем: |
psin k sin |
(1), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
pcos (k k cos ) |
(2). При делении (1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
на |
(2) |
и |
заменах |
k /c, k /c |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
получим: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
/ cos |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
По условию , т.е. / 1 / . |
|
|
|
(4) |
|||||||||||||||||||||||||||||
Из |
формулы |
комптоновского |
смещения |
|
|
|
c (1 cos ) |
|||||||||||||||||||||||||||||
определяем: |
|
|
|
|
|
|
|
|
cos 1 / c |
, |
|
|
|
|
|
(5) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
(6) |
||||||||||
|
|
|
|
sin |
1 (1 / )2 |
|
2 / |
c |
( / )2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|||||
Подставляем |
|
|
(4) |
|
– |
(6) |
в |
|
(3) |
|
|
|
и |
получаем: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 / |
c |
( / |
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
tg |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 / 1 / c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
c 2 / c |
( / c )2 |
|
|
|
2 c ( )2 |
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 c / 1 |
(7) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( c / 1) |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
( c ) |
|
|
|
|
|
|
|
|
|
|
|
c / 1 |
|
|
||||||||||||||||||
|
|
|
Теперь учтем, что с |
2 /mc и 2 c/ и перепишем |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
(7) в виде |
|
|
|
|
tg |
|
|
4 /(mc ) 1 |
|
|
|
|
|
|
(8) |
|||||||||||||||||||||
|
|
|
|
|
|
|
1 /mc2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Для 0,15МэВ и 3,0пм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
tg |
|
|
4 1,05 10 34 |
/(0,91 10 30 3 108 |
3,0 10 12 ) 1 |
0,6, угол 310 . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 0,15/0,511 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
5.36. Радиус кривизны траектории электрона отдачи в |
|||||||||||||||||||||||||||||||||
магнитном поле |
найдем |
|
из |
динамического |
уравнения |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 2 |
|
|
|
|
|
|
|
|
|
m /eB , где |
m |
|
|
|
m/ |
1 2 /c2 |
- |
|||||||||||||||||||
|
/ eB , B : |
r |
|
|||||||||||||||||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
релятивистская масса электрона. Таким образом, нам предстоит
23

вычислить |
|
скорость |
|
электрона |
и |
|
релятивистскую |
поправку |
||||||||||||||||||
|
|
|
|
. При этом будем исходить из законов сохранения: |
||||||||||||||||||||||
1. 1 2 |
|
|||||||||||||||||||||||||
1) |
|
энергии T , |
где |
|
Т – кинетическая энергия |
|||||||||||||||||||||
электрона отдачи; отсюда T ; |
|
|
|
|
|
|
|
|||||||||||||||||||
2) |
|
|
|
импульса |
|
при |
|
(лобовом |
столкновении) |
|||||||||||||||||
k p k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
p (1/c)( ) cp T cp |
|||||||||||||||||||||||||
2 T . |
|
По условию /mc2 |
, |
т.е. mc2 . |
Учитывая |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
соотношения |
|
p m / |
1 2 |
и |
|
T mc2 / |
1 2 mc2 , |
|||||||||||||||||||
получим равенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
cm |
|
|
2 |
|
|
|
mc 2 |
|
2 |
|
|
|
|
|
v2 . |
||||||||
|
|
|
|
2 mc |
|
|
|
|
|
|
mc |
|
c c(1 2 ) 1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
||||||||||||
|
|
1 2 |
|
1 2 |
|
|||||||||||||||||||||
Возводим в квадрат, сокращаем на общий множитель, находим:
( c)2 (1 2 )2 (c2 2 ) c (1 2 )2 (c )
c (1 |
2 )2 |
1 |
. |
|
|
|
|
|
Далее: |
|
|
|
|
|
|
|
|
|
|
|
[(1 |
2 ) 2 |
1] |
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
1 |
2 |
|
1 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(1 |
2 )2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[(1 |
2 ) 2 |
1] |
2 |
|||||||||||||||||||||||||||
|
2(1 2 ) |
|
|
, |
|
|
1 |
|
|
|
|
|
|
|
|
(1 2 )2 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(1 |
2 )2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 2 |
|
2(1 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Теперь можем определить радиус кривизны траектории |
||||||||||||||||||||||||||||||||||||||||||||||||
электрона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
m |
|
|
c[(1 2 )2 |
|
1] |
|
(1 2 )2 |
1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eB |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eB |
|
|
|
|
1 2 |
|
|
|
|
|
|
(1 |
2 )2 |
1 |
|
|
2(1 |
2 ) |
|
|
|
|
||||||||||||||
|
mc |
|
(1 2 ) 2 1 |
|
2mc |
|
(1 ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2eB |
|
|
1 2 |
|
|
|
|
|
|
|
eB |
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Итак, |
|
2mc |
|
|
(1 ) |
. Для В=0,12 |
Тл и 2 |
радиус |
||||||||||||||||||||||||||||||||||||||||
|
|
eB |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
кривизны |
|
|
2 0,91 10 30 |
|
3 10 8 |
|
6 |
3,4 10 2 м 3,4см . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
1,6 10 19 0,12 |
|
|
|
5 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.37. Здесь достаточно воспользоваться принципом обратимости механических явлений, в частности, для столкновения двух частиц, и комптоновское смещение длины волны определить величиной с (1 cos ) .
2.РАССЕЯНИЕ ЧАСТИЦ. АТОМ РЕЗЕРФОРДА-БОРА
5.38.Согласно представлениям Томсона невозбужденный атом водорода представляет собой равномерно заполненный положительным зарядом шарик, в центре которого находится электрон. Суммарный положительный заряд шарика равен абсолютному значению заряда электрона е. В возбужденном состоянии электрон атома водорода совершает колебания относительно центраатома.
Допустим, что радиус атома водорода, т.е. воображаемого шарика, равен R. Напряженность поля на расстоянии r от центра
равномерно заряженного шарика E (ke/ R3 )r , где k 1/4 0
(см. приложения теоремы Гаусса). При этом сила, действующая
на смещенный электрон, равна F ( e)E (ke2 / R3 )r . |
Отсюда |
коэффициент квазиупругости системы x ke2 / R3 |
. В |
возбужденном атоме водорода электрон в течение некоторого промежутка времени будет совершать колебания частотой
|
x/m (e/ R) k /mR , испуская свет с длинной волны |
|
||
|
2 c/ (2 c/e) |
|
|
|
|
mR3 /k. |
(1) |
||
|
Энергия ионизации атома |
водорода равна |
работе |
|
отщепления электрона от атома. Если потенциал поля в центре атома в модельном представлении Томсона обозначить через 0 ,
то работа по вырыванию электрона A e 0 и, следовательно,
25
энергия ионизации E e 0 . Потенциал 0 найдем из условия
0 |
R |
ke |
rdr |
ke |
|
3ke |
. Принимая 0 , |
получаем |
|||
|
|
|
|
||||||||
|
0 |
R3 |
R r2 |
|
2R |
|
|
|
|||
0 |
3ke/2R,E 3ke2 /2R. Отсюда радиус атома водорода |
||||||||||
|
|
|
|
|
R 3ke2 /2E 3e2 /(8 0E). |
(2) |
|||||
Для Е=13,6 эВ радиус R |
|
3 1,6 10 19 |
1,6 10 10 м 0,16нм . |
||||||||
8 8,85 10 12 13,6 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
Подставляя выражение (2) в (1), получим длину волны
испускаемого света |
|
3ce2 |
|
|
3m |
|
. Вычисление дает 0,24мкм . |
||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
4 0E 2E |
|
|
|
|
|
||||||
|
|
|
5.39. |
|
Воспользуемся |
формулой |
(5.1а) |
сборника |
|||||||||||
tg |
|
k |
q1q2 |
|
, |
из |
которой |
прицельный |
параметр |
||||||||||
|
2bK |
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b кq1q2 /(2Ktg /2) . Заряды q1 |
2e (альфа-частицы) и q2 79e |
||||||||||||||||||
(ядра |
атома |
золота). |
Для |
к=0,27 |
МэВ |
и 600 |
прицельный |
||||||||||||
параметр b |
79ke2 |
|
|
79 9 109 |
1,6 10 19 |
0,73 10 12 |
м 0,73пм. |
||||||||||||
Ktg /2 |
|
0,27 106tg300 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
5.40. а) Лобовое соударение -частицы |
(q1 2e) с |
|||||||||||||||
тяжелым покоящимся ядром атома свинца (q2 |
82e). |
|
|||||||||||||||||
Вточке наибольшего их сближения кинетическая энергия
-частицы полностью переходит в потенциальную энергию
электрического взаимодействия, |
т.е. K kq1q2 /rmin . Отсюда |
||||||||
r |
kq q |
2 |
/ K 164ke2 /K . Для |
К=0,40 |
МэВ минимальное |
||||
min |
1 |
|
|
|
|
|
|
||
расстояние сближения r |
|
164 9 109 1,6 10 19 |
|
0,59 10 12 м 0,59пм. |
|||||
0,4 106 |
|||||||||
|
|
|
min |
|
|
||||
б) Лобовое соударение -частицы с легким ядром атома
7 Li (q3=3e). В этом случае кинетическая энергия -частицы не
26

полностью перейдет в потенциальную энергию при наибольшем сближении частиц, поскольку система частиц в целом будет совершать движение.
При заданной кинетической энергии -частицы релятивистской поправкой практически можно пренебречь, поэтому воспользуемся некоторыми формулами классической механики. На большом расстоянии между -частицей и ядром атома 7Li результирующий импульс системы p p 
 2m K
2m K
(ядро атома 7Li покоилось). В момент максимального сближения частиц ( r rmin ) в К/-системе отсчета, связанной с ядром 7Li
-частица останавливается, тогда как для неподвижного наблюдается система частиц как целое движется со скоростью центра масс с . Скорость с в рассматриваемый момент времени
найдем |
из |
|
закона |
|
сохранения |
импульса: |
|
p |
(m mLi ) c , |
||||||||||||||||||||||||
c |
|
|
|
/(m mLi ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2m K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Далее |
|
|
воспользуемся |
|
законом |
сохранения |
энергии: |
|||||||||||||||||||||||
|
kz |
z |
e2 |
|
|
|
(m m |
Li |
) 2 |
|
|
|
|
|
|
|
|
|
4 |
He ) |
|
|
|
|
|
|
|
|
|||||
K |
1 |
2 |
|
|
|
|
|
c |
, |
где |
|
z1 2 (для 2 |
и z2 |
z |
|
(для |
|||||||||||||||||
rmin |
|
|
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
произвольного ядра |
ZA X , |
в частности для лития z=3). Отсюда |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2kZe2 |
|
m K |
|
|
|
m |
|
|
|
|
|
2kZe2 |
|
|
2kZe2 |
|
m |
|||||||
получаем: |
K |
|
|
|
|
|
|
|
|
Li |
|
|
K |
|
|
|
r |
|
|
|
|
(1 |
|
) . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
r |
|
m m |
|
|
|
|
|
|
r |
|
min |
|
K |
|
|
|
m |
||||||||||
|
|
|
|
|
|
|
|
|
|
m m |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
min |
|
|
Li |
|
|
|
Li |
|
min |
|
|
|
|
|
|
|
|
Li |
||||||
Для К=0,40 МэВ минимальное расстояние |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
r |
|
|
2 9 109 |
3 1,6 10 19 |
|
(1 |
|
4 |
) 3,4 10 14 м 0,034пм . |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
min |
|
|
|
|
0,40 106 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
5.41. Описание процесса рассеяния -частиц |
на |
ядрах |
||||||||||||||||||||||||||||
ZA X |
атомов |
|
некоторого элемента |
|
представляет |
собой |
решение |
||||||||||||||||||||||||||
задачи о движении частицы в центральном поле сил. Однако мы
27
не предполагаем получить свое решение этой задачи, поскольку оно давным-давно получено, а воспользуемся некоторыми фрагментами общего решения.
Характеристики движения частицы в центральном поле сил определяются начальными условиями и законом действующей силы. При этом имеет место сохранение механической энергии и момента импульса частицы.
Прицельное расстояние -частицы относительно силового центра (атомного ядра ZA X ) согласно данным задачи
b |
kq q |
|
kZe2 |
, |
где |
Е |
– |
энергия |
частицы, |
равная |
||||||||
|
1 |
|
2 |
|
|
|||||||||||||
|
2Etg /2 |
Etg /2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
кинетической энергии К, заданной на большом расстоянии от |
||||||||||||||||||
рассеивающего центра. Кулоновская сила, действующая на - |
||||||||||||||||||
частицу, |
|
|
, |
или |
F /r2 , |
где 2kZe2 |
0 . |
Момент |
||||||||||
F r |
||||||||||||||||||
|
|
|
|
|
r3 |
|
|
|
|
|
|
[r,m v] , где |
|
|
||||
импульса относительно |
центра сил |
L Lz |
m |
- |
||||||||||||||
масса |
|
|
-частицы. |
Поскольку |
L const |
|
, |
то |
модуль |
|||||||||
L bm v0 b 2m E . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
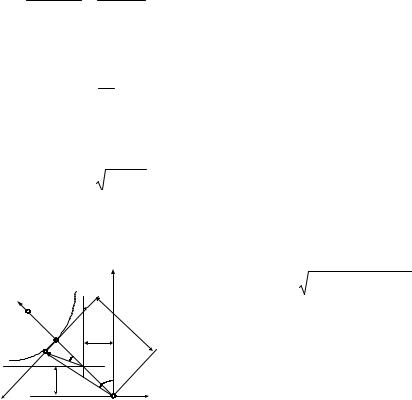
Траектория -частицы представляет собой ветвь |
||||||||||||||||
гиперболы, |
полярное уравнение |
которой |
при >0 имеет |
вид |
||||||||||||||
|
|
|
|
|
|
|
|
r p/( cos 1) , |
где |
p L2 |
/m |
- |
||||||
|
|
|
|
|
y |
|
|
параметр, |
|
|
1 2EL2 /m 2 |
|
- |
|||||
|
F |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
А |
rmin |
эксцентриситет кривой. |
|
|
|
|
|
|
|||||||
|
|
А |
|
|
|
|
|
|
|
|||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||
|
В |
|
|
|
|
Примерный |
вид |
траектории |
- |
|||||||||
|
|
|
|
|
|
|||||||||||||
|
O' |
|
|
|
||||||||||||||
|
|
|
|
|
частицы показан на рисунке. Расстояние |
|||||||||||||
|
|
b |
|
r |
|
|
|
|||||||||||
|
|
|
|
x |
между силовым центром О и ближайшей |
|||||||||||||
|
|
|
|
O |
|
|||||||||||||
|
|
|
|
|
точкой |
А |
орбиты |
|
частицы |
равно |
||||||||
rmin |
p/( 1). Вычислим значения параметров орбиты: |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
p L2 |
/m |
|
b2 E |
|
kZe2 |
|
ctg2 /2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
kZe2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 2EL2 /m 2 |
1 Ctg2 /2 1/sin /2 csc / 2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Минимальное расстояние, на которое α -частица может |
|||||||||||||||||||||||||||||||||||||||
приблизиться |
|
к |
ядру, |
|
|
равно |
|
rmin |
|
|
p |
|
kZe2 |
ctg |
2 |
1 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
E |
2 |
|
/(sin /2 1) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
kZe |
2 |
|
|
|
cos |
2 / 2 |
|
|
sin |
/ 2 |
|
|
kZe |
2 |
|
|
|
|
1 sin |
2 / 2 |
|
|
|
|
|
||||||||||||||||||||
|
E |
|
|
|
|
sin |
2 / 2 |
|
|
sin / 2 |
|
|
|
|
sin( |
/ 2)(1 sin |
/ 2) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
E |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
kZe2 |
|
|
1 sin /2 |
|
|
kZe2 |
|
(1 csc /2), т.е. |
|
rmin |
|
|
kZe2 |
(1 csc |
|
). |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
E |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
sin /2 |
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
В случае ядра |
80200 Hg , Е=0,50 МэВ и =900 наименьшее |
||||||||||||||||||||||||||||||||||||||
расстояние r |
|
|
9 109 |
80 1,6 10 19 |
|
(1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
2) 0,56 10 12 м 0,56пм. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
0,50 106 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Радиус кривизны A в точке А траектории определим по формуле A v2A /an . Нормальное ускорение -частицы в точке А
a |
|
|
|
|
F |
|
2kZe2 |
потому, |
как в этой точке |
a |
=0. Скорость v |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
n |
|
|
|
|
|
m r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
найдем из закона сохранения энергии: E |
mvA2 |
|
|
2kZe2 |
. Отсюда |
|||||||||||||||||||||||||||||||||
2 |
|
rmin |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получаем |
2 |
|
2E 1 sin /2 , |
|
а затем |
радиус |
кривизны: |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
vA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
m |
1 sin /2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
A |
|
|
|
E |
|
|
1 sin /2 |
r2 |
|
|
|
|
E |
|
|
1 sin2 /2 |
( |
kZe2 |
)2 |
(1 sin /2)2 |
|
||||||||||||||||
|
kZe2 |
|
|
|
|
kZe2 |
|
|
sin /2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
1 sin /2 |
min |
|
1 sin2 /2 |
E |
|
|
|
|
|
||||||||||||||||||||||||
|
kZe2 |
|
1 sin /2 |
|
|
kZe2 |
ctg2 |
|
|
|
. Для числовых значений исходных |
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
E |
|
|
|
|
sin /2 |
|
|
E |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
величин A =0,23 пм.
5.42. Будем исходить из законов сохранения энергии и импульса системы протон - ядро, когда частицы до и после столкновения находятся на большом расстоянии друг от друга.
29
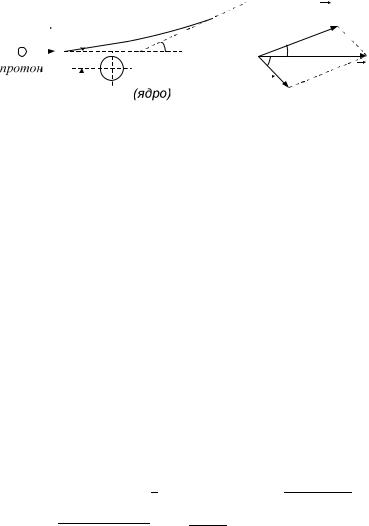
Пусть при этом - импульс протона до соударения, а |
и |
- |
|||
импульсы протона |
и ядра после их столкновения. Поскольку |
ядро |
|||
было |
неподвижным, можем написать: |
= |
|
, |
|
= |
+ |
(см. рис.). Тогда согласно |
закону |
||
|
|
||||
сохранения импульса
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
p |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
Ze |
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
протона.= 2 |
|
|
, где mp – масса, |
а К – кинетическая энергия |
|||||||||||||||||||||||||||||||
На основании закона сохранения энергии будем иметь: |
|
||||||||||||||||||||||||||||||||||
= |
+ |
|
|
|
|
|
= |
+ |
|
|
|
|
|
|
|
|
= . |
|
|
|
|
|
(1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
где |
|
|
|
|
|
|
|
Итак, |
имеем |
|||||
|
|
|
|
|
|
я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= + |
, |
|
|
|
|||||||
систему четырех уравнений: |
|
|
|
|
|
|
|
|
|
|
(4) |
||||||||||||||||||||||||
= |
+ |
|
|
|
|
|
, |
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|||||||||||||||
частицы,=b1/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
, |
|
|
(3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
кинетическая энергия налетающей |
||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
(СИ), К - |
|
|
= |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
– прицельное расстояние. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Из (1) и (2) легко получается соотношение: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
( |
|
) +( − |
|
|
|
|
) = => + − = 2 |
|
|
. |
(5) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя в (5) выражение для |
|
, взятое из (3), получим: |
|
||||||||||||||||||||||||||||||||
Теперь примем условие2 |
− |
1 |
|
|
т.е.= (1 + |
2 . |
|
|
|
|
|
|
(6) |
||||||||||||||||||||||
|
, |
,) 2 |
|
|
. |
|
Тогда |
соотно- |
|||||||||||||||||||||||||||
шение (6) примет вид |
|
|
|
|
я |
|
|
|
, т.≈е. |
|
≈ 0 |
|
|
|
|
|
(7) |
||||||||||||||||||
|
|
|
|
|
|
|
( |
/ ) |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
|
2 |
|
|
|
< => 2 = 2 |
|
|
|
|
=> |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( / ) |
|||||||||||||
Из (7) получаем: |
|
|
|
2 |
(1− |
|
, |
|
|
|
) ≈ |
|
|
|
4 |
|
|
|
|
|
|
≈ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
=> = 2 / |
1+ 2( /2) |
= 2302 |
|
/ |
1+ (2 / 2 )2 |
. |
|
||||||||||||||||||||||||||||
