Практика решения задач по физике. Часть 5. Квантовая физика. Евсюков В.А., Показаньева С.А

относительно подвижного ядра будет иметь меньшую энергию, < E. При этом относительное изменение энергии кванта

( ) 1 .

По законам сохранения импульса и энергии можем

, где Т – кинетическая энергия ядра. Перепишем последнее равенство через импульс:

где m – масса ядра. Отсюда получаем:

2 2mc2 2mc2 0 mc2 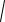(mc2)2 2mc2

mc2( 1 2 1). mc2

Выражение в скобках разложим до слагаемого второго порядка

5.272. Источник и поглотитель γ – излучения состоят из свободных ядер 191 r . Ядра источника находятся в возбужденном состоянии, ядра поглотителя – в основном состоянии. Пусть энергия возбуждения ядра 191 r равна Е.

181

испустившее γ – квант с энергией , получает импульс отдачи

поглотителя энергия кванта уменьшается на величину, равную(до малых высокого порядка). Таким образом, энергия кванта при его взаимодействии с невозбужденным ядром будет

этот квант, поскольку . Если бы каким-либо искусственным способом удалось увеличить энергию - квантов на 2Т, то наступило бы резонансное поглощение γ – квантов невозбужденными ядрами 191 r . В частности, один из способов основан на сдвиге частоты за счет эффекта Доплера, возникающем при сближении источника γ – квантов и поглотителя. При скорости сближения согласно формуле для продольного эффекта Доплера сдвиг частоты

(1 ) , что соответствует приращению энергии c c

кванта на . c

182

Энергия кванта, налетающего на ядро поглотителя равна2 . Если при этом 2 , то

cc

иядро поглощает такой квант.

5.273. Рассмотрим следующий опыт. На поверхности Земли имеются источник и поглотитель γ – квантов. Пусть

источник квантов начинаем двигать вверх с некоторой скоростью . Требуется подобрать такую скорость перемещения источника, чтобы на малой высоте l доплеровское и гравитационное смещения частоты γ – квантов полностью компенсировали друг друга. γ – Квант, обладая релятивистской

массой mr испытывает действие гравитационной силы c2

гравитационного центра. На пути dr распространения γ – кванта

Величина g имеет смысл ускорения свободного падения у

По условию r-R=l и l R. Учитывая, что r≈R, выражение (3)

Следовательно, гравитационный сдвиг частоты γ – квантов

При удалении источника от приемника со скоростью

На высоте l=20м скорость перемещения источника равна

184

=6,5 мкм/с.

5.274. Предварительно сделаем несколько замечаний. Энергия возбужденного состояния атомного ядра не является точно определенной величиной. Возбужденный энергетический уровень имеет конечную ширину Г, которую можно оценить по соотношению неопределенностей t . Положив =Г иt , где τ – среднее время жизни возбужденного состояния, по порядку величины составляющее примерно 10 10 с, для

ширины возбужденного уровня получим Г , что

соответствует частотному интервалу Г 1 . Если принять

энергию γ – кванта 50 кэВ, то относительная ширина

полосы квантовых возбужденных состояний Г 1,3 10 10 .

Это означает, что контур спектральной линии испущенных γ – квантов имеет чрезвычайно узкую относительную ширину.

Переходя в основное состояние, свободное неподвижное

возбужденное ядро испускает γ – квант с энергией ,

( )2

где Е – энергия перехода, - энергия отдачи ядра (mя -

2mяc2

масса ядра). При этом оказывается, что К>Г и, следовательно, резонансное поглощение γ – квантов ядрами поглотителя произойти не может.

И тем не менее, резонансное поглощение γ – излучения можно наблюдать. Это оказалось возможным только с ядрами, входящими в состав кристалла. В этом случае существует вероятность испускания γ – кванта ядром с отдачей, которое воспринимает не ядро, а весь кристалл в целом, не изменяя внутренней энергии кристалла. Масса кристалла несопоставимо

185

велика по сравнению с массой отдельного ядра, поэтому энергия отдачи кристалла практически равна нулю. В результате частота испущенного γ – кванта не смещается относительно резонансного значения, и этот γ – квант может быть поглощен другим таким же ядром, тоже входящим в состав кристалла.

Испускание или поглощение γ – квантов атомными ядрами, связанными в твердом теле, не сопровождающееся изменением внутренней энергии тела, называют эффектом Мессбауэра.

Исключительно малая ширина резонансных линий позволяет использовать эффект Мессбауэра для измерения малых сдвигов энергии γ – квантов, вызванных теми или иными воздействиями на излучающее ядро или γ – квант. В частности, с помощью этого эффекта было подтверждено гравитационное смещение спектральных линий.

Вусловиях задачи имеем: частотная ширина

минимальнаявысотаположенияисточникаγ–квантов равна 4,6 м.

186

6.ЯДЕРНЫЕ РЕАКЦИИ

5.275. Рассматривается упругое рассеяние -частицы с

классических представлений импульса и кинетической энергии. Введем следующие обозначения для масс, импульсов и

дейтрона. Здесь - угол рассеяния дейтрона в результате столкновения.

На основании за-кона сохранения импуль-са для проекций импуль-сов частиц на оси X и Y напишем следующие соотношения:

столкновения находятся далеко друг от друга, имеем ещё одно

5.278. При написании уравнений ядерных реакций в заданных случаях достаточно учесть сохранение заряда Z и числа