
Практика решения задач по физике. Часть 5. Квантовая физика. Евсюков В.А., Показаньева С.А
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
В.А. Евсюков С.А. Показаньева Е.П. Татьянина
ПРАКТИКА РЕШЕНИЯ ЗАДАЧ ПО ФИЗИКЕ
Часть 5 КВАНТОВАЯ ФИЗИКА
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2013
4
УДК 535.12(075)
Евсюков В.А. Практика решения задач по физике. Ч.5. Квантовая физика: учеб. пособие / В.А. Евсюков, С.А. Показаньева, Е.П. Татьянина. Воронеж: ФГБОУ ВПО «Воронежский государственныйтехническийуниверситет», 2013. 238с.
Учебное пособие посвящено практической части общей физики для высших учебных заведений. Содержит решения большого числа задач по вопросам корпускулярно-волнового дуализма электромагнитного излучения и частиц, основ квантовой механики, физики атома, молекулы и атомного ядра. Приведены необходимые теоретические сведения и исчерпывающие пояснения по решениюрассматриваемыхзадач.
Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по специальностям 160100.65, 160700.65, а также направлениям 151700.62, 151900.62, 221000.62, 230100.62, 230400.62, 151900.62, 131000.62, 140100.62, 221400.62, 150100.62, 150400.62, 210100.62, 221700.62, 222900.62, 223200.62.
Учебное пособие подготовлено в электронном виде в текстовом редакторе MS WORD XP, сохранено в формате pdf и содержитсяв файлеПРЗ_Ч5.pdf.
Табл. 7. Ил. 33.Библиогр.:5назв.
Рецензенты: кафедра общей физики Воронежского государственного университета (зав. кафедройд-рфиз.-мат. наук, проф.
В.В.Чернышев); д-р физ.-мат.наук, проф. Ю.Е. Калинин
©Евсюков В.А., Показаньева С.А., Татьянина Е.П., 2013
©Оформление. ФГБОУВПО«Воронежский государственный технический университет», 2013
5
ПРЕДИСЛОВИЕ
В предлагаемом учебном пособии рассматриваются задачи по вопросам корпускулярно-волнового дуализма электромагнитного излучения и микрочастиц, собственной квантовой механики, физики атома, молекулы и атомного ядра. Все задачи, о решении которых пойдет речь, заимствованы из сборника И.Е. Иродова «Задачи по общей физике», 2002 года издания. Представленные решения сохраняют нумерацию задач сборника.
Приведенные в пособии решения задач сопровождаются необходимыми рисунками, подробными и некоторыми обобщениями. Во многих случаях предварительно даются теоретические сведения по вопросам рассматриваемых задач.
Выпуск пособия адресован студентам физических и инженерно-технических специальностей. Пользование пособием может быть как систематическим, так и избирательным.
3

1. КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
5.1. |
Энергия кванта света с длиной волны |
равна |
|
= 2 |
⁄ |
. Количество квантов света (фотонов), испускаемых в |
|
|
|
||
единицу времени источником мощности Ρ на заданной длине
волны, равно |
плотность |
потока |
. |
При |
|
изотропном |
|||||
излучении |
|
источника |
световых |
частиц на |
|||||||
|
|
|
= |
|
= |
|
|
|
|
|
|
расстоянии |
от точечного источника2 |
|
|
|
|
|
|||||
Для P=10 Вт, |
=589 |
нм |
|
/(8 |
|
. |
|
||||
и =2,0 |
м |
плотность потока |
|||||||||
фотонов |
|
= |
см с |
⁄4 |
= |
|
|
) |
|
|
|
Установим связь между плотностью потока фотонов и их |
|||||||||||
|
= 6∙10 1/ |
|
∙ . |
|
|
|
|
|
|
|
|
концентрацией n. Количество фотонов, поступающих за время
|
|
|
|
|
|
|
|
элемента |
сферического слоя площадью |
|
|
и |
|||||||||||||||||||
|
|
в объём |
|
|
|
|
|||||||||||||||||||||||||
толщиной |
|
, равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
= ∙ = ∙ ⁄ = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Следовательно, концентрация фотонов |
⁄8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Отсюда |
|
|
= |
⁄ |
= ⁄ = |
|
|
|
|
|
|
|
|
|
|
|
(1). |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
получаем |
|
выражение |
для |
|
расстояния |
|
|
|
по |
|||||||||||||||
известному значению концентрации фотонов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Для |
= 100 |
= |
⁄(8м |
. |
) |
= |
⁄2 |
⁄2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
см |
|
|
|
|
|
|
|
|
где |
||||||||||||||||||||||
|
|
|
|
, = 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
5.2. Модуль импульса фотона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
= |
⁄ |
|
|
|
|
|
|
|
|
|
|
виде |
= |
|
|
. Поскольку |
||||||||||||||
|
|
|
|
-волновое число. В векторном |
|
= |
|
|
= |
|
|||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
= , |
|
|
||||||||||||||||
|
= 2 / |
, модуль импульса фотона можно представить |
|
в виде |
|||||||||||||||||||||||||||
|
. Постоянная Планка |
= 1,055∙10 |
|
|
Дж |
∙ |
с |
= 0,659∙ |
|||||||||||||||||||||||
|
= 2 / |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
эВ |
|
эВ. |
|
|
|
|
|
|
|
|
|
|
[ ] = [ ]⁄[ |
|
] = |
|
|
|
∙ |
⁄ |
|
= |
|||||||||
|
м с |
|
|
|
|
|
импульса |
|
эВ |
|
|||||||||||||||||||||
10 |
Размерность |
|
|
|
|
|
|
|
|
|
|
|
|
с м |
|
||||||||||||||||
|
|
⁄( |
⁄ ). |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Импульс фотона даже в единицах эВ |
с м весьма малая |
||||||||||
величина. |
В связи |
с |
этим импульсу |
фотона |
сопоставляют |
||||||
|
|
∙ ⁄ |
|
|
|||||||
величину |
|
( |
|
– скорость света) измеряемую в эВ. Тогда |
|||||||
|
импульс |
|
|
|
|
|
|
|
эВ |
||
реальный |
= |
|
|
|
с с и размерность |
|
|
с |
, где с – не |
||
единица измерения |
времени – секунда, а скорость света. |
||||||||||
|
= |
/ |
|
|
[ ] = |
|
= 0,25 мкм |
||||
Для фотонов с длинами волн |
= 0,50 мкм, |
|
|||||||||
и= 4,0 пм соответствующие импульсы в единицах эВ/с равны:
|
= |
с |
= |
|
∙ ∙ |
∙ , ∙ |
|
∙ |
эВ |
= 2,48 |
эВ |
|
|
|
|
|
|
|
с |
|
с |
|
|||||||||
|
|
эВ |
, |
∙ |
|
|
|
МэВ, . |
|
||||||
5.3. |
= 2 |
5 |
|
, |
= 1,25∙10 |
|
= 0,31 |
|
|
|
|
= |
|||
с |
|
|
с |
||||||||||||
|
Из |
релятивистского |
соотношения |
+ |
|||||||||||
|
|
|
|
|
|
||||||||||
=+ выражаем импульс электрона и равняем его
импульсу фотона 2 ⁄ : ( |
+ |
) |
= |
+ |
)⁄ |
|
|
Далее: |
||||||||
|
+2 |
= |
|
|
|
= |
|
|
( |
|
+2 |
|
. . |
Для |
||
|
|
|
|
|
|
|||||||||||
= 2 /МэВдлина |
|
|
= |
= |
( |
м |
) |
|
пм. |
|||||||
|
= 0,30 |
|
волны фотона |
|
|
|
|
|
|
|
|
|||||
|
= |
, ( , |
∙∙,∙ |
) |
/ , |
∙ |
= 2,0∙10 |
|
= 2,0 |
|
||||||
5.4.Импульсы по модулю электрона и фотона
соответственно |
равны |
|
э |
|
|
|
|
|
и |
|
|
. По |
|||||||
|
|
|
|
|
|
|
|
|
равенство |
|
|
|
|
|
|
|
|||
условию |
|
э |
|
|
. Отсюда |
1 − |
⁄ |
|
= 2 ⁄ |
, |
|||||||||
|
|
|
|
|
= |
⁄ |
|
||||||||||||
|
|
|
|
выражаем скорость электрона: |
⁄ |
|
= 2 ⁄ |
|
|||||||||||
из которого= |
|
|
|
|
|
|
|
|
⁄ |
1 − |
|
|
|||||||
|
= |
4 |
1 − |
|
|
( |
|
|
+4 ) = 4 |
||||||||||
|
|
|
|
||||||||||||||||
= |
|
|
пм |
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
( |
⁄ |
) |
|
|
|
|
|
|||||||
Для |
= 5,0 |
|
|
скорость электрона |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5

=  = 0,43
= 0,43
1+( |
0,91∙10 |
∙3∙10 |
∙5,0∙10 |
) |
||
2 |
|
м с |
|
|
||
|
∙1,05∙10 |
|
|
|||
5.5. Сначала= 1,3∙10 |
/ . |
|
импульса и энергии за |
|||
|
выразим |
потоки |
||||
единицу времени через нормальную площадку для фотонов
одной частоты . |
Импульс фотона |
|
|
|
|
|
|
|
|
|
|
|
, где |
|
||||||||||
Импульс, |
|
|
||||||||||||||||||||||
- энергия |
фотона. |
Отсюда |
|
=. |
переносимый |
|||||||||||||||||||
|
|
= |
= |
|
= |
|
|
|
||||||||||||||||
световым |
потоком |
за |
единицу |
времени через |
|
нормальную |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
площадку площади F, будет определяться суммой импульсов |
||||||||||||||||||||||||
фотонов, |
находящихся |
в |
объёме |
поток |
, т.е. |
|
|
через |
|
|
||||||||||||||
|
|
|
|
|
|
|
(1). При |
этом |
энергии |
ту же |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
⁄ |
= |
|
= |
|
площадку Φ |
|
|
|
(2). Сравнивая |
(1) и |
(2), |
получаем |
|||||||||||||||||
= ( ⁄ ) |
=э |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Φ |
э |
|
(3). Суммируя (или интегрируя) по всему |
спектру |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частот светового потока, получим то же соотношение (3). |
|
|
|
|||||||||||||||||||||
= |
|
|
⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.6. Давление электромагнитной волны при нормальном |
|||||||||||||||||||||
падении на плоскую поверхность тела равно |
= |
- |
|
|
|
|
, где |
|||||||||||||||||
|
|
|
|
- средняя |
плотность энергии волны, |
коэффициент |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1+ ) < |
|
> |
|
||||||
отражения. Плотность энергии в импульсе лазерного излучения |
|||||||||||||||||
< |
> |
⁄( |
) = |
/( |
) |
|
|
|
|
|
|
|
|
|
|||
< |
>= |
, |
где |
- |
пространственная |
длина |
|||||||||||
импульса, |
|
|
= |
|
⁄4 |
- площадь сечения пучка, - длительность |
|||||||||||
импульса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для |
Давление |
светового |
|
импульса |
на стенку |
в |
течение |
||||||||||
|
|
Дж |
|
|
|
мс |
|
|
|
= 4(1+ |
) |
⁄МПа . |
|||||
промежутка времени его действия равно |
|
= 5,0 |
= |
||||||||||||||
|
= 10 |
|
|
, |
= 0,13 |
|
, |
= 0,5 ; |
давление |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=50 атм.
5.7.Электромагнитное поле (волна) обладает импульсом. Для характеристики динамического воздействия электромагнитной волны на вещество вводят понятие плотности импульса
, определяемой импульсом электромагнитного поля в единице
6

объёма. Плотность импульса находится в определённой связи с другими характеристиками электромагнитной волны. Приводя эти соотношения, будем полагать, что электромагнитная волна распространяется в вакууме.
Плотность импульса волны в произвольной точке и
произвольный момент времени определим так: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
= ( |
|
) |
|
|
|
|
∙ |
|
|
|
= |
|
|
|
|
|
|
∙ |
|
|
|
|
= |
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
едс |
|
|
с |
|
|
с |
|
|
|
с |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||||||||||||||||||||||||||
Здесь |
ед -релятивистская |
|
|
масса |
|
единицы |
объёма |
поля с |
||||||||||||||||||||||||||||||||||||||||||||||||||||
объёмной( )плотностью энергии |
|
|
|
w |
|
|
в |
точке |
( |
, |
) |
; |
|
- волновой |
||||||||||||||||||||||||||||||||||||||||||||||
вектор, |
⁄ |
|
|
|
- |
|
|
|
орт |
|
|
|
|
|
|
направления |
|
|
|
распространения |
||||||||||||||||||||||||||||||||||||||||
электромагнитной |
волны. Среднее по времени значение |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
взаимную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
(2) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Учитывая |
|
|
|
|
ориентацию векторов |
|
|
|
и |
|||||||||||||||||||||||||||||||||||||||||||||||||||
соотношение |
|
|
|
|
|
|
|
|
< |
|
|
|
|
>= |
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
для плотности |
энергии |
||||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
, ( |
|
|
= |
|
|
|
|
|
= |
1) |
|
|||||||||||||||||||||||||||||||||||||
волны получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
. |
|
(3) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
энергии (вектор Пойтинга) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Плотность потока= |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= = |
|
|
|
∙ |
|
=E |
|
|
|
|
|
|
|
|
|
|
∙ |
|
= |
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
∙ |
|
= |
|
|
|
∙ |
|
= |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
имеем |
|
|
|
|
|
т е |
|
|
|
|
|
|
|
|
|
|
|
⁄ |
|
|
|
|
|
|
= |
⁄ |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
. |
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Отсюда с учётом (2) |
= |
|
|
|
|
∙ |
, |
|
|
|
. |
|
|
, а также∙ |
. |
|
|
|
|
по |
. |
|
(5) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Практически |
значимыми |
|
являются |
|
средние |
времени |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
величины |
< >= |
|
< |
|
|
|
|
|
> |
|
, < >= |
|
|
|
|
∙ |
|
. |
|
|
|
|
|
(6) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
В последующих действиях для упрощения символики угловые скобки средних величин опустим.
Для временного́ импульса электромагнитной волны в пространстве объёмом V динамический импульс
7
|
|
|
|
|
|
|
|
|
= |
|
= |
|
|
|
|
∙ |
|
= |
|
∙ |
|
, |
|
|
|
|
|
|
|
|
|
(7) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где - энергия цуга волны. Если импульс падающей волны |
||||||||||||||||||||||||||||||||||||||
обозначить через |
|
, то |
|
|
|
|
|
|
|
. Из соотношения (7) видно, что |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
векторы |
|
и |
|
имеют |
одно |
направление. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
= |
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
и ′′ |
|||||||||||
|
|
|
|
|
|
|
|
|
Теперь |
|
|
|
найдём |
|
импульсы |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
отражённой |
|
|
и проходящей волн. Для |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
составляющих |
|
векторов |
У, |
′ |
и |
|
′′ |
|
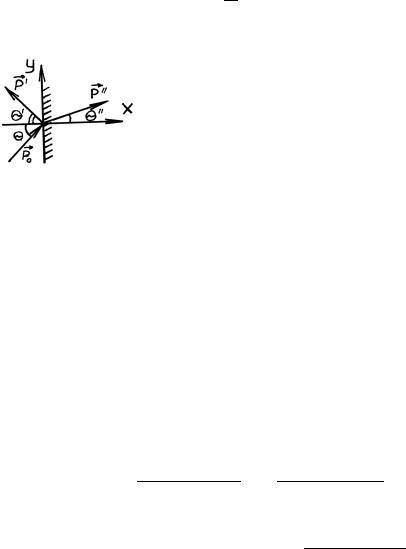
вдоль |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
координатных осей Х и |
(см. рис.) по с |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
закону |
|
|
сохранения |
|
импульса |
|
|
можем |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
написать: |
|
|
− |
|
|
|
|
|
|
|
, |
|
= |
; |
|
|
|
|
|
|
|||||||||
|
|
а) для х-составляющих |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
′′ |
|
′ |
|
|
|
|
′ |
|
|
|
|
|
|
||||||||
|
|
б) для у- |
составляющих |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
= |
= |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Из этих равенств следует: |
|
|
′ |
|
|
|
|
|
|
′′ |
|
|
|
′′. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
′′ |
= ( |
|
+ |
′ |
) |
|
, |
|
|
|
|
|
(8) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
′′ |
|
′ |
|
|
|
|
|
|
(9) |
||||||||||||
При возведении в квадрат |
равенств (8) и (9) и последующем их |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
− |
= ( |
|
|
− |
|
) |
|
. |
|
|
|
). |
|
|
= |
|||||||||||||||||||
сложении |
получим |
′′ |
= ( |
|
|
|
|
|
′ |
) |
|
|
|
|
|
|
|
+( |
++ |
′ |
|
|
||||||||||||||||
2 |
|
2 |
|
|
|
′ |
( |
2 |
|
|
2 |
) = |
|
|
2 |
|
|
|
′ |
2 |
|
|
|
|
|
′ |
|
|
|
|
|
|
||||||
0 + |
′ |
+2 |
|
|
|
− |
|
|
0 + |
|
|
|
+ +2 0 |
|
2 |
|
|
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(10) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Отношение энергий для отражённой и падающей волн есть |
|||||||||||||||||||||||||||||||||||||
коэффициент отражения. Поскольку импульс |
|
|
, |
то |
′ |
′′ |
|
|||||||||||||||||||||||||||||||
и, следовательно, равенство (10) |
|
можно |
представить как |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
~ |
|
|
|
|
|
= |
|
||||||||||||||||||||||||||||
|
(1+ |
|
+2′′= |
2 |
. Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||
Величину |
(11) |
|
|
1+ |
+2 |
|
|
|
2 |
|
|
= |
|
|
|
1+ |
+2 |
|
2 . |
|
величину |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
можно |
толковать |
|
как |
|
|
абсолютную |
|
|||||||||||||||||||||||
импульса р, переданного телу электромагнитной волной
некоторой протяжённости. Итак, = ( ⁄ ) 1+ +2 2 .
8
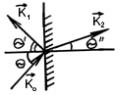
5.8. Рассматриваем плоскую монохроматическую световую волну как поток световых квантов, энергия и импульс
которых |
= |
и |
= |
. |
На |
плоскую |
поверхность тела единичной |
|
площади за 1с |
||||
падает |
|
|
квантов света (фотонов), где n – объёмная |
|||
фотонов (концентрация), |
- угол падения волны (см. |
|||||
плотность= |
cos |
|
|
|
|
|
рис.). При этом на данную площадку падает энергия = ∙ =
cos и соответствующий механический импульс
|
= |
∙ = |
|
cos |
∙ = |
cos ∙ |
|
|
|
|
|
||||||
где |
− |
орт |
волнового вектора . |
|
, |
|||
Давление |
света |
|
, как |
действие |
нормальной силы на |
|||
единичную площадку при полном его поглощении равно
изменению |
|
импульса |
|
= |
|
|
= . |
При, |
наличиит.е. |
|||||
= cos = ( |
cos |
)cos |
|
|
cos |
|
|
|
|
|||||
отражения |
волны |
давление |
|
) |
согласно |
закону сохранения |
||||||||
Концентрацию |
|
= (1+ |
= (1+ |
) |
cos |
(1). |
||||||||
импульса будет равно |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
фотонов в падающей волне найдём по |
||||||||||||
заданной плотности потока энергии (интенсивности): |
(3) |
|||||||||||||
=< |
>= ( |
) |
= |
с |
|
= |
|
⁄( |
). |
|
||||
Подставляя (2) в (1), получим |
|
= (1+ |
) |
|
|
cos . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Вобычной символике, давление = .
5.9.Результирующая сила светового давления, испытываемая шаром, равна произведению давления света и
площади поперечного большого сечения шара, т.е. |
|
, |
|||||||
где |
- радиус шара. |
Поверхность шара является |
=идеально∙ |
||||||
отражающей, |
= |
|
. Согласно формуле (3) задачи 5.8. при |
|
|||||
|
|
= |
|
|
|
|
|
|
|
получаем |
|
= 1 |
|
|
. |
|
= 0 |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
9 |
|
|
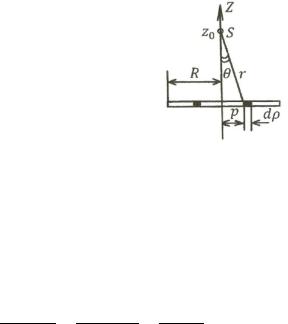
5.10.Здесь также воспользуемся
формулой (3) задачи |
5.8., |
учитывая |
что |
||
В= 1 |
: давление света |
= (2 |
⁄ )cos |
. |
|
|
|
|
|
||
рассматриваемом случае |
интенсивность |
||||
светового потока |
|
|
, где |
- |
|
|
источника света, |
а - |
|||
мощность точечного= |
⁄(4 |
) |
|
|
|
расстояние до выбранной точки заданной поверхности.
Пространственное положение источника света и круглой пластинки показано на рисунке. Сила давления на кольцевой
элемент, |
поверхности круглой пластинки |
как= ∙ |
= (2 ⁄ )cos |
и∙ |
|||||||||||||||
где |
- радиус |
кольца. Так |
|||||||||||||||||
2 |
|
|
, то |
|
|
|
|
|
|
|
|
|
|
cos. |
= / |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
+ |
= |
|
= ( |
) |
|
|||||||||||||
= |
|
|
|
|
|
|
|
|
|
||||||||||
Результирующая сила светового давления на пластинку равна |
|
||||||||||||||||||
|
|
|
= |
|
∫ |
( |
) |
= |
( |
) |
= |
( |
) |
. |
|
||||
|
|
|
|
|
|||||||||||||||
5.11. Читателю имеет смысл сначала ознакомиться с решением задачи 3.280, в котором установлена связь между частотами падающей электромагнитной волны и отражённой от движущегося зеркала. С квантовой точки зрения электромагнитная волна рассматривается как потом фотонов с определённым их пространственно-временным распределением.
В данной задаче объектом рассмотрения является отдельный фотон, характеризуемый определёнными величинами: частотой
энергией |
= |
и |
импульсом |
= |
. Частоту кванта |
|
частоте |
||||
электромагнитного, |
поля |
равняют |
соответствующей |
||
электромагнитной волны. В связи с этим, релятивистский закон преобразования частоты волны и отдельного фотона при переходе из одной системы отсчёта в другую один и тот же.
Приведём формулы (1) и (3) задачи 3.280:
10
