4. Точностной анализ оборудования и механизмов

Точность станка предопределяет точность обработанных на нем деталей. По источникам возник­новения отклонений от установленных норм и характеру все ошибки станка, влияющие на погрешности обработан­ных изделий, условно разделяют на несколько групп. Основные из них таковы: геометрическая точность, кинематическая точность, жесткость станков, позиционирование, виброустойчивость, автоколебания, теплостойкость и другие.

Рассмотрим причины возникновения погрешностей в узлах и системах оборудования, определяющих и влияющих на точности обработки. При этом отметим, что при отсутствии внешних воздействий, геометрическая точность зависит от ошибок соединений элементов узлов и влияет на точность взаимного расположения узлов станка, то есть геометрическая точность главным образом зависит от точности изготовления соединений базовых деталей и от качества сборки станка. Поэтому на погрешности в расположении основ­ных узлов станка существуют нормы. Нормы на допустимые для данного станка геометрические погреш­ности зависят от требуемой точности изготовления на нем деталей. Соответствие установленным нормам проверяют как для нового станка, так и периодически при его эксплуатации.

Сложные движения деталей и узлов, особенно зубообрабатывающих, резьбонарезных и других станков, где осуществляется сложная контурная обработка, требуют согласования скоростей нескольких простых движений. Так появляется необходимость выделить особое значение кинематической точности. Нарушение согласованных движений нарушает правиль­ность заданной траектории движения инструмента относительно за­готовки и искажает тем самым форму обрабатываемой поверхности.

Следующий важный показатель - это жесткость станков, которая характеризует их свойство противостоять появлению упругих в системе перемещений, возникающих под действием постоянных или медленно изменяющихся во времени силовых воздействий. Жест­кость это отношение силы к соответствующей упругой деформации в том же направлении. Величину, обратную жесткости, называют податливостью. Податливость сложной системы из набора упругих элементов, работающих последовательно, равна сумме податливостей этих элементов.

Отметим, что жесткость станка (его несущей системы), влияющая на точности обработки, должна обеспечить упругое перемещение между инструментом и заготовкой в заданных пределах. Жесткость и соответственно податливость базовых деталей станка из чугуна или стали подчиняются закону Гука и для каждой детали есть вели­чины постоянные. Близка к постоянному значению жесткость несущих систем станка при большом числе упругих деталей. Жесткость же большинства отдельных соединений, таких как неподвижные стыки, направляющие, подшипники качения и сколь­жения, не является постоянной величиной вследствие отсутствия прямой пропорциональности между силой и упругим перемещением, поэтому на них следует обращать особое внимание.

4.1. Основные источники погрешностей

При проектировании станков и их механизмов одной из основных задач является, как правило, обеспечение требуемой точности функционирования системы, ведь всякий реально созданный станок отличается от идеальных прототипов, которые наилучшим образом могут решать поставленные перед ними задачи. Для большинства механических систем эти отличия обусловлены применением упрощенной или усложненной кинематической схемы, возникающими погрешностями изготовления или монтажа, вызывающими деформацию звеньев и контактные деформации, влиянием сил трения, изнашиванием поверхностей, влиянием эксплуатационных нагрузок и т. п.

Все возможные погрешности, вызывающие неточности работы механизмов, классифицируют по причинам, вследствие которых они возникают. Различают погрешности следующих типов /13/.

1. Методические, возникающие вследствие различия между действительным и требуемым законами движения узлов и ведомого звена. Методические погрешности часто называют погрешностями схемы; они появляются в результате изменения кинематической схемы или технологии изготовления и сборки объекта.

2. Технологические, возникающие при изготовлении и сборке механизмов; к их числу относятся погрешности размеров (линейные и угловые), геометрических форм и расположения рабочих поверхностей. Первичные технологические погрешности делятся на скалярные (погрешности размеров) и векторные (погрешности от зазоров, эксцентриситетов и т. п.).

3. Эксплуатационные, возникающие при эксплуатации механизмов в результате силовых и температурных деформаций звеньев, вибраций, изнашивания деталей и т. п.

Погрешность ∆y определяется как разность между идеальной y_ид = f(x) и действительной y_д = f₁(x) функциями перемещения механизма (рис. 57).

Погрешности в зависимости от закономерности их появления разделяют на случайные и систематические.

Случайная погрешность при повторных измерениях одной и той же величины изменяется случайным образом. Присутствие случайных погрешностей можно легко установить несколькими повторными действиями при неизменных условиях эксперимента. Причинами появления случайных погрешностей являются неконтролируемые непрерывные изменения всех факторов и условий, влияющих на результаты обработки или измерений. Случайные погрешности неустранимы, но их влияние может быть уменьшено путем учета соответствующей коррекции.

Рис. 57. Функции перемещения идеального и действительного механизмов

В узлах с механическими, гидравлическими и другими приводами основными причинами появления случайных погрешностей являются зазоры в передачах, трение в шарнирах, непостоянство усилий и деформаций, температур и т. п.

Систематическая погрешность остается постоянной или закономерно изменяется. Методические погрешности, как правило, относятся к систематическим. Часто систематическими являются также температурные погрешности. Систематическая погрешность может быть учтена введением тех или иных поправок.

По закономерности появления систематические погрешности могут быть разделены на четыре группы: 1) постоянные (например, погрешность закрепления заготовки); 2) возрастающие, увеличивающиеся с ростом измеряемой величины (например, температурные погрешности при измерении длины детали); 3) периодические (например, погрешность, связанная с эксцентриситетом звена); 4) изменяющиеся по сложному закону (например, при использовании упрощенных физических зависимостей вместо точных, но более сложных).

Невозможность абсолютно точно стабилизировать влияющие факторы приводит к тому, что большинство характеристик работы и настройки станка являются вероятностными величинами и могут быть оценены лишь в результате их статистической обработки.

Рассмотрим случайные величины и их характеристики. Теория вероятностей описывает математические модели случайных событий. Случайным считается такое событие, которое в одинаковых условиях может произойти или не произойти. Если при выполнении N раз некоторых условий случайное событие А осуществилось N (А) раз, то отношение N (A)/N называют относительной частотой события А. Для случайных событий при достаточно больших N относительная частота обладает свойством устойчивости, т. е. находится около одного и того же числа. Это число называют вероятностью события А и обозначают Р (А). Если всем возможным событиям А, В, С, ..., которые могут осуществиться при некоторых условиях, поставить в соответствие некоторые величины х₁ х₂, х₃, ..., то считается, что этим событиям соответствуют различные значения случайной величины X. Поэтому в качестве случайного события можно рассматривать принятие случайной величиной X каких-либо из ее возможных значений.

Случайная величина X называется дискретной, если множество ее возможных значений представляет собой конечную или бесконечную последовательность чисел x₁ x₂, ... и если каждое событие X = x_i является случайным, т. е. имеет определенную вероятность.

Основной характеристикой дискретной случайной величины является закон распределения вероятностей, устанавливающий связь между возможными значениями случайной величины и соответствующими вероятностями. Закон распределения может быть задан аналитически, в виде графика (рис. 58) или таблицы.

Рис.58. График распределения дискретных случайных величин

Случайная величина, возможные значения которой сплошь заполняют некоторый интервал, называется непрерывной. Для непрерывной случайной величины имеет смысл рассматривать только такое событие, как попадание в интервал, поскольку вероятность попадания непрерывной случайной величины в любую заранее заданную точку равна нулю. Поэтому для ее характеристики используется понятие плотности вероятности.

Плотностью вероятности р называют предел отношения вероятности того, что возможные значения случайной величины находятся в определенном интервале, к значению этого интервала:

, ₍₆₇₎

где х - нижнее предельное значение интервала; х+∆х - верхнее предельное значение интервала; ∆х - значение интервала.

Представив графически, рис.59, плотность распределения непрерывной случайной величины, видим, что если случайная величина находится в интервале ∆х, то соответствующая вероятность такова

если в интервале (а, b), то она уже

. (68)

В этом случае площадь, ограниченная кривой и ординатами в точках а и b, будет численно равна вероятности нахождения случайной величины в этих пределах. Для пределов от +∞ до -∞ имеем:

.

Рис. 59. График плотности распределения вероятностей

непрерывных случайных величин

Площадь, ограниченная кривой плотности распределения и осью абсцисс в пределах ± ∞, определяет достоверное событие и всегда равна единице. Помимо плотности распределения вероятностей, для непрерывных случайных величин используют еще три способа аналитического описания законов распределения:

функция распределения вероятностей случайной величины, равной вероятности того, что случайная величина примет значение, не большее чем х:

; (69)

дополнительная функция распределения

; (70)

функция интенсивности

. (71)

Графики перечисленных функций (0 < X < _∞) для экспоненциального и нормального распределений и распределения Вейбулла (для последнего случая приведены по две кривых каждой функции, соответствующих различным сочетаниям параметров) показаны на рис. 60.

Функции р (х), F (x), G (х) и Н (х) однозначно пересчитываются одна в другую, поэтому принципиально они могут быть использованы для описания законов распределения. Однако некоторые специфические особенности этих функций делают каждую из них более или менее удобной для решения тех или иных задач.

Функции F (х) и G (х) позволяют непосредственно отсчитывать значения вероятностей попадания случайной величины в заданные интервалы. В то же время эти функции для любых законов распределения монотонны, что скрадывает специфические черты различных законов распределения. Плотность р(х) наиболее ярко отображает основные особенности закона распределения: расположение области возможных значений на оси, наличие и расположение наиболее вероятных значений, степень рассеяния, симметричность и т. п. В связи с этим она наиболее удобна для наглядного представления свойств случайной величины. Функция интенсивности Н (х) относительно редко используется для описания законов распределения, причем главным образом в теории надежности.

Функции, описывающие закон распределения, не всегда удобны для практического пользования. В связи с этим широкое распространение получили так называемые числовые характеристики случайных величин, которые описывают не все свойства случайной величины, но просты и удобны в инженерной практике.

Рис. 60. Графики функций р (х), F (х), G (х) и H(х) для разных законов распределения: а - экспоненциального;

б - нормального; в - распределения Вейбулла

Среди них можно выделить h-квантиль, начальные и центральные моменты случайной величины, h-квантилем x_h называется такое значение случайной величины, которому соответствует значение функции распределения случайной величины, равное h:

.

Начальным моментом v-гo порядка называется интеграл

.

Наиболее широко используется начальный момент 1-го порядка

, (72)

называемый математическим ожиданием случайной величины (средним арифметическим или центром группирования).

Центральный момент v-гo порядка определяется выражением

.

Важную роль играет второй центральный момент

, (73)

называемый дисперсией и характеризующий степень рассеяния случайной величины. Чтобы избавиться от неудобств размерности , которая, как видно из выражения (73), равна квадрату размерности X, для характеристики рассеяния случайной величины часто используют среднее квадратичное отклонение

. (74)

Для характеристики зоны рассеивания вводят понятие предельного отклонения случайной величины.

Предельным отклонением называют такое отклонение случайной величины от среднего арифметического, за пределами которого по обе стороны находятся отклонения с заданной вероятностью появления. Предельные отклонения выражают в долях среднего квадратичного отклонения. Для симметричных законов распределения

, (75)

где А - коэффициент предельного отклонения, зависящий от формы кривой распределения и допустимой вероятности выхода значения случайной величины за принятые пределы.

Числовые характеристики случайных величин выполняют весьма важную роль. В частности, их используют при переходе от экспериментально определенных значений распределения к математическим моделям распределения, более удобным в исследовании. Все математические модели или законы могут быть представлены в следующем общем виде:

p = p (x₁, p₁, p₂, p₃, …, p_n,),

где p₁, p₂, p₃, …, p_n - параметры закона распределения; в зависимости от их числа различают одно-, двух-, трех- и n-параметрические распределения.

На практике наиболее часто встречаются следующие законы распределения случайных величин.

1. Распределение по закону равной вероятности (рис. 61). Закон описывает распределение результатов округления, его используют при оценке погрешностей, вызванных эксцентриситетами, перекосами осей за счет зазоров и т. д.

Среднее арифметическое значение случайной величины равно

.

а) б)

Рис. 61. Графики распределения случайных величин по закону равной вероятности (а) и Симпсона (б)

Среднее квадратическое отклонение

.

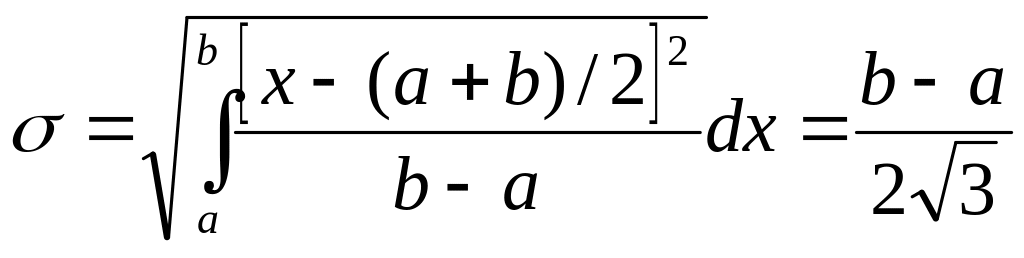Коэффициент предельного отклонения равен

.

Следовательно, для закона равной вероятности

.

2. Распределение по закону Симпсона. Этот закон применим при сложении двух случайных величин, каждая из которых следует закону равной вероятности (рис. 61).

Среднее арифметическое значение

.

Среднее квадратическое отклонение

.

Тогда коэффициент предельного отклонения

.

Следовательно, для распределения по закону Симпсона

.

3. Экспоненциальное распределение (см. рис. 60, а). Этот закон широко используется в теории надежности, характеризуется плотностью распределения вероятности вида

p(x, p₁) = .

Функция экспоненциального распределения вероятностей случайной величины имеет вид

,

функция интенсивности

H (x, p₁) = p₁.

Среднее арифметическое значение равно среднему квадратическому отклонению:

.

4. Распределение Эрланга. Этому закону соответствуют следующие функции

_{; ;}

_{причем .}

5. Распределение по нормальному закону (закону Гаусса). Такое распределение непрерывных случайных величин обусловливается одновременным действием большого числа независимых и однородных по своему влиянию факторов, причем ни один из факторов не является доминирующим.

Большинство случайных величин подчиняется закону Гаусса, поэтому закон нормального распределения имеет первостепенное значение при точностных расчетах и оценках работы механизмов.

Функция плотности распределения закона Гаусса имеет вид

_. (76)

Среднее арифметическое случайной величины m = p₁. Среднее квадратическое отклонение σ = p₂.

Закон нормального распределения графически изображается колоколообразной кривой (см. рис. 60, б) с ветвями-асимптотами к оси х и модой, соответствующей среднему арифметическому значению

_.

Нетрудно доказать, что точка перегиба на ветвях находится на расстояниях ±σ относительно т.

При рассмотрении кривой можно заметить, что среднее арифметическое значение случайной величины имеет максимальную плотность вероятности; кривая симметрична относительно ординаты т, поэтому одинаковые отклонения от среднего арифметического с разными знаками равновероятны; ветви кривой асимптотически приближаются к оси х, следовательно, большие отклонения от среднего арифметического менее вероятны.

Для практических расчетов удобнее считать, что центр группирования совпадает с началом координат и величина х выражается в долях от среднего квадратического. В этом случае, если обозначить (x-m)/σ = z, плотность нормального распределения вероятностей случайной величины .

Вероятность нахождения случайной величины в интервале ab

₍₇₇₎

где z₁ = (b - m)/σ; z₂ = (а - m)/σ_.

Выражение в элементарных функциях не интегрируется, поэтому для подсчета интегралов составлены таблицы значений функции

,

называемой функцией Лапласа.

Тогда выражение (41) примет вид:

.

Рис. 62. График плотности распределения вероятностей по закону Гаусса: 1 — площадь, определяемая функцией F (b/σ);

2 — площадь, определяемая функцией F (а/ σ)

На практике принято считать, что размер интервала ± 3σ практически полностью определяет собой диапазон рассеивания.

При этом коэффициент предельного отклонения А=∆/σ=3. Следовательно, для закона нормального распределения ∆= ± 3σ_.

Необходимо отметить, что иногда приходится сталкиваться с тем, что одна какая-то случайная величина х является суммой двух независимых случайных величин x₁ и x₂, каждая из которых имеет определенный закон распределения. Не рассматривая подробно теорию композиций, можно отметить:

композиция двух законов нормального распределения дает закон нормального распределения с дисперсией, равной сумме дисперсий отдельных распределений; в этом случае среднее квадратичное отклонение

;

композиция двух законов равной вероятности дает закон Симпсона с дисперсией, равной сумме дисперсий отдельных законов;

композиция двух законов Симпсона, смешанные композиции из трех законов и более с достаточной степенью точности приводят к закону нормального распределения. Это положение еще раз подтверждает, что при наличии большого числа факторов, влияющих на случайную величину, распределение последней подчиняется закону Гаусса.

6. Логарифмически-нормальное распределение. Такое распределение часто используют для описания долговечности материалов в условиях усталостного нагружения. Оно характеризуется следующими функциями распределения:

,

,

.

7. Гамма-распределение:

,

,

где - неполная гамма-функция

.

В этом случае

.

При p₁= 1 гамма-распределение переходит в экспоненциальное; при p₁= 1, 2, 3, ..., k - в гамма-распределение Эрланга k-гo порядка. Частным случаем гамма-распределения (при p₁= n/2 и p₂ = 1/2) является также распределение x².

8. Трехпараметрическое распределение Вейбулла:

,

,

.

Частным случаем распределения Вейбулла является экспоненциальное распределение (при p₁= 0 и p₂= 1).

Приведенные выше законы распределения представляют собой удобные в аналитическом исследовании математические модели, оказывающиеся во многих случаях достаточно близкими к реальным законам распределения случайных величин, исследуемых в тех или иных технических задачах.

В связи с этим важной задачей, имеющей большое практическое значение, является подбор подходящей математической модели закона распределения для описания случайной величины, заданной рядом экспериментально полученных данных, которые принято называть реализациями случайной величины.

Набор х₁,х₂, ..., x_h h-реализаций называют простой статистической совокупностью. Эту совокупность удобно записывать в виде таблицы: в первом столбце таблицы указывается номер i реализации (от 1 до h), во втором — соответствующие значения . В целях более наглядного отображения исходного статистического материала его представляют в виде упорядоченной статистической совокупности или вариационного ряда, где номера (от 1 до h) присваиваются реализациям в порядке возрастания их значений. При h > 50 работать с таблицей упорядоченной статистической совокупности неудобно. В этих случаях исходный статистический материал подвергается предварительной обработке. Весь диапазон значений x_i (от х₁ до x_h) разбивают на r интервалов:

_{y1 = (x1, x2), y2 = (x2, x3), …, yj = (xj, xj+1), …, yr = (xr, xr+1)}

(в общем случае интервалы y_j могут быть неравны). Затем подсчитывают число реализаций h_j, попавших в каждый интервал, и вычисляют частоту η_j попадания в j интервал по формуле

η_j = h_j/h.

Нетрудно видеть, что всегда имеют место равенства

.

Далее строят таблицу с четырьмя столбцами (табл. 8). Такое представление исходных данных называется статистическим рядом.

Для наглядного представления статистического ряда строят графики статистических функций распределения случайной величины.

Для построения статистической функции плотности распределения p^*(x) (здесь и далее статистические функции распределения и статистические числовые характеристики распределений обозначены соответствующим символом со знаком ^*) на горизонтальной оси строят интервалы статистического ряда.

Таблица 8

Обработка опытных статистических данных

№ интервала	Предельные размеры интервала	Средний размер интервала	Частота интервала
1	x1 – x2
2	x2 – x3
3	x3 – x4
.	.	.	.
.	.	.	.
.	.	.	.
r	xr – xr+1

Рис. 63. Графическое изображение статистических законов распределения: 1 - гистограмма распределения;

2 - полигон распределения

На каждом интервале y_j как на основании строят прямоугольник, высота которого l_j определяется как отношение частоты к ширине интервала:

Совокупность прямоугольников представляет собой гистограмму распределения (кривая 1 на рис. 63). Нетрудно видеть, что сумма площадей всех прямоугольников гистограммы

.

Если по оси абсцисс откладывать средние арифметические размеры интервалов …, то полученную ломаную называют полигоном распределения (см. кривую 2 на рис. 63).Статистический ряд позволяет также построить статистический эквивалент интегральной функции распределения F^*(x) На основе графиков статистических функций распределения легко найти статистические эквиваленты точечных и интервальных характеристик.

Для статистического математического ожидания (называемого часто статистическим средним) случайной величины имеем

,

для статистической дисперсии

, где .