3.2. Спектр атома водорода

Спектр испускания электромагнитных волн отдельными атомами представляет собой набор спектральных линий, соответствующих излучениям с определенной длиной волны (частотой), и поэтому называется линейчатым. Изучение линейчатых спектров испускания атомов послужило ключом к познанию строения атомов. Прежде всего, было замечено, что линии в спектрах атомов расположены не беспорядочно, а объединяются в группы, или, как их называют, серии линий. Отчетливее всего это обнаруживается в спектре простейшего атома – водорода. Расстояние между спектральными линиями закономерно убывает по мере перехода от более длинных волн к более коротким волнам.

Первые успехи были получены при изучении спектра водорода в 1885 г. И. Бальмером, который показал, что длины волн, соответствующие спектральным линиям видимого участка спектра водорода, определяются формулой:

 = ₀ , n = 3, 4, 5, ,

где ₀ = 367,56 нм – некоторая постоянная. Спектральные линии, определенные этой формулой, назвали серией Бальмера. Если перейти к частоте, получается формула Бальмера:

 = R_ ( ), n = 3, 4, 5, ,

где R_ = 2,0710¹⁶ с^-1 – постоянная Ридберга (для циклической частоты). В спектроскопии принято характеризовать спектральные линии величиной, обратной длине волны:

= ,

где называют волновым числом (не путать с волновым числом k = = ). Формула Бальмера для волнового числа принимает вид:

= R_ ( ), n = 3, 4, 5, ,

где R_ = 10973731, 77 м^-1 – постоянная Ридберга (для обратной длины волны).

Дальнейшие исследования показали, что в спектре водорода имеется еще несколько серий. В ультрафиолетовой части спектра находится серия Лаймана. Остальные серии лежат в инфракрасной области. Линии этих серий могут быть представлены формулами:

серия Лаймана  = R_ ( ), n = 2, 3, 4, ,

серия Пашена  = R_ ( ), n = 4, 5, 6, ,

серия Брэккета  = R_ ( ), n = 5, 6, 7, ,

серия Пфунда  = R_ ( ), n = 6, 7, 8, .

Частоту всех линий спектра атома водорода (рис. 33) можно представить обобщенной формулой Бальмера:

 = R_ ( ),

где при заданном m число n принимает целочисленные значения, начиная с m +1.

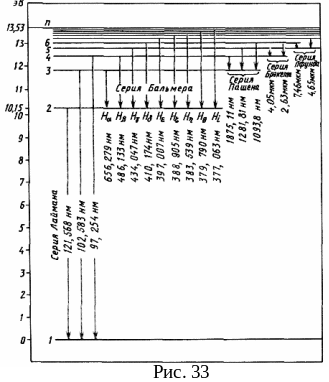
При возрастании n частота линии в каждой серии стремится к предельному значению , которое называется границей серии. Частота, соответствующая границе серии, называется термом и обозначается Т_m:

Т_m = (для водорода).

Терм для изоэлектронного водороду иона равен: Т_m = Z .

Механизм возникновения линейчатых спектров и смысл целых чисел, входящих в формулы спектральных серий, однако оставались непонятными. Решить эту проблему удалось только Бору.

Бор предложил общий принцип объяснения происхождения атомных спектров, вывел теоретически точные количественные закономерности распределения линий в спектрах атома водорода и водородоподобных ионов (Не⁺, Li⁺⁺, Be³⁺, C⁵⁺). Водородоподобными ионами называются атомы, у которых удалены все электроны кроме одного, находящегося в поле ядра с положительным зарядом Ze, где Z – порядковый номер элемента в периодической таблице, е – элементарный заряд.

Положение линий в линейчатом спектре испускания вещества точно совпадает с положением линий в линейчатом спектре поглощения этого же вещества. У атомов разных химических элементов электрический заряд атомных ядер имеет различное значение, поэтому стационарные состояния их различны, что приводит к различиям в их линейчатых спектрах испускания и поглощения.

Атом водорода в классической физике. Согласно полуклассической теории Бора, движение электрона вокруг ядра в стационарных состояниях определяется законами классической механики, для описания же процессов перехода атома из одного стационарного состояния в другое необходимо пользоваться квантовыми представлениями.

Для движения электрона по круговой орбите с радиусом r_n в рамках модели атома Резерфорда из уравнения движения (кулоновская сила притяжения электрона к ядру атома уравновешивается центробежной силой отталкивания электрона от ядра) F_кул = m_еа_ц.с. и правила квантования орбит (второй постулат) m_ev_nr_n = nћ, после подстановок выражений для кулоновской силы F_кул = и центростремительного ускорения а_ц.с = v_n²/r_n, получается соотношение:

= m_еа_ц.с,

из которого можно выразить скорость электрона на n – й орбите и ее радиус:

v_n = , r_n = .

Минимальное возможное значение орбитального момента импульса электрона равно (при n = 1) m_ev₁r₁ = ћ = = 1,05510^-34 Джс. Радиус первой круговой стационарной орбиты, называемый боровским радиусом, равен

r₁ = 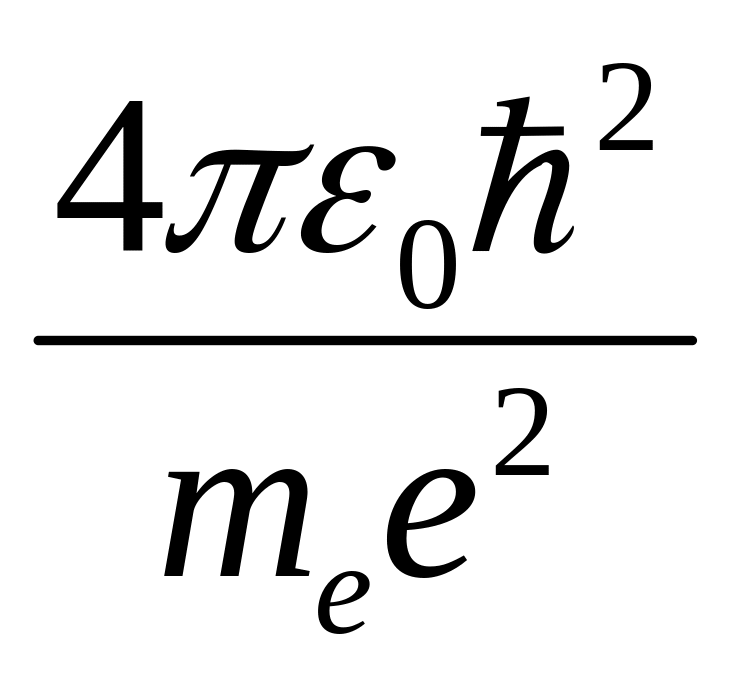= 5,2910^-11 м.

Радиусы последующих стационарных орбит вычисляются для n = 2, 3,  .

Потенциальная энергия Е_р электростатического взаимодействия электрона с ядром в атоме водорода определяется формулой:

Е_р = - .

Кинетическая энергия электрона при движении по круговой орбите равна:

Е_k = = .

Полная энергия Е системы из атомного ядра и электрона, обращающегося по круговой орбите радиусом r, равна:

Е = Е_р + Е_k = - .

Подставляя выражение для радиуса r_n, получаем значение полной энергии Е_n атома водорода в данном стационарном состоянии:

Е_n = -  .

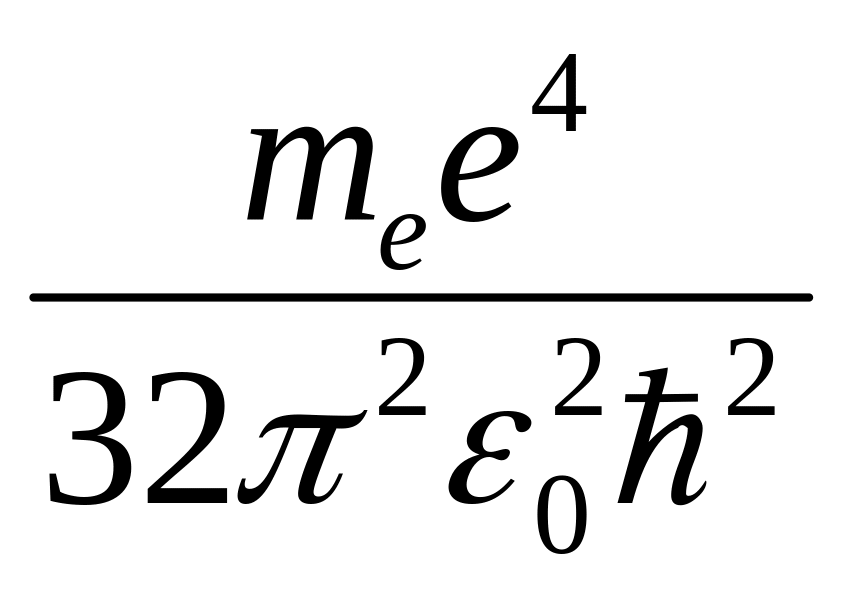
При n = 1 (основное состояние атома водорода) E₁ = -13,6 эВ

При переходе электрона со стационарной круговой орбиты радиусом r_n на стационарную круговую орбиту радиусом r_m изменение энергии атома равно:

∆Е = Е_n – Е_m =  ( ).

Частота кванта _mn, соответствующего этому переходу, равна:

_mn = = =  ( ),

где величина R_ = = 3,2910¹⁵ с^-1 – постоянная Ридберга (для частоты). С учетом этого формула принимает вид:

_mn = R_ ( ),

что согласуется с обобщенной формулой Бальмера, при замене в ней частоты  на , а постоянной Ридберга R_ на величину R_ = 2R_.

Расчет спектра водорода был серьезным успехом боровской теории, основные положения которой экспериментально были подтверждены в 1913 г. опытами Дж. Франка и Г. Герца по установлению факта дискретности энергетических состояний атома при исследовании столкновений электронов с атомами ртути. Однако, добившись определенного успеха в объяснении спектра атома водорода, теория Бора не позволила вычислить интенсивности излучения тех или иных частот в спектре атома водорода.

Дальнейшее развитие физики показало, что трудности теории Бора были не случайными, так как боровская теория не являлась последовательной и идея квантованности энергетических состояний атома не являлась ее следствием, а формулировалась в качестве постулата. Теория Бора не описывала и тонкую структуру водородоподобных атомов, а также свойства многоэлектронных атомов, начиная с атома гелия.