2.2. Классификация уравнений

С помощью замены переменных уравнение второго порядка

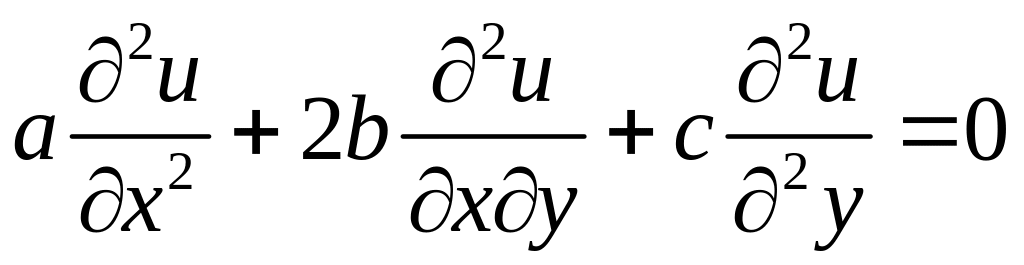(2.6)

сводится к одному из простейших уравнений. Полагая, что коэффициент , введем новые независимые переменные: где произвольные, но различные _числа (иначе не будут взаимно независимые функции)_{. Так как}

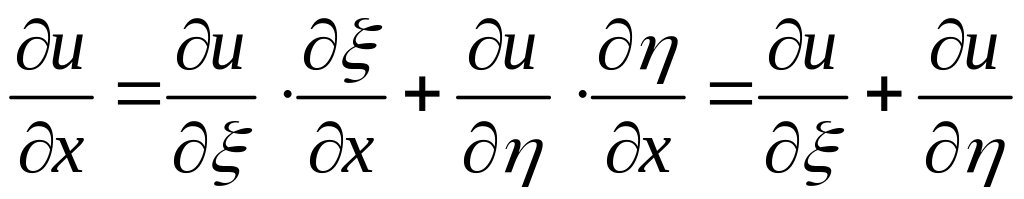_и

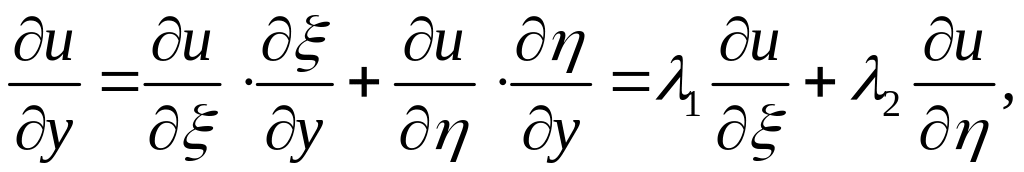
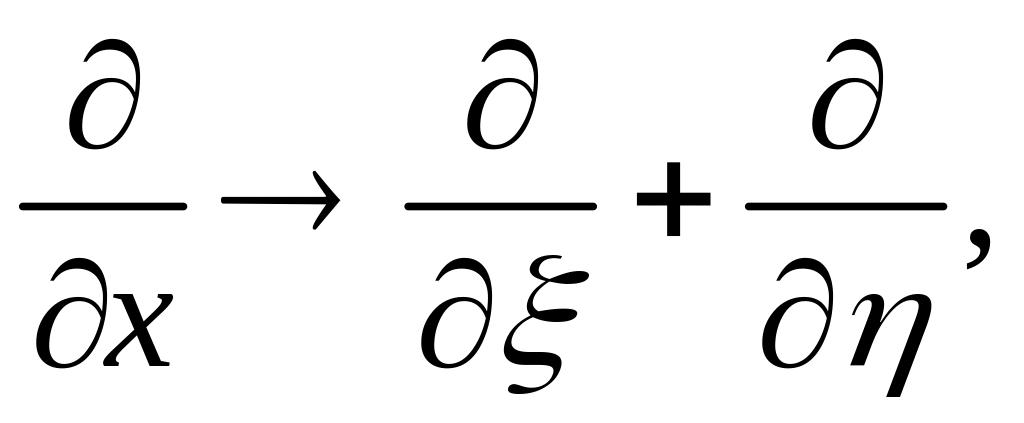
то имеет место соответствие 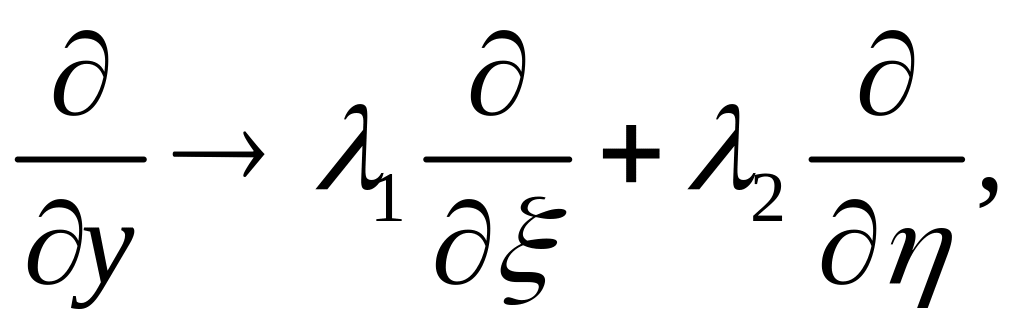поэтому

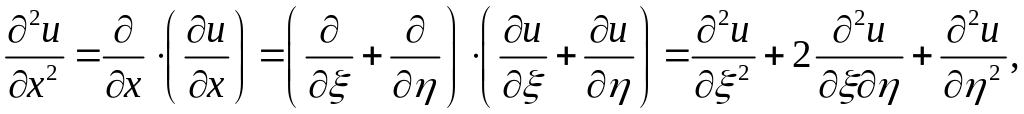
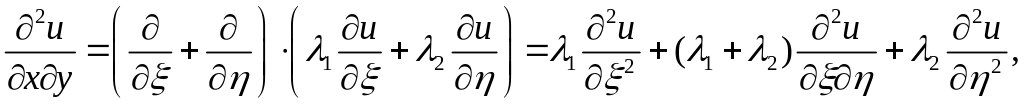
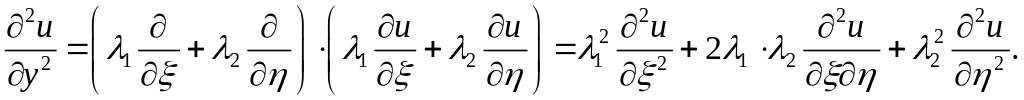
Умножим эти вторые производные соответственно на a, 2b и c, а затем их сложим, тогда левая часть уравнения (2.6) примет вид

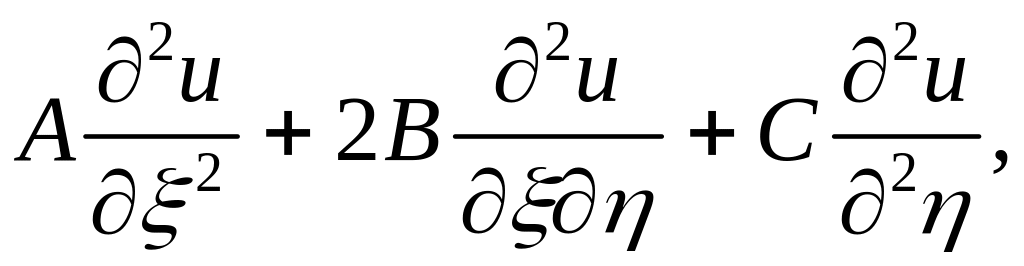
где

Рассмотрим вспомогательное квадратное уравнение

Его корнями являются 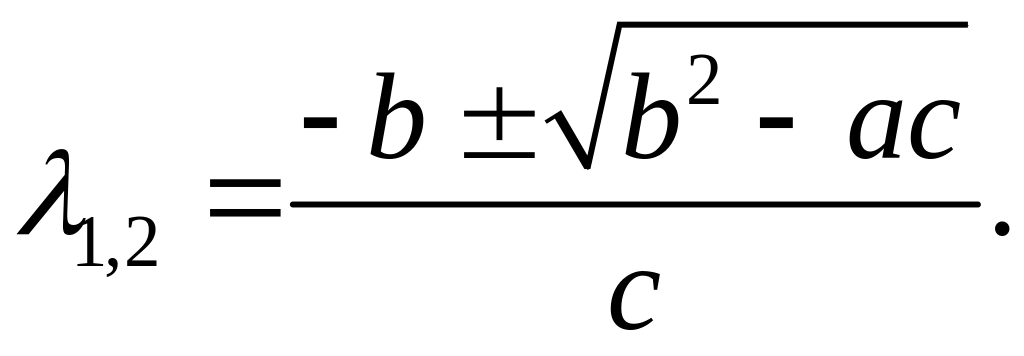В зависимости от значений дискриминанта возможны три случая:

1. D > 0 – уравнение гиперболического типа

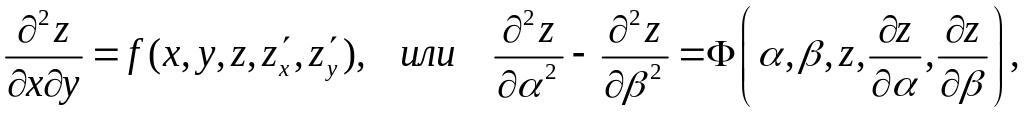
где

2. D = 0 – уравнение параболического типа

3. D < 0 – уравнение эллиптического типа

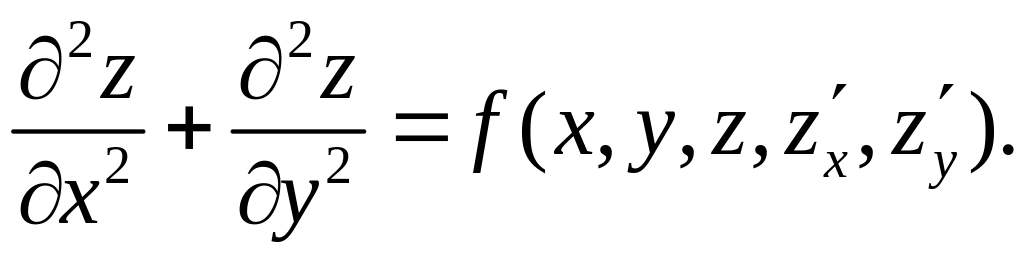
_{В общем случае вводятся новые переменные – дважды непрерывно дифференцируемые функции} и .

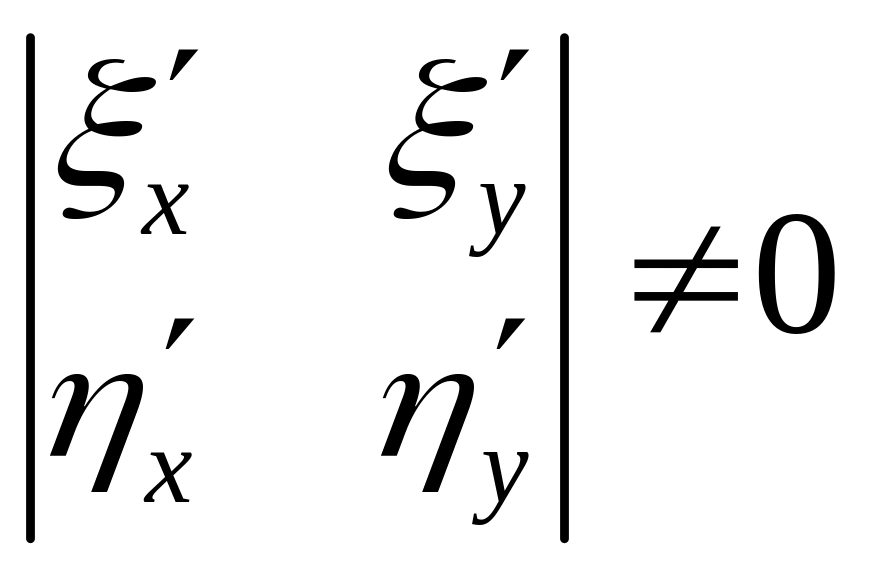Дифференциальное уравнение называется уравнением характеристик уравнения

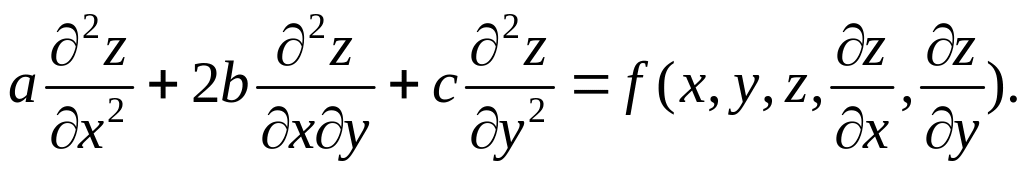
2.3. Волновые уравнения

В математической физике под струной понимают гибкую, упругую нить. Натяжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины в начальный момент направлена по отрезку оси от 0 до . Предположим, что концы струны закреплены в точках и . Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя положение, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.

Рассмотрим малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси OX и в одной плоскости (рис. 2.1). При этом предположении процесс колебания струны описывается одной функцией _{, которая дает величину перемещения} точек струны с абсциссой в момент .

Рис. 2.1. Малые отклонения струны в плоскости

_{Так как рассматриваются малые отклонения струны в плоскости , то будем предполагать, что длина элемента струны равняется ее проекции на ось , т.е. . Также предполагается, что натяжение Т во всех точках струны одинаковое. На концах этого элемента, по касательным к струне, действует сила} .

Касательные образуют с осью 0Х углы и . Тогда проекция на ось сил, действующих на элемент , будет равна Так как угол мал, можно положить , тогда имеем, что

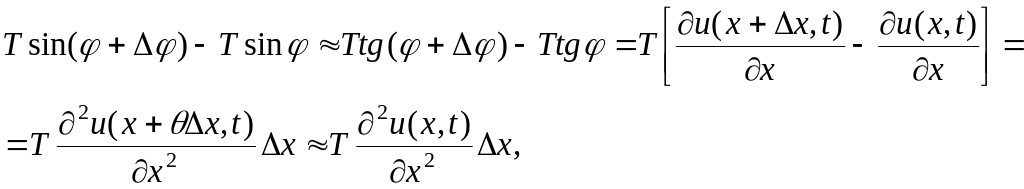
где 0 < θ < 1 – параметр согласно формуле приращений конечных разностей Лагранжа.

Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть ρ – линейная плотность струны. Тогда масса элемента струны будет . Ускорение элемента равно . Следовательно, по принципу Даламбера будем иметь . Сокращая на и обозначая 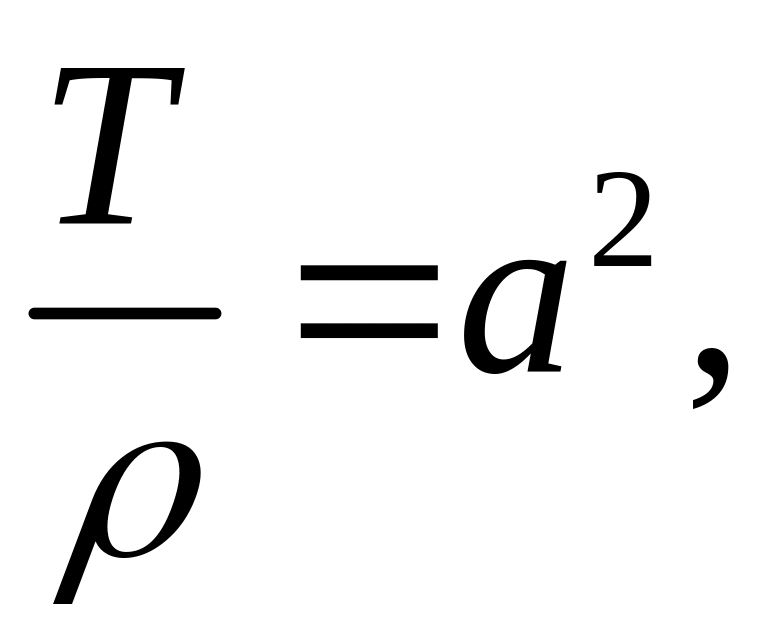получаем уравнение движения

. (2.7)

Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения _{движения струны одного уравнения (2.7) недостаточно. Искомая функция} должна удовлетворять еще граничным условиям, указывающим, что делается на концах струны ( и ), и начальным условиям, описывающим состояние струны в начальный момент ( ).