1.2. Вариационные принципы и математические модели

Дадим упрощенную формулировку вариационного принципа Гамильтона для механической системы. На его основе выведем уравнения движения шарика на пружине и маятника, в поле сил тяжести. Сопоставим результаты получения моделей из фундаментальных законов и из вариационного принципа.

Общая схема принципа Гамильтона. Пусть имеется механическая система, формального и строгого определения которой пока давать не будем, имея в виду, однако, что все взаимодействия между элементами такой системы определяются законами механики. Введем понятие обобщенных координат , полностью определяющих положение механической системы в пространстве. Величина может быть декартовой координатой (например, координата в системе «шарик пружина»), радиусом-вектором, «угловой координатой», набором координат материальных точек, составляющих систему, и т. д. Величину естественно назвать обобщенной скоростью механической системы в момент времени . Набор величин и определяет состояние механической системы во все моменты времени.

Для описания механической системы вводится функция Лагранжа, построение которой - отдельный вопрос, более подробно рассматриваемый.

В простейших случаях функция Лагранжа имеет ясный смысл и записывается в виде

где – кинетическая и потенциальная энергии системы соответственно. Для целей данного раздела нет необходимости давать общее определение величин , поскольку в рассматриваемых примерах они вычисляются очевидным образом.

Введем далее величину называемую действием:

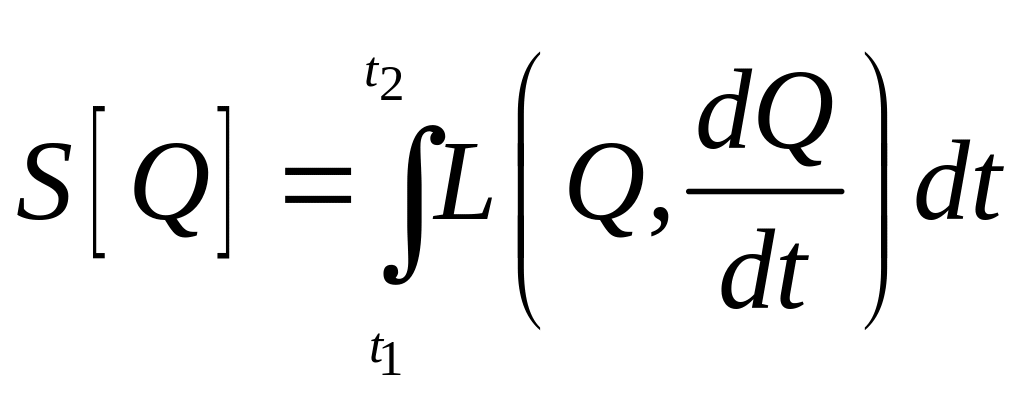. (1.7)

Интеграл, очевидно, является функционалом от обобщенной координаты функции , т.е. функции , заданной на отрезке он ставит в соответствие некоторое число S (действие).

Принцип Гамильтона для механической системы гласит: если система движется по законам механики, то – стационарная для функция или

. (1.8)

Фигурирующая в принципе наименьшего действия функция некоторая пробная функция, обращающаяся в нуль в моменты t₁, t₂ и удовлетворяющая тому условию, что – возможная координата данной системы (в остальном произвольна).

Смысл принципа в том, что из всех априори мыслимых (допускаемых) траекторий (движений) системы между моментами t₁, t₂ выбирается (реализуется) движение, доставляющее минимум функционалу действия (отсюда происходит и название принципа). Функция называется вариацией величины .

Итак, схема применения принципа Гамильтона для построения моделей механических систем состоит в следующем: определяются обобщенные координаты и обобщенные скорости системы, строятся функция Лагранжа и функционал действия минимизация которого на вариациях координаты и дает искомую модель.

Способ получения модели системы «шарик – пружина»

Воспользуемся принципом Гамильтона для построения модели движения шарика, соединенного с пружиной. В качестве обобщенной координаты системы естественно выбрать обычную эйлерову координату шарика r(t). Тогда обобщенная скорость – обычная скорость шарика. Функция Лагранжа, равная L = E_К – E_П, записывается через значения кинетической и потенциальной энергии системы:

(1.9)

Для величины действия получаем выражение

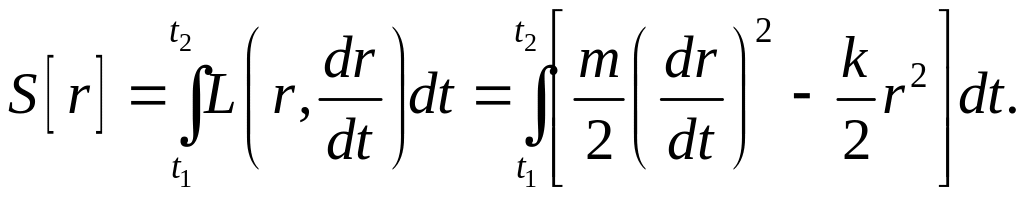(1.10)

Теперь в соответствии со схемой вычислим действие на вариациях координаты

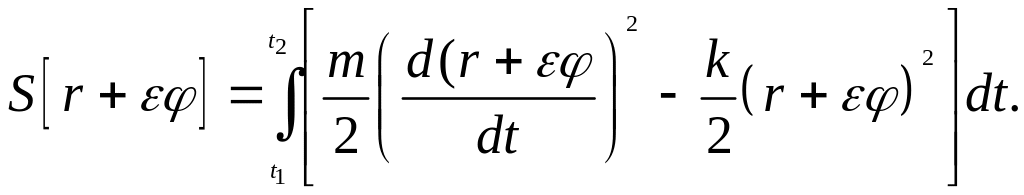(1.11)

Последнюю формулу необходимо продифференцировать по ε (учитывая, что функции от ε не зависят):

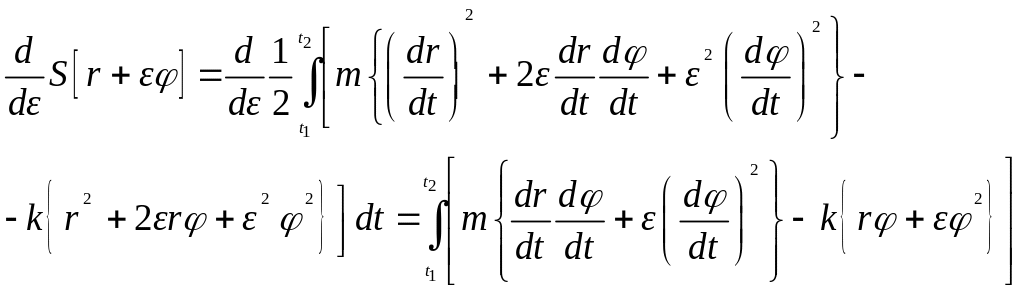
и положить в ней ;

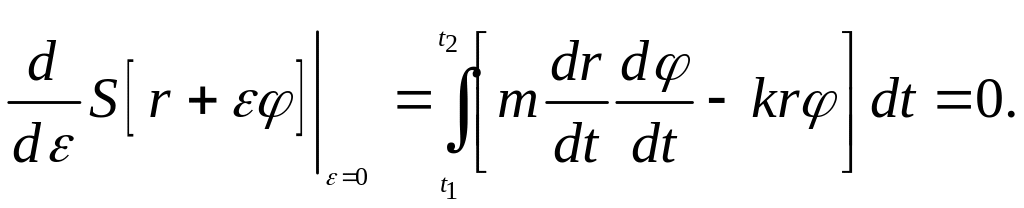(1.12)

Воспользовавшись формулой интегрирования по частям, последнее соотношение преобразуется к виду

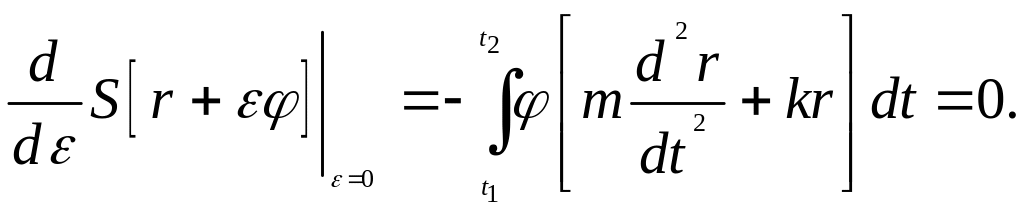(1.13)

Поскольку пробная функция , фигурирующая в формулировании принципа наименьшего действия, произвольна, то часть выражения, стоящая под знаком интеграла в квадратных скобках, должна быть равна нулю во все моменты времени t₁ < t < t₂:

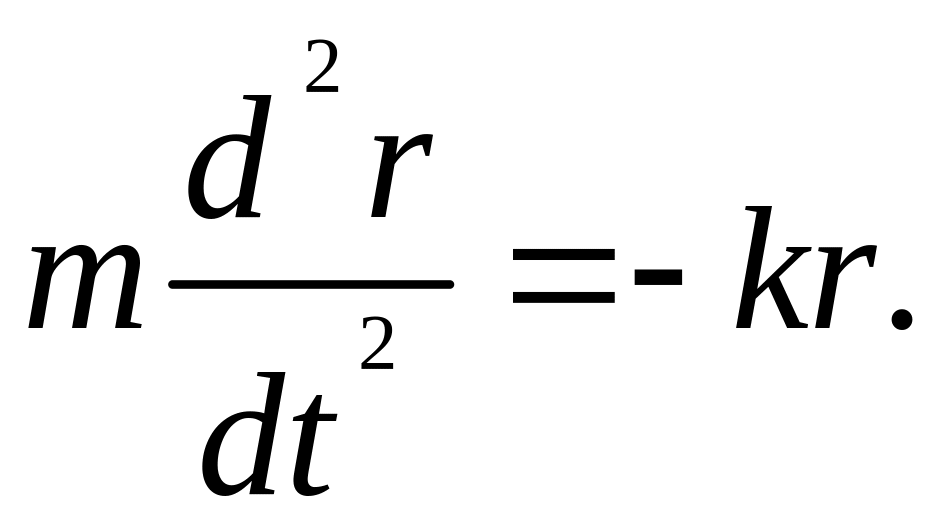(1.14)

Таким образом, полученное уравнение совпадает с уравнением (1.1).