6.2. Вывод уравнений Лоренца

Для вывода уравнений Лоренца в системе (6.6) исключим поле давлений, для чего продифференцируем первое уравнение по у, а второе – по x и вычтем одно из другого. В результате система уравнений принимает вид

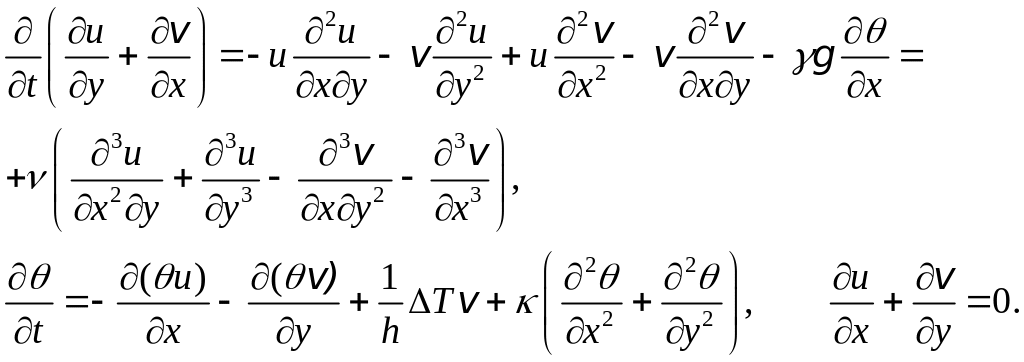(6.7)

Следующий шаг состоит в том, чтобы представить искомые поля в виде разложения в ряды по некоторой полной системе базисных функций; после этого предметом рассмотрения станет зависимость от времени коэффициентов разложения. Такой подход известен как метод Галеркина. Будем строить разложение по базису тригонометрических функций вида

(6.8)

где , m и n – целые.

На этом этапе желательно четко представлять себе конфигурацию течения, что позволит конкретизировать структуру разложения.

Примем как известный из эксперимента факт наличие режима конвекции в виде валов (рис. 6.2).

Рис. 6.2. К выбору структуры разложения решения в

ряд по базисным функциям

Взяв одну ячейку, расположенную в области 0 < х < 1, 0 < у < Н, можно считать течение периодически продолженным, как на рис. 6. 2. В таком течении температура должна быть четной функцией х и нечетной функцией у, т. е. мы должны положить

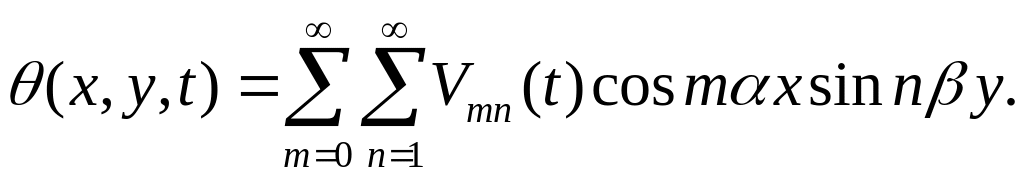(6.9)

Чтобы записать соотношение для компонент скорости, полезно заметить, что из условия нулевой дивергенции следует, что и и v должны выражаться через производные от одной и той же функции ψ(х, у, t), называемой функцией тока: , . Как видно из рис. 6.2, компонента и должна быть нечетной по x и четной по у, а компонента v, наоборот, четной по х и нечетной по у. Эти условия будут выполнены, если функцию тока представить в виде

(6.10)

тогда для компонент скорости имеем

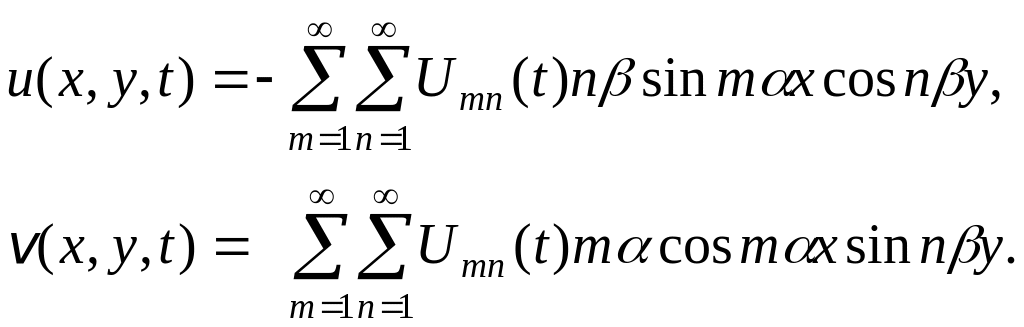(6.11)

Далее можно подставить выражения (6.9) и (6.11) в уравнения (6.7) и, используя соотношения ортогональности для базисных функций, получить систему уравнений (бесконечную) для коэффициентов U_тп и V_тп. Работать с бесконечной системой трудно, если вообще возможно, поэтому ряды нужно каким-то разумным способом обрезать. Модель Лоренца получается, если считать существенными и отличными от нуля члены U₁₁, V₁₁, V_02. Эти амплитуды обозначим через X, Y и Z соответственно. Итак, полагаем

(6.12)

Подставим эти выражения в первое уравнение (6.7). В полученном соотношении все возникающие комбинации синусов и косинусов нужно привести с помощью тригонометрических формул к суммам членов вида (6.8), а затем отбросить члены, отличные по структуре от единственной присутствующей в левой части комбинации вида Приравнивая коэффициенты в левой и правой части, получаем

. (6.13)

Со вторым уравнением поступаем аналогично. Разница, однако, в том, что в левой части теперь присутствуют две пространственные моды – комбинации вида и Приравнивая коэффициенты перед членами такого вида в левой и правой частях, получаем два уравнения:

, (6.14)

. (6.15)

Итак, мы нашли систему трех обыкновенных дифференциальных уравнений для динамических переменных X, Y, Z. Чтобы с ней было удобно работать, полезно привести уравнения к безразмерному виду посредством некоторой замены переменных и параметров. Подставим в (6.13) – (6.15) X=Аx, Y = By, Z = Cz, t = Dτ, где A, B, C, D – некоторые постоянные коэффициенты. Тогда получаем

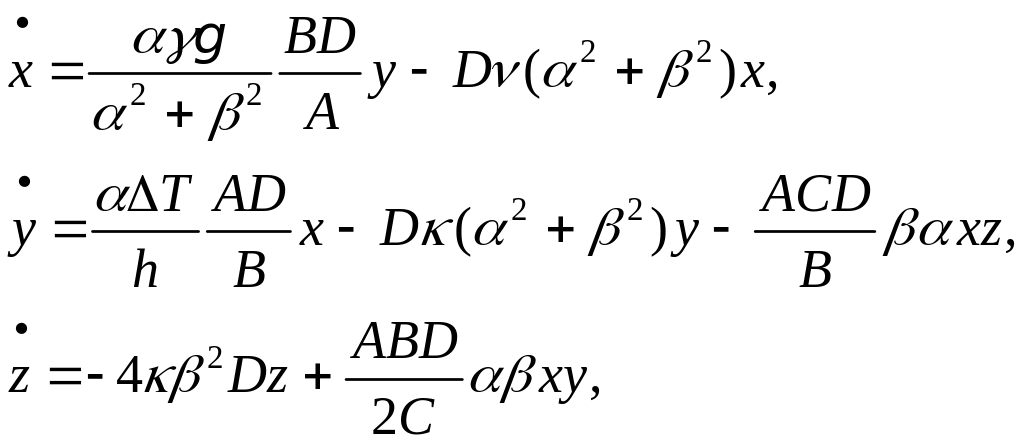(6.16)

где точка означает теперь производную по τ. Попробуем подобрать коэффициенты так, чтобы вид уравнений максимально упростился. Положим

(6.17)

Отсюда можно найти

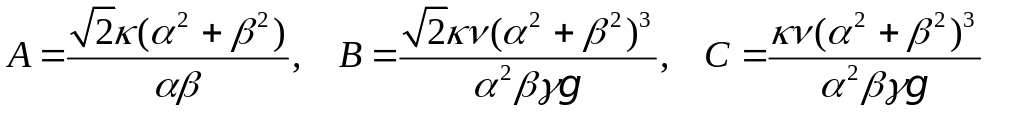. (6.18)

Кроме того, введем безразмерные параметры

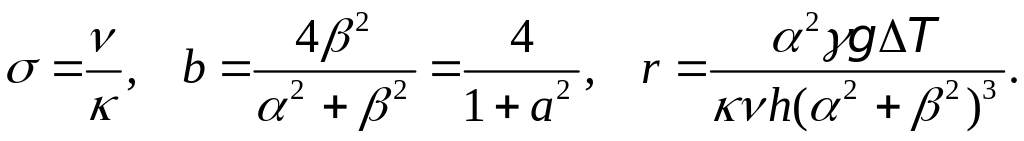(6.19)

Тогда уравнения (6.16) принимают вид

. (6.20)

Это и есть модель Лоренца. Она представляет собой динамическую систему с трехмерным фазовым пространством. Мгновенное состояние определяется набором трех переменных (x, у, z), а оператор эволюции определен конкретным видом уравнений (6.20). (Согласно теореме существования и единственности решения системы дифференциальных уравнений, если задано начальное состояние (x, у, z), то однозначно определено и состояние в любой последующий момент.)

Физический смысл переменных, фигурирующих в уравнениях Лоренца, можно проинтерпретировать на основании соотношений (6.9) и (6.11). Переменная x характеризует скорость вращения конвекционных валов, величины у и z отвечают за распределение температуры соответственно по горизонтали и по вертикали. Параметр b определяется геометрией конвекционной ячейки, а именно, отношением ее вертикального и горизонтального размеров а. Параметр есть отношение коэффициента кинематической вязкости и коэффициента температуропроводности . Его называют числом Прандтля. Комбинацию 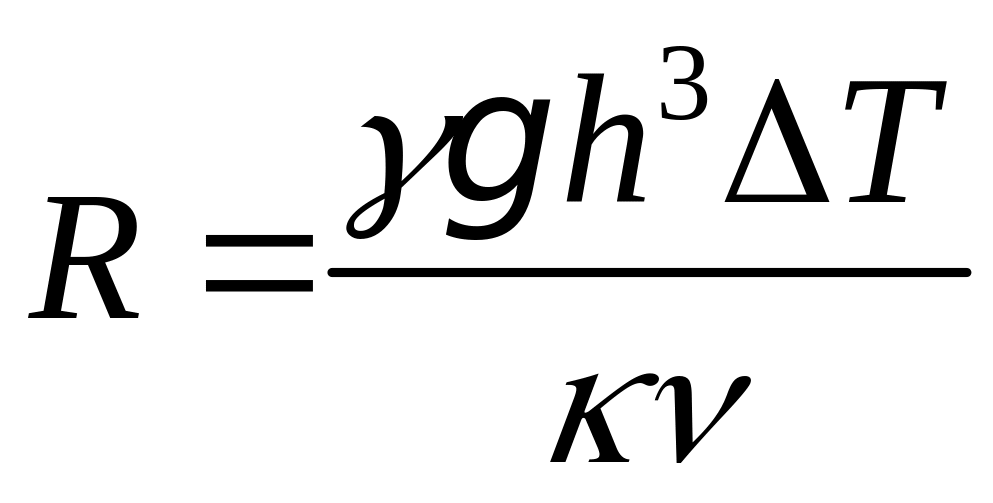называют числом Рэлея. В свое время Рэлей показал, что условию возникновения конвекционного течения в виде валов отвечает определенное критическое значение этого числа, а именно, . Из формулы (6.19) видно, что параметр r представляет собой отношение R/R_с.