Контрольные вопросы и задания

3.2. Определить тип и найти общее решение уравнений:

а) ; б) ; в) .

3.3. Найти общее решение уравнения: .

3.4. Используя замены , упростить следующие уравнения (привести к каноническому виду):

а) ;

б) ;

в) .

3.5. Найти общее решение уравнения: .

Указание. Перейти к характеристическим переменным .

3.6. Используя формулу Даламбера, найти решение уравнений:

а) ;

б) ;

в) ;

г) ;

д) .

3.7. Найти в области решение уравнения ,

удовлетворяющее однородным краевым условиям:

и следующим начальным условиям:

а) ; б) ;

в) ;

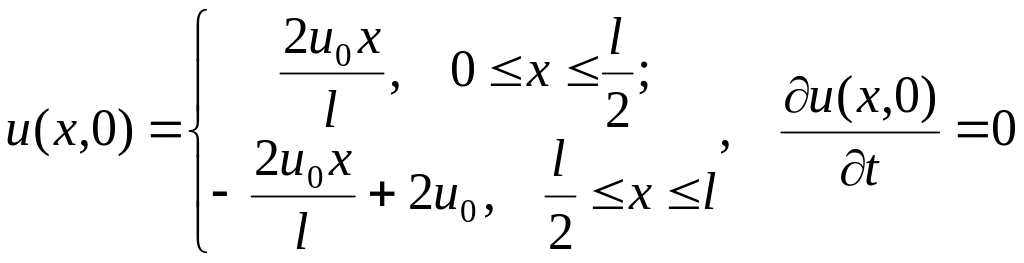г) .

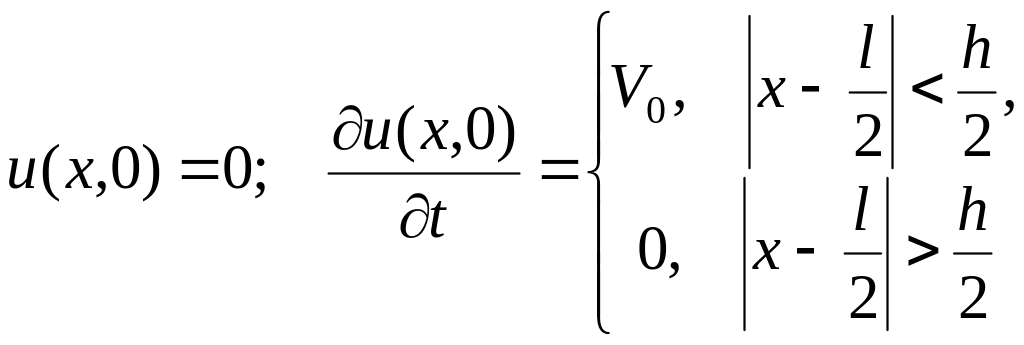3.8. Найти решение уравнения в области , удовлетворяющее краевому условию и начальным условиям:

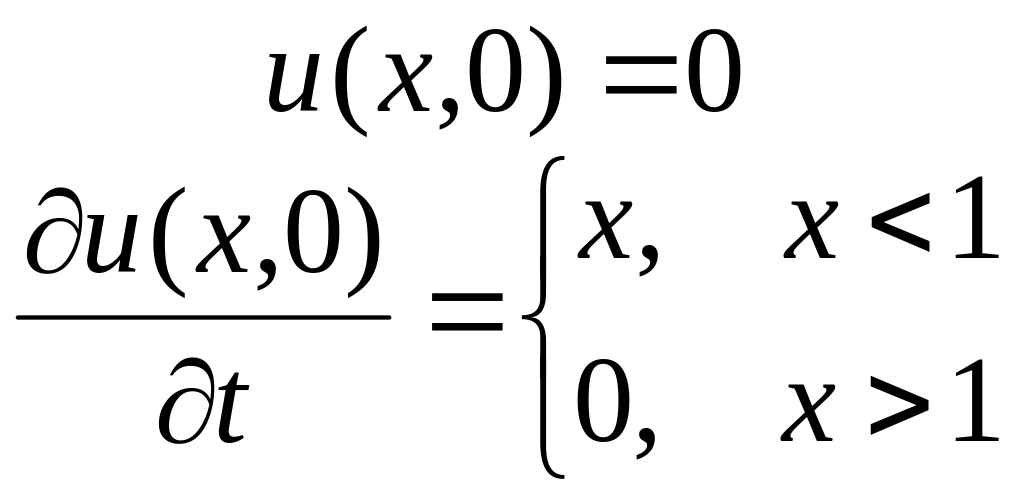
Указание. Использовать преобразование Фурье (косинус или синус).

4. Уравнение теплопроводности

4.1. Вывод уравнения теплопроводности. Первая краевая задача

Рассмотрим однородный теплоизолированный с боков стержень конечной длины , имеющий постоянную по длине толщину, и настолько тонкий, чтобы в любой момент времени температуру тела во всех точках поперечного сечения можно было бы считать одинаковой.

Выберем ось (направив ее по оси стержня) так, чтобы стержень совпадал с отрезком [0; ] оси (рис. 4.1).

Рис.4.1. Однородный теплоизолированный с боков стержень

Обозначим температуру стержня в сечении x в момент t через . Тогда функция задает закон распределения температуры в стержне. Выведем дифференциальное уравнение для этой функции.

Выделим элемент стержня [x, x+Δx] и составим для него уравнение теплового баланса, согласно которому скорость изменения количества тепла в рассматриваемом объеме (изменение количества тепла в единицу времени), обусловленная теплоемкостью материала, равна количеству тепла, поступившему в этот объем в единицу времени вследствие теплопроводности.

_{Скорость изменения тепла в выделенном элементе стержня равна}

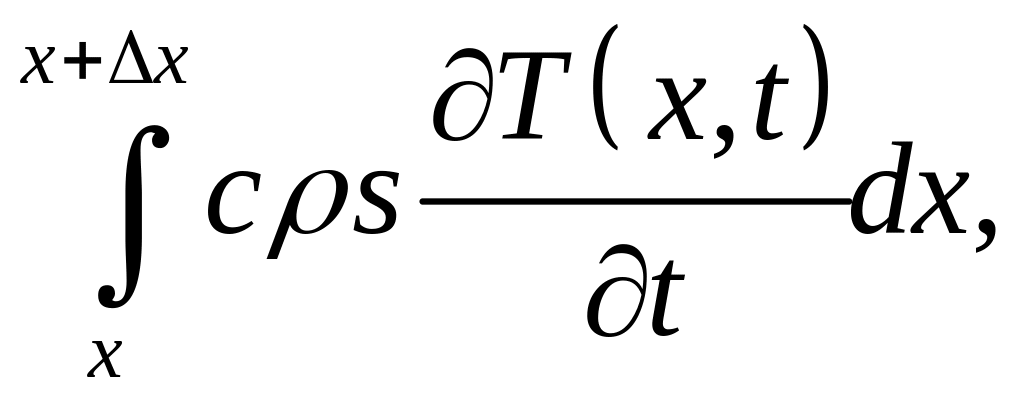
где с – теплоемкость материала стержня, ρ – плотность, s – площадь поперечного сечения стержня.

По теореме о среднем

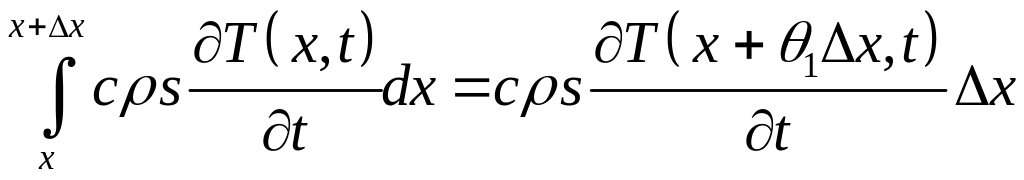, где 0 < θ₁ < 1.

Найдем количество тепла, поступившее в выделенный элемент стержня за единицу времени. Так как стержень теплоизолирован с боков, то тепло может поступать только через сечения, ограничивающие выделенный элемент стержня. Известно, что количество тепла, протекающее через сечение с абсциссой x за единицу времени, равно 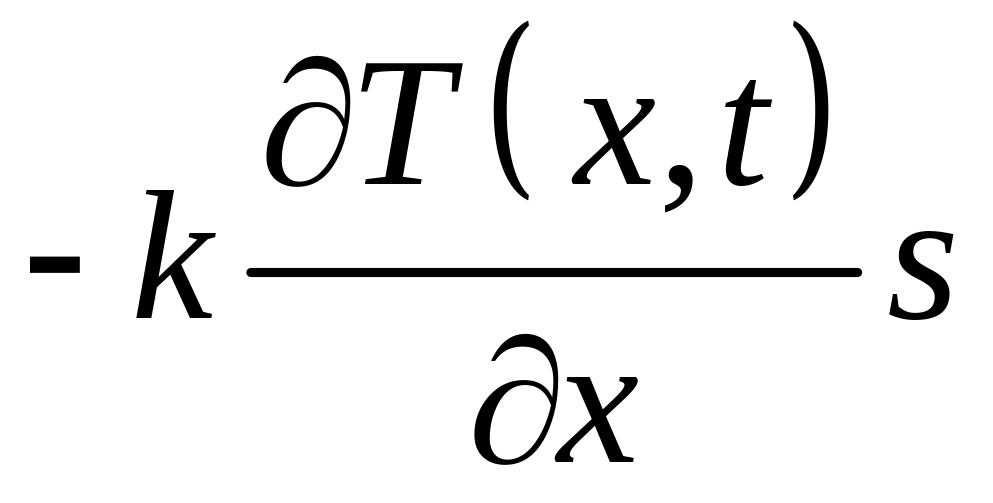, где k – коэффициент теплопроводности, s – площадь сечения.

Поэтому искомое количество тепла равно

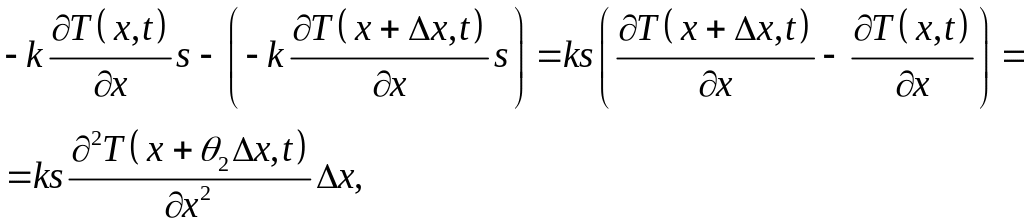
где 0 < θ₂ < 1. (Согласно формуле конечных приращений Лагранжа к функции

).

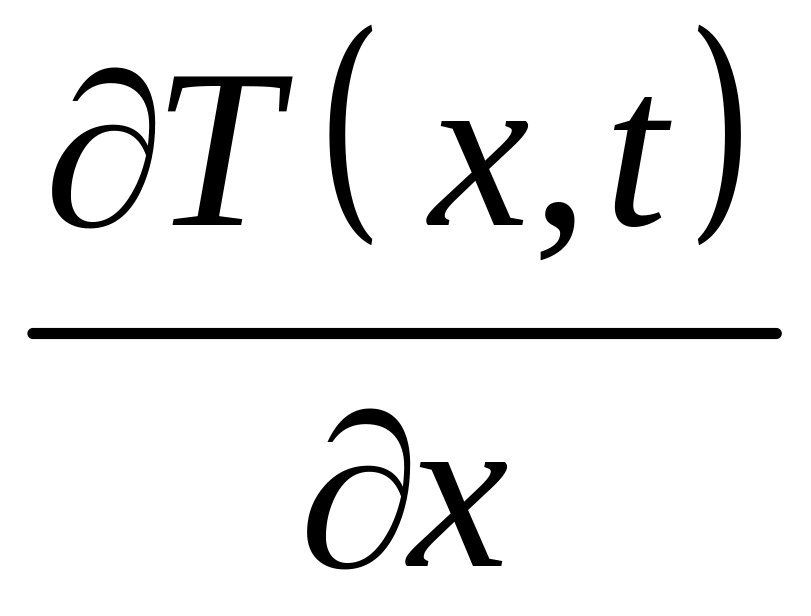Тогда уравнение теплового баланса будет иметь вид

.

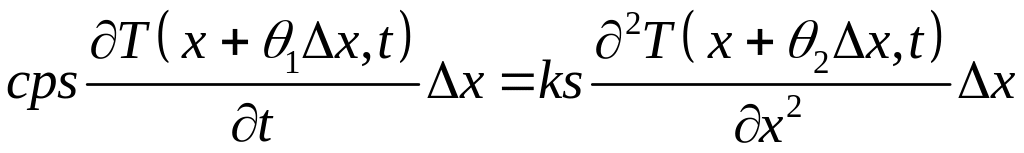Разделим обе части этого уравнения на sΔx (объем выделенного элемента стержня) и устремим Δx к нулю (стягивая выделенный элемент стержня к сечению). Получим уравнение теплопроводности для однородного стержня

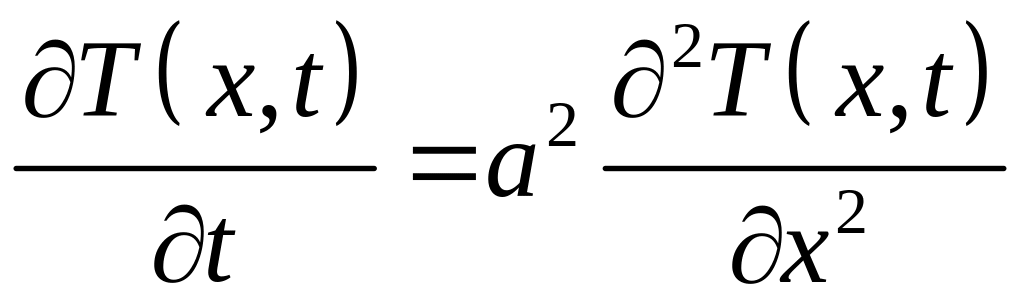, (4.1)

где 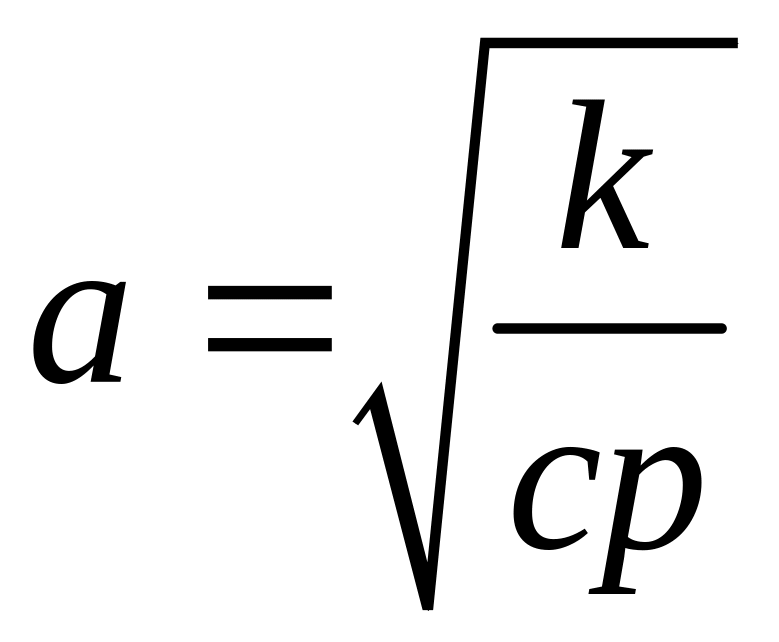– коэффициент температуропроводности.

Искомая функция должна удовлетворять уравнению (4.1), начальному условию , где – заданная функция от координат (это условие выражает закон распределения температуры по длине стержня в начальный момент времени) и граничным условиям

,

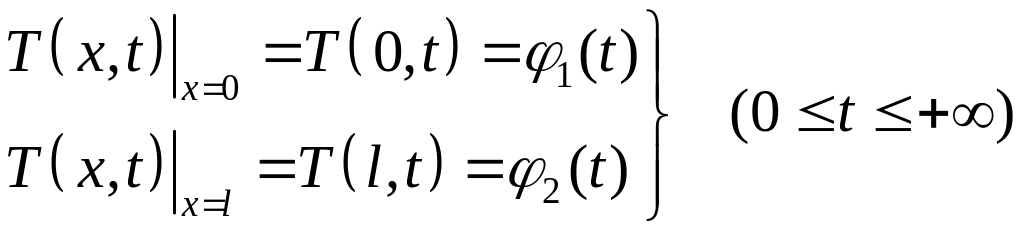где и – заданные функции от времени. Они определяют температуру, поддерживаемую на конце стержня. Данное уравнение не учитывает тепловой обмен между поверхностью стержня и окружающим пространством.

Рассмотрим первую краевую задачу для уравнения теплопроводности. Пусть Ω – конечная область трехмерного пространства, S – граница области Ω, Q –цилиндр с основанием Ω в пространстве переменных (x, y, z, t), образующие которого параллельны оси 0t. Q_Т – часть этого цилиндра, ограниченная плоскостями t = 0 и t = Т (Т > 0), часть границы цилиндра Q_Т , состоящую из его нижнего основания и боковой поверхности, обозначим через Г.

Найдем в цилиндре Q_Т решение уравнения теплопроводности

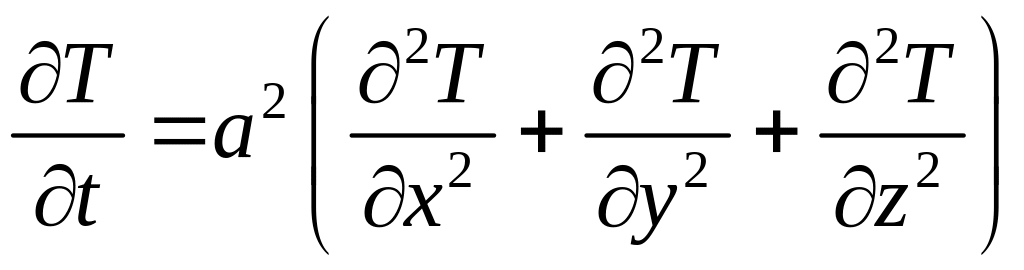, (4.2)

удовлетворяющее начальному условию

(4.3)

и граничному условию

, (4.4)

где Р – точка поверхности S. Функции и непрерывны, причем значения при t = 0 совпадают со значениями на границе S.

Задача нахождения решения уравнения (4.2) при условиях (4.3), (4.4) называется первой краевой задачей для уравнения теплопроводности.

Теорема. Функция , удовлетворяющая однородному уравнению теплопроводности (4.2) внутри цилиндра Q_Т и непрерывная вплоть до его границы, принимает наибольшее и наименьшее значение на Г, т. е. или при t = 0, или на боковой поверхности цилиндра Q_Т.

Из этой теоремы непосредственно вытекает, что:

1. решение первой краевой задачи единственно;

2. решение первой краевой задачи непрерывно зависит от правых частей начального и граничных условий;

3. если функция Т, непрерывная на замыкании Q_Т и удовлетворяющая первой краевой задаче, равна нулю на Г, то она тождественно равна нулю в замыкании Q_Т.