§6. Основы дифференциального метода прогнозирования опасных факторов пожара, численная реализация дифференциальной математической модели

Наиболее детальный уровень моделирования могут обеспечить, в принципе полевые модели пожара [4]. Эти модели называют дифференциальными. Полевые модели базируются на использовании дифференциальных уравнений в частных производных, описывающих пространственно-временное распределение температур и скоростей газовой среды в помещении, концентраций компонентов газовой среды (кислорода, продуктов горения и т.д.), давлений и плотностей. Эти уравнения включают реологический закон Стокса, закон теплопроводности Фурье, законы диффузии, законы радиационного переноса и т.п. Система уравнений, описывающих изменения во времени указанных параметров газовой среды в каждой точке пространства внутри помещения чрезвычайно громоздка. Решение названной системы осуществляется с помощью ЭВМ. Результаты решения получаются в форме полей скоростей, температур, концентраций продуктов горения и кислорода в любой момент времени протекания пожара.

Реализация полевых моделей ограничена уровнем современных знаний о таких, например, явлениях, как турбулентность и радиационно-конвективный тепломассоперенос в поглощающей и рассеивающей среде, каковой является задымленный газ в помещении при пожаре. По этой причине разработанные к настоящему времени полевые модели носят ограниченный характер.

В настоящем курсе лекций рассматриваются две простейшие полевые модели. В первой модели принимается самая простая гипотеза относительно турбулентных процессов переноса в газовой среде, заполняющей помещение, и считается возможным ограничиться рассмотрением переноса энергии в газовой среде только путем конвекции и теплопроводности. (Эта модель была разработана в 1987 г. И.Ф. Астаховой.) Кроме того, газовая среда в помещении как вязкая теплопроводная несжимаемая жидкость в приближении Буссинеска (сжимаемость учитывается в члене с архимедовой силой). Уравнение энергии в силу вышесказанного не содержит член, описывающий радиационный перенос энергии. Предполагается, что поля всех параметров являются двумерными (а не трехмерными, как это имеет место в большинстве реальных случаев), т.е. пространственная постановка задачи заменяется плоской; коэффициенты турбулентного переноса (турбулентная вязкость и теплопроводность) принимаются постоянными величинами для всех точек пространства внутри помещения; расчет температурных полей в ограждающих конструкциях основан на использовании дифференциального уравнения Фурье-Кирхгофа, записанного в линейном приближении. В качестве связи задач о поле температур в газовой среде и в ограждениях использовались эмпирические формулы, описывающие зависимость коэффициентов теплоотдачи на поверхностях ограждений от температур газовой среды и поверхности ограждений.

Эта модель представлена следующими уравнениями для газовой среды в помещении:

, (6.1)

, (6.2)

, (6.3)

, (6.4)

где - число Грасгофа; - - число Прандтля; - число Рейнольдса; , - безразмерные составляющие скоростей , - безразмерные координаты; - безразмерное время; - характерная скорость; g - ускорение свободного падения; Н - высота помещения; L - размер помещения вдоль оси x; ν -коэффициент эффективной (турбулентной) вязкости; а – эффективная температуропроводность; - безразмерное давление; Δр – перепад давлений; Q₁ - мощность источника горения в безразмерном виде; Θ -безразмерный перепад температур.

В качестве значений Θ на ограждающих конструкциях берется решение следующей задачи о нагревании ограждения:

, (6.5)

, (6.6)

, (6.7)

, (6.8)

, (6.9)

где Т - температура ограждения; b - толщина ограждающей конструкции; а₁ - коэффициент температуропроводности материала ограждения; Θ_р -температура набегающего газа; α - коэффициент теплообмена на необогреваемой поверхности конструкции; λ - коэффициент теплопроводности материала ограждающей конструкции; α₁ - коэффициент теплоотдачи на обогреваемой поверхности конструкции, который вычисляется по эмпирическим формулам; q - эффективное падающее излучение; Т_Н - температура воздуха с необогреваемой стороны.

В этой модели не рассматривается задымление и состав среды в помещении. Поэтому математическая модель не содержит уравнений диффузии. Для численного решения с помощью ЭВМ математической модели предлагается использовать один из методов дробных шагов - метод Писмена-Рекфорда.

Характеризуя в целом эту полевую модель, необходимо сделать ряд замечаний. Прежде всего, следует отметить, что уравнения энергии (6.1) и движения (6.2), (6.3) нужно рассматривать как результат усреднения по методу Рейнольдса актуальных уравнений и поэтому коэффициенты переноса (вязкость и теплопроводность) в этих уравнениях зависят от характера гидродинамических и термодинамических процессов в движущейся среде. Значения этих коэффициентов могут существенно различаться в разных точках помещения. Проблема вычисления этих коэффициентов есть центральная проблема турбулентности в гидродинамике.

В модели И.Ф. Астаховой принимается, что значения коэффициентов турбулентной вязкости и теплопроводности есть постоянные величины, не зависящие ни от координат, ни от времени. При этом следует сказать, что заранее не известно, какие конкретные числовые значения этих коэффициентов нужно брать. Из общих соображений и качественных оценок известно, что турбулентные коэффициенты переноса в тысячи и десятки тысяч раз больше своих "ламинарных" (молекулярных) аналогов. Подобрать "приемлемые" значения этих коэффициентов можно лишь путем сравнения данных расчета с данными физического эксперимента. Есть основания предполагать, что числовые значения этих коэффициентов, помимо всего прочего, могут зависеть от геометрических размеров пожара (масштабный фактор). Это обстоятельство и двухмерность рассмотренной полевой модели ограничивают сферу ее практического использования.

Вторая модель, которую мы рассмотрим, базируется на следующих допущениях: газовая среда в помещении так же, как в первой модели, рассматривается как несжимаемая жидкость в приближении Буссинеска, эффекты излучения в работе также не рассматриваются. В первом варианте модели предполагается, что температура ограждающих поверхностей есть постоянная величина ("изотермические" граничные условия), а во втором варианте предполагается равенство нулю градиентов температур в газовой среде около поверхности ограждении ("адиабатные" граничные условия). В отличие от первой модели проблема турбулентности решалась путем использования гипотезы о вихревой вязкости. При моделировании горения используется допущение о существовании локального термодинамического и химического равновесия (диффузионная модель горения).

Система уравнений, моделирующая пожар, представлена в переменных "функция тока" - "вихрь" ( ). Она включает уравнения сохранения завихренности , уравнение для определения функции тока , уравнения сохранения энергии потока φ₀ и концентрации нейтрального компонента :

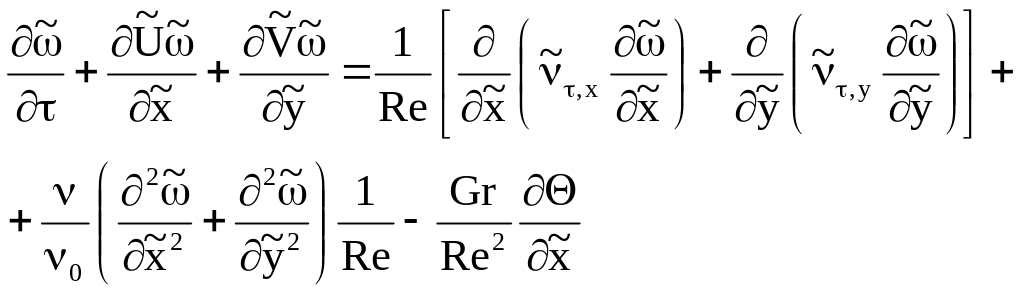, (6.10)

. (6.11)

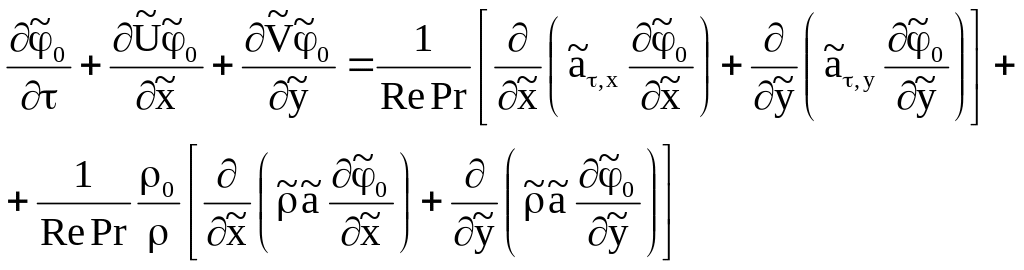, (6.12)

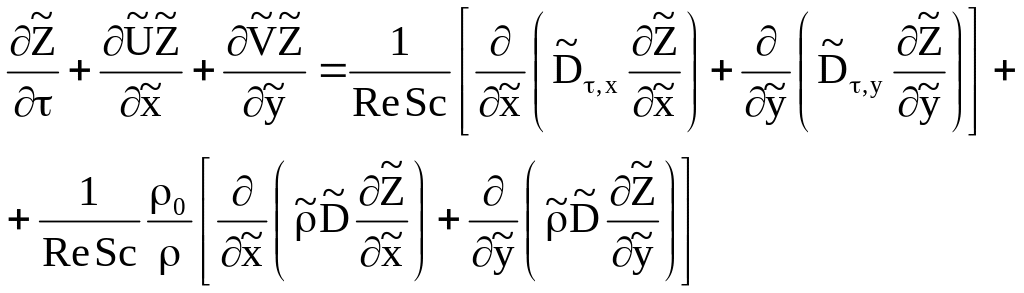, (6.13)

где ω - завихренность, с^-1; ψ - функция тока, м²/с; - безразмерная энергия потока; - безразмерная энтальпия; h_S, h₂ - значения энтальпии в пламени и в потоке воздуха; Re, Gr, Pr, Sc, Pr_τ, Sc_τ -соответственно числа Рейнольдса и Грасгофа, а также числа Прандтля и Шмидта для ламинарного и турбулентного режимов течения; l, l_max - текущая и максимальная длина пути смешения, м; n- нормаль к ограждающим поверхностям помещения м; Н - высота помещения, м; - масштаб скорости, м/с; ρ₀ - плотность окружающей среды, кг/м³; ν_τ,x, ν_τ,y, a_τ,y - коэффициенты турбулентного обмена вдоль осей х, у, м²/с.

Для численной реализации нестационарные уравнения завихренности, энергии и концентрации компонента Z записывались в общем виде в консервативной форме. В целях более точной аппроксимации основных уравнений и учета приграничных эффектов для решений этих уравнений применялась консервативная конечно-разностная схема второго порядка точности по пространственной переменной и первого порядка по временной переменной. Решение нестационарных уравнений производилось по явной двухслойной схеме на пятиточечном шаблоне типа "крест". Для конвективных членов па n-м временном слое использована односторонняя аппроксимация, учитывающая направление потока в ячейке. Уравнение Пуассона для функции тока решалось методом итерации с применением верхней релаксации. Для аппроксимации граничных условий использованы конечно-разностные соотношения первого и второго порядка точности. При решении конечно-разностных уравнений созданы алгоритм и программа для реализации модели пожара в помещении с помощью ЭВМ.

В связи с тем, что теория процессов переноса в движущейся среде при пожаре в помещении в настоящее время разработана еще не полностью, нельзя ожидать достоверных количественных результатов при использовании дифференциальных моделей пожара. Тем не менее, эти модели позволяют получать хорошие в качественном отношении представления о картине вихревого движения газа и о распределении температур в среде при пожаре в помещении.

В приказе Министерства РФ по делам гражданской обороны, чрезвычайным ситуациям и ликвидации последствий стихийных бедствий от 30июня 2009 г. № 382 "Об утверждении методики определения расчетных величин пожарного риска в зданиях, сооружениях и строениях различных классов функциональной пожарной опасности" [6] в приложении № 6 изложен порядок проведения расчета и математические модели для определения времени блокирования путей эвакуации опасными факторами пожара, который приведен в приложении настоящего курса лекций.

Контрольные вопросы.

Расскажите про дифференциальные (полевые) математические модели пожара в помещении.