ФГБОУ ВО

«Воронежский государственный технический университет»

Кафедра физики

Энтропия. Теоретические и практические материалы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по физике

для студентов всех технических направлений

и специальностей очной формы обучения

Воронеж 2016

Составитель канд. физ.-мат. наук Н.В. Агапитова

УДК 681.3; 53

Энтропия. Теоретические и практические материалы: методические указания по физике для студентов всех технических направлений и специальностей очной формы обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост. Н.В. Агапитова. Воронеж, 2016. 43 c.

Методические указания содержат теоретическую и практическую разработку темы «Энтропия» в курсе физики: рассмотрены вопросы теории этой сложной для восприятия темы, приведен обстоятельный подбор примеров решения задач и список задач для самостоятельного решения.

Методические указания предназначены для студентов первого курса очной формы обучения.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле Энтропия.doc.

Ил. 13. Библиогр.: 10 назв.

Рецензент д-р физ.-мат. наук, проф. А.В. Бугаков

Ответственный за выпуск зав. кафедрой канд. физ.-мат. наук, проф. Т.Л. Тураева

Издается по решению редакционно-издательского совета Воронежского государственного технического университета.

 ФГБОУ ВО «Воронежский государственный

технический университет», 2016

Предисловие

Методические указания представляют собой теоретические и практические материалы по достаточно сложной для восприятия теме курса общей физики «Энтропия».

Методические указания содержат всестороннюю разработку данной темы.

В лаконичной форме и в тоже время на достаточном научно-методическом уровне рассмотрены сложные вопросы введения функции состояния «энтропии», ее свойства, связь энтропии с термодинамической вероятностью состояния системы.

Наряду с этим обстоятельно представлены примеры решения задач на расчет энтропии.

Кроме того, в методических указаниях предложен подробный подбор задач для самостоятельного решения студентами. Задачи квалифицированы по уровню сложности на три типа: базовый – А, повышенный – В и высокий – С.

Данные методические указания могут быть с успехом использованы студентами, проработка этих материалов будет способствовать успешному усвоению студентами данных тем учебной программы курса физики.

Наличие подробных методических указаний по данной теме поможет студентам в индивидуальной работе над усвоением материала, сделает ее комфортнее и результативнее.

1. Теоретическая часть

1.1. Приведённое количество тепла.

Неравенство Клаузиуса

Рассмотрим необратимый цикл Карно, проводимый в прямом направлении, т. е. действующий как тепловая машина. Согласно первой теоремы Карно

_{необратимого цикла Карно} _{обратимого цикла Карно}

Или учитывая, что коэффициент полезного действия всех обратимых машин, действующих между одними и теми же нагревателями и холодильниками, одинаков, а КПД необратимой машины всегда меньше, чем обратимой, можно записать

(1.1)

Знак равенства соответствует обратимой, а знак неравенства – необратимой машине.

Преобразуем (1.1):

, или , или

Вычтя из правой и левой части неравенства выражение , получим:

(1.2)

В соотношение (1.2) входит как тепло Q₁, получаемое системой, так и тепло , отдаваемое ею. Видоизменим это уравнение так, чтобы оно содержало только количество теплоты, получаемое системой от других тел; причём, эти теплоты будем рассматривать как величины алгебраические: получаемое тепло будет положительным, если оно передаётся от какого-то внешнего тела к системе, и – отрицательным, если оно отдается системой внешнему телу. Итак, вместо отдаваемого телу с температурой T₂ тепла введём получаемые от этого тела тепло . C учётом этого соглашения неравенство (1.2) преобразуется к виду

. (1.3)

Это соотношение называется неравенством Клаузиуса.

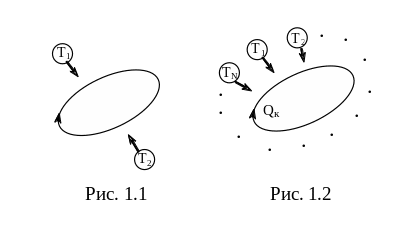
Отношение количества тепла, полученного системой от какого-либо тела, к температуре этого тела Клаузиус назвал приведённым количеством тепла. Используя терминологию Клаузиуса¹, неравенство (1.3) можно формулировать следующим образом: если какая-то система совершает цикл, в ходе которого вступает в теплообмен с двумя тепловыми резервуарами, температуры которых постоянны (рис. 1.1), то сумма приведённых количеств тепла равно нулю, если цикл обратим, и меньше нуля, если цикл необратим.

Если система в ходе цикла вступает в теплообмен не с двумя, а с N телами (рис. 1.2), причём от тела с температурой T_i получает количество тепла Q_i (которое может быть как положительным, так и отрицательным), естественно предположить по аналогии с (1.3), что должно выполняться следующее условие:

(1.4)

Чтобы не повторяться, условимся о том, что в дальнейшем во всех случаях, когда в каком-либо выражении будет стоять знак « » или « », то знак равенства будет относиться к обратимым про­цессам, а знак неравенства — к необратимым процессам. То же самое справедливо и для выражения (1.3).

До сих пор мы полагали, что теплоемкость тел, обменивающихся теплом с рассматриваемой системой, настолько велика, что процесс теплообмена не отражается на температуре T_i - этих тел. Если это условие не выполняется, то при передаче системе тепла Q_i - темпера­тура соответствующего тела T_i будет непрерывно меняться. Чтобы написать для этого случая выражение, аналогичное (1.3), нужно каждый из процессов передачи Q_i разбить на ряд элементарных про­цессов, настолько малых, чтобы передачу в ходе каждого из них элементарного количества тепла 'Q_i,- можно было считать происхо­дящей при постоянной (но своей для каждого 'Q_i) температуре Т_i. Тогда вместо (1.3) мы должны написать:

(1.5)

где индекс i означает уже не номер тела, с которым система вступает в теплообмен, а номер одного из элементарных процессов, на которые мы разбили цикл, совершаемый системой. 'Q_i означает количество тепла, получаемое системой в ходе i-го элементарного процесса от одного из внешних тел, T_i — температура этого внешнего тела в момент передачи им системе тепла 'Q_i. Значок О под зна­ком указывает на то, что сумма должна быть взята по всему

циклу.

Выражение (1.5) означает, что сумма элементарных приведенных . количеств тепла, получаемых системой в ходе цикла извне, равна нулю, если цикл обратим, и меньше нуля, если цикл необратим.

Строго говоря, (1.5) должно быть записано следующим образом:

, (1.6)

где интеграл берётся по всему циклу.

Рассуждения, приведшие нас от (1.5) к (1.6), отнюдь не могут рассматриваться как строгое доказательство. Однако выражение (1.6) может быть получено из (1.5) вполне строго.