
- •Часть 2
- •Часть 2
- •Введение
- •1. Элементы комбинаторики
- •1.1. Простейшие комбинаторные конфигурации
- •Основные правила комбинаторики
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Латинские прямоугольники, конечные проективные плоскости и блок-схемы
- •1.2.1. Латинские прямоугольники
- •1.2.2. Конечные проективные плоскости
- •1.2.3. Блок-схемы
- •Формула включений и исключений
- •Объединение комбинаторных конфигураций
- •1.3.2. Принцип включения и исключения
- •1.3.3. Число булевых функций, существенно зависящих от всех своих переменных
- •1.3.4. Решето Эратосфена
- •Рекуррентные уравнения
- •1.4.1. Определение рекуррентного уравнения
- •1.4.2. Решение линейного однородного рекуррентного уравнения
- •1 (2) .4.3. Решение линейного неоднородного рекуррентного уравнения
- •1.5. Производящие функции
- •1.5.1. Общие сведения о производящих функциях
- •1.5.2. Производящая функция для биноминальных коэффициентов
- •1.5.3. Производящая функция для чисел Фибоначчи
- •1.6.1. Определение z – преобразования
- •1.6.2. Обратное z – преобразование
- •В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.
- •1.6.3. Свойства z-преобразования
- •1.6.4. Использование z-преобразований для решения рекуррентных уравнений
- •1.6.5. Таблица односторонних z-преобразований
- •1.7. Трансверсали и перманенты
- •1.7.1. Множества и мультимножества
- •1.7.2. Трансверсали
- •1.7.3. Пермамент матрицы
- •1.7.4. Число трансверсалей
- •1.8. Матрицы Адамара
- •1.8.1. Определение матрицы Адамара и ее свойства
- •1.8.2. Эквивалентные преобразования матриц Адамара
- •1.8.3. Построение матриц Адамара
- •2. Основы теории конечных автоматов
- •2.1. Понятие конечного автомата
- •2.1.1. Общие сведения о конечных автоматах
- •2.1.2. Абстрактное определение конечного автомата
- •2.2. Эквивалентности в автоматах
- •2.2.1. Основные определения
- •2.2.2. Покрытия и морфизмы
- •2.2.3. Эквивалентные состояния автоматов
- •2.3. Процедура минимизации конечных автоматов
- •2.4. Автоматные функции и эксперименты с автоматами
- •2.4.1. Понятие ограниченно детерминированной функции
- •2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •2.4.3. Пример реализации конечного автомата с помощью сфэз
- •2.4.4. Эксперименты с автоматами
- •2.5. Автоматные языки
- •2.5.1. Представление о формальных языках
- •2.5.2. Алфавит, слово, язык
- •2.5.3. Классификация грамматик и языков
- •2.5.4. Понятие формальной грамматики
- •2.5.5. Автоматные грамматики
- •2.6. Модификации конечных автоматов
- •2.6.1. Частичные автоматы
- •2.6.2. Понятия недетерминированного и вероятностного автоматов
- •2.7. Процедура минимизации частичного автомата
- •2.7.1. Совместимые состояния
- •2.7.2. Техника определения совместимых состояний
- •2.7.3. Построение минимального автомата
- •3. Введение в нечеткую математику
- •3.1. Нечёткие множества
- •3.2. Нечеткие отношения
- •3.3. Нечеткая логика
- •Заключение
- •Библиографический список
- •Оглавление
- •2.7.3. Построение минимального автомата 98
- •Часть 2
- •394026 Воронеж, Московский просп., 14
- •Часть 2
1.5. Производящие функции
1.5.1. Общие сведения о производящих функциях
Для решения комбинаторных задач могут быть использованы методы математического анализа. Основой этого служит метод производящих функций. Этот метод позволяет достичь изучения свойств последовательностей. Он применяется для перечисления комбинаторных чисел и для установления комбинаторных тождеств.
Исходным
пунктом этого метода является
последовательность комбинаторных чисел
{ak}
и последовательность базисных функций
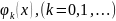 .
.
Рассмотрим формальный ряд

В
частности, если последовательность
конечна, т.е.
 ,
то ряд представляет собой многочлен.
При определенных ограничениях, ряд
будет сходиться и тогда, в некоторой
области он будет задавать функцию
,
то ряд представляет собой многочлен.
При определенных ограничениях, ряд
будет сходиться и тогда, в некоторой
области он будет задавать функцию

Функция
F(x)
называется производящей функцией
для заданной последовательности
комбинаторных чисел {ak}
относительно заданной базисной
последовательности функций
 .
.
Наиболее
часто в качестве базисной рассматривается
последовательность
 ,
(k = 0,1,..). Получающиеся
при этом производящие функции называются
обычными. Т.е. обычные производящие
функции имеют вид:
,
(k = 0,1,..). Получающиеся
при этом производящие функции называются
обычными. Т.е. обычные производящие
функции имеют вид:

В комбинаторном анализе используются также экспоненциальные производящие функции
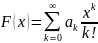 .
.
Для производящих функций по аналогии со сходящимися рядами определяются операции сложения, умножения, дифференцирования, интегрирования и т.д. при этом x является действительной или комплексной переменной. При выполнении условий сходимости производящие функции являются аналитическими.
Рассмотрим ряд примеров.
1.5.2. Производящая функция для биноминальных коэффициентов
Получим производящую
функцию для конечной последовательности
чисел, представляющих собой различное
число сочетаний изn
элементов -– .
Известно, что
.
Известно, что

и

Эти
равенства являются частными случаями
более общей формулы, дающей разложение
для
 .
Запишем
в виде
.
Запишем
в виде
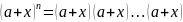
Раскроем
скобки в правой части этого равенства,
причем будем записывать все множители
в том порядке, в котором они нам встретятся.
Например, запишем в виде:
запишем в виде:

а
 -
в виде:
-
в виде:


Видно,
что в верхнюю формулу входят все
размещения с повторениями, составленные
из букв
 и
и
 по две буквы в каждом размещении, а в
нижнюю формулу - размещения с повторениями
из тех же букв, но состоящие из трех букв
каждое. То же самое и в общем случае —
после раскрытия скобок в формуле мы
получим всевозможные размещения с
повторениями букв
и
,
состоящие из
по две буквы в каждом размещении, а в
нижнюю формулу - размещения с повторениями
из тех же букв, но состоящие из трех букв
каждое. То же самое и в общем случае —
после раскрытия скобок в формуле мы
получим всевозможные размещения с
повторениями букв
и
,
состоящие из
 элементов. Приведем подобные члены.
Подобными будут члены, содержащие
одинаковое количество букв
(тогда и букв
в них будет поровну). Найдем, сколько
будет членов, в которые входит
элементов. Приведем подобные члены.
Подобными будут члены, содержащие
одинаковое количество букв
(тогда и букв
в них будет поровну). Найдем, сколько
будет членов, в которые входит
 букв
и, соответственно,
букв
и, соответственно,
 букв
.
Эти члены являются перестановками с
повторениями, составленными из
букв
и
букв
.
Поэтому их число равно
букв
.
Эти члены являются перестановками с
повторениями, составленными из
букв
и
букв
.
Поэтому их число равно

Отсюда
вытекает, что после приведения подобных
членов выражение
 войдет с коэффициентом
войдет с коэффициентом
 .
Итак, мы доказали, что
.
Итак, мы доказали, что

Это
равенство принято называть формулой
бинома Ньютона. Если положить в этом
равенстве
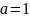 ,
то получим
,
то получим

Мы
видим, что
 является производящей функцией для
чисел
является производящей функцией для
чисел
 .
С помощью этой производящей функции
можно сравнительно просто доказать
многие свойства чисел
.
С помощью этой производящей функции
можно сравнительно просто доказать
многие свойства чисел
 .
.
Пусть
 ,
(k=0,1,…,n)
,
(k=0,1,…,n)
Тогда

В
данном случае в качестве производящей
функции выступает бином Ньютона
 .
.
Используя заданную производящую функцию, докажем тождество:

Для этого возьмем тождество
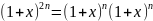
Они эквивалентны следующему

Сравнивая коэффициенты при xn, получим

