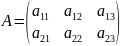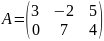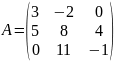- •Часть 2
- •Часть 2
- •Введение
- •1. Элементы комбинаторики
- •1.1. Простейшие комбинаторные конфигурации
- •Основные правила комбинаторики
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Латинские прямоугольники, конечные проективные плоскости и блок-схемы
- •1.2.1. Латинские прямоугольники
- •1.2.2. Конечные проективные плоскости
- •1.2.3. Блок-схемы
- •Формула включений и исключений
- •Объединение комбинаторных конфигураций
- •1.3.2. Принцип включения и исключения
- •1.3.3. Число булевых функций, существенно зависящих от всех своих переменных
- •1.3.4. Решето Эратосфена
- •Рекуррентные уравнения
- •1.4.1. Определение рекуррентного уравнения
- •1.4.2. Решение линейного однородного рекуррентного уравнения
- •1 (2) .4.3. Решение линейного неоднородного рекуррентного уравнения
- •1.5. Производящие функции
- •1.5.1. Общие сведения о производящих функциях
- •1.5.2. Производящая функция для биноминальных коэффициентов
- •1.5.3. Производящая функция для чисел Фибоначчи
- •1.6.1. Определение z – преобразования
- •1.6.2. Обратное z – преобразование
- •В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.
- •1.6.3. Свойства z-преобразования
- •1.6.4. Использование z-преобразований для решения рекуррентных уравнений
- •1.6.5. Таблица односторонних z-преобразований
- •1.7. Трансверсали и перманенты
- •1.7.1. Множества и мультимножества
- •1.7.2. Трансверсали
- •1.7.3. Пермамент матрицы
- •1.7.4. Число трансверсалей
- •1.8. Матрицы Адамара
- •1.8.1. Определение матрицы Адамара и ее свойства
- •1.8.2. Эквивалентные преобразования матриц Адамара
- •1.8.3. Построение матриц Адамара
- •2. Основы теории конечных автоматов
- •2.1. Понятие конечного автомата
- •2.1.1. Общие сведения о конечных автоматах
- •2.1.2. Абстрактное определение конечного автомата
- •2.2. Эквивалентности в автоматах
- •2.2.1. Основные определения
- •2.2.2. Покрытия и морфизмы
- •2.2.3. Эквивалентные состояния автоматов
- •2.3. Процедура минимизации конечных автоматов
- •2.4. Автоматные функции и эксперименты с автоматами
- •2.4.1. Понятие ограниченно детерминированной функции
- •2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •2.4.3. Пример реализации конечного автомата с помощью сфэз
- •2.4.4. Эксперименты с автоматами
- •2.5. Автоматные языки
- •2.5.1. Представление о формальных языках
- •2.5.2. Алфавит, слово, язык
- •2.5.3. Классификация грамматик и языков
- •2.5.4. Понятие формальной грамматики
- •2.5.5. Автоматные грамматики
- •2.6. Модификации конечных автоматов
- •2.6.1. Частичные автоматы
- •2.6.2. Понятия недетерминированного и вероятностного автоматов
- •2.7. Процедура минимизации частичного автомата
- •2.7.1. Совместимые состояния
- •2.7.2. Техника определения совместимых состояний
- •2.7.3. Построение минимального автомата
- •3. Введение в нечеткую математику
- •3.1. Нечёткие множества
- •3.2. Нечеткие отношения
- •3.3. Нечеткая логика
- •Заключение
- •Библиографический список
- •Оглавление
- •2.7.3. Построение минимального автомата 98
- •Часть 2
- •394026 Воронеж, Московский просп., 14
- •Часть 2
1.7.2. Трансверсали
Пусть
дано множество
 мощности n и множество
мощности n и множество
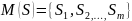 ,
элементы которого являются подмножествами
множества S, т.е.
.
,
элементы которого являются подмножествами
множества S, т.е.
.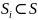 ,
, .
При этом допускается что
.
При этом допускается что
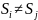 при
при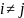
Системой
различных представителей (транверсалью)
для совокупности множеств M(S)
называется множество элементов мощности
m из множества S и таких,
что
из множества S и таких,
что
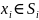 ,
,
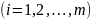
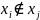 ,
при
.
,
при
.
Критерием существования трансверсали для M(S) служит следующая теорема.
Теорема
Холла. Совокупность множеств M(S)
имеет трансверсаль тогда и только тогда,
когда для любого k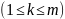 и любой k – выборки
без повторений
и любой k – выборки
без повторений
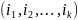 из множества
из множества
 индексов выполняется следующее
неравенство
индексов выполняется следующее
неравенство
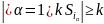
то
есть число элементов объединения
множеств
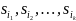 не меньше k.
не меньше k.
Если
для некоторого подсемейства
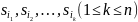 семейства M(S)
имеет место равенство
семейства M(S)
имеет место равенство

то такое подсемейство называется критическим.
1.7.3. Пермамент матрицы
Рассматривается
матрица A = (aij),
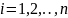 ,
,
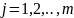 ,
,
 .
.
Перманентом матрицы A называется число, определяемое следующим выражением
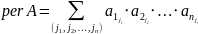
Где суммирование производится по всевозможным выборкам объема n из m различных элементов.
Рассмотрим примеры

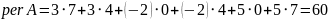

Если m = n, то суммирование производится по всевозможным перестановкам элементов 1,2,…,n ; а пермамент матрицы А (perA) получается из определителя этой матрицы при условии, что все слагаемые соответствующей суммы берутся с положительными знаками.
Свойства перманентов.
Если строка матрицы A состоит полностью из нулей, то perA=0.
Перманент матрицы инвариантен относительно любой перестановки строк и столбцов.
При умножении какой-либо строки (или столбца) на скаляр , перманент матрицы умножается на .
Если A квадратная матрица, то per AT = per A.
Если Aij получена вычеркиванием из А i – строки и j–го столбца,
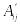 -
матрица, полученная из A
заменой элемента aij
на 0, тогда
-
матрица, полученная из A
заменой элемента aij
на 0, тогда

Разложение перманента по i – строке.
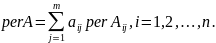
Многие свойства перманента подобны свойствам определителя для квадратных матриц, однако свойство
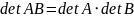 ,
,
вообще говоря, не верно для перманентов. Перманент в отличие от определителя в общем случае не равен 0 при наличии строк (столбцов), линейно выражающихся через другие строки (столбцы).
1.7.4. Число трансверсалей
Важнейшее применение перманентов определяется следующей теоремой.
Теорема.
Пусть A = (aij),
i = 1,2,..,n,
j = 1,2,..,m,
![]() ,
есть матрица инцидентности множеств
,
есть матрица инцидентности множеств
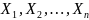 ,
являющихся подмножествами множества
,
являющихся подмножествами множества
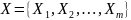 .
.
То есть
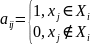
Тогда
для числа трансверсалей семейства
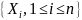 имеет место равенство
имеет место равенство

Трансверсаль
семейства
 существует тогда и только тогда, когда
для соответствующей матрицы инцидентности
выполняется условие.
существует тогда и только тогда, когда
для соответствующей матрицы инцидентности
выполняется условие.
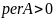
Пример
1. (задача о встречах). Требуется
определить число трансверсалей семейства
,
где Xi
= X\{i}
и x = {1,2,..,n}.
Эта задача имеет и другие разнообразные
формулировки, но обычно называется
задачей о встречах. В данном случае
матрицы инцидентности
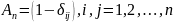 ,
где
,
где
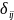 -
символ Кронекера.
-
символ Кронекера.
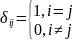
Обозначим hn = per(1-δij) и разлагая перманент по первой строке, получим
 ,
,
Где
матрица
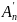 получается из матрицы
получается из матрицы
 заменой элемента a11
на 1.
заменой элемента a11
на 1.
Разлагая perA′n-1 по элементу a11, получим
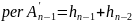
то есть получим рекуррентное соотношение
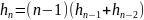
с начальными условиями h0=1 и h1=0
Перепишем рекуррентное соотношение в виде
hn-nhn-1=-(hn-1-(n-1)hn-2)=…=(-1)k(hn-k-(n-k)hn-k-1)=…=(-1)n
Полагая
 ,
получим
,
получим
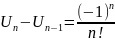
Отсюда следует что

Таким образом, окончательный ответ

Пример 2.
Требуется найти число трансверсалей семейства (Xi , 1≤i≤n), где
X1={1,2}, X2={1,2,3}, X3={2,3,4},…, Xn-1={n-2, n-1, n}, Xn={n-1, n}, являющихся подмножествами множества X={1,2,…,n}.
Решение.
Число трансверсалей

Разлагая этот перманент сначала по первой строке, а затем получившийся перманент разлагаем по первому столбцу, получаем рекуррентное соотношение
Cn=Cn-1+Cn-2
с начальным условием C1=1, C2=2
Полученные числа Cn являются числами Фибоначчи.