3. Введение в нечеткую математику

3.1. Нечёткие множества

Пусть U-универсальное множество (универсум), А – некоторое подмножество множества U т.е. 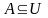. Тот факт, что элемент х множества U принадлежит подмножеству А обозначается в виде . Для выражения этой принадлежности можно воспользоваться понятием характеристической функции

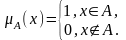
В данном случае характеристическая функция принимает только два значения 0 и 1.

Нечетким множеством А множества U называется множество упорядоченных пар

_,

где - функция принадлежности, принимающая свои значения из вполне упорядоченного множества .

Если 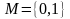, то нечеткое множество рассматривается, как обычное множество, являющиеся подмножеством универсального множества U.

Ф ункция принадлежности может задаваться графически. Для этого в прямоугольной системе координат по оси ординат откладывается значение и по оси абсцисс элементы множества U.

Рис. 11

В случае конечного множества используется следующая запись:

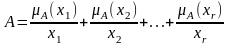
Здесь знак + обозначает объединение элементов.

Например, запись

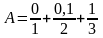
означает, что элемент универсума:

1 принадлежит А со степенью 0

2 принадлежит А со степенью 0.1

2 принадлежит А со степенью 1.0

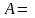
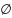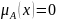
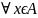Множество пусто, т.е. , если . . Нечёткое множество является универсальным (A=U), если 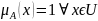/ Два множества А и В равны, т.е. А=В, если .

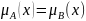Множество А включается в В, т.е. если .

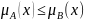Множество 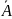есть дополнение А, если .

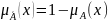Пересечение множеств А и В, если .

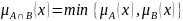Объединение .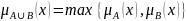

Пример

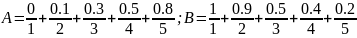
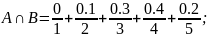
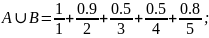
Разность нечетких множеств .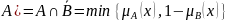

Пример

Симметричная разность нечетких множеств

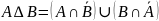
Прямое произведение нечетких множеств

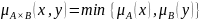
Пример

.

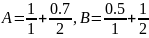Таблица 26

		B
		1		2
A	1		0.5	1
	2		0.5	0.7

Операция концентрации 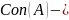возводит функцию принадлежности в квадрат.

Операция деконцентрации 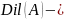извлекает квадратный корень из функции принадлежности.

3.2. Нечеткие отношения

Нечётким отношением 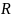на множестве называется нечеткое подмножество декартова произведения 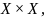характеризующиеся функциями принадлежности Значение понимается как степень выполнения отношения

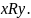
Если X конечно, то функция принадлежности представляет собой квадратную матрицу, 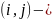элемент который означает степень выполнения отношения

Для нечеткого отношения определяется множество уровня:

Матрица множества уровня получается заменой матрицы нечеткого отношения R единицами всех элементов, значения которых не меньше а нулями все остальные элементы.

Для уровневых множеств нечетких отношений справедлива теорема от декомпозиции:

Любое нечеткое отношение R может быть представлено в форме:

Где

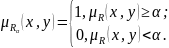
Запись 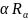означает, что все элементы обычного отношения 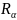умножаются на

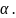
Пример

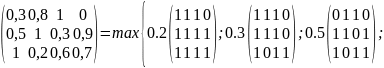
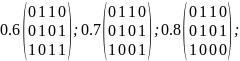
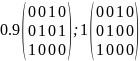
Носителем нечеткого отношения R называется обычное отношение 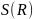такое, что

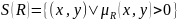
Обычное отношение, ближайшее к данному нечеткому отношению определяется следующим образом:

На нечетких отношениях вводятся отношения включения и равенства, а также операции дополнения, пересечения и объединения с помощью тех же формул, что и для нечетких множеств.

Кроме того для нечетких отношений А и В, определенных на универсуме Х, вводится операция (максимальной) композиции.

.

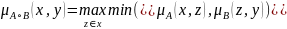Например

А В А В

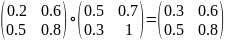
Свойства нечетких отношений

Нечеткое отношение R называется:

1. Рефлексивным, если

2. Симметричным, если

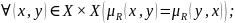
3. Антисимметричным, если или

4. Несимметрично, если

5. Совершенно антисимметричным, если

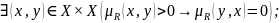
6. (максимально) транзитивным, если

Транзитивным замыканием нечетного бинарного отношения R называется отношение 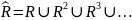. Если то

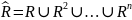
Виды нечетких отношений

Нечеткие отношения предпорядка – это то, которое обладает свойствами транзитивности и рефлективности.

Нечеткое отношение нестрогого порядка – это то, которое обладает свойствами транзитивности, антисимметричности и рефлективности.

Нечеткое отношение строгого порядка – транзитивное, антисимметричное и антирефлексивное отношение.

Рефлексивное и симметричное отношение называется отношением сходства.

Нечеткое отношение, обладающее свойствами рефлективности, симметричности и транзитивности называются отношениями подобия (нечетким отношением эквивалентности)