
- •Часть 2
- •Часть 2
- •Введение
- •1. Элементы комбинаторики
- •1.1. Простейшие комбинаторные конфигурации
- •Основные правила комбинаторики
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Латинские прямоугольники, конечные проективные плоскости и блок-схемы
- •1.2.1. Латинские прямоугольники
- •1.2.2. Конечные проективные плоскости
- •1.2.3. Блок-схемы
- •Формула включений и исключений
- •Объединение комбинаторных конфигураций
- •1.3.2. Принцип включения и исключения
- •1.3.3. Число булевых функций, существенно зависящих от всех своих переменных
- •1.3.4. Решето Эратосфена
- •Рекуррентные уравнения
- •1.4.1. Определение рекуррентного уравнения
- •1.4.2. Решение линейного однородного рекуррентного уравнения
- •1 (2) .4.3. Решение линейного неоднородного рекуррентного уравнения
- •1.5. Производящие функции
- •1.5.1. Общие сведения о производящих функциях
- •1.5.2. Производящая функция для биноминальных коэффициентов
- •1.5.3. Производящая функция для чисел Фибоначчи
- •1.6.1. Определение z – преобразования
- •1.6.2. Обратное z – преобразование
- •В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.
- •1.6.3. Свойства z-преобразования
- •1.6.4. Использование z-преобразований для решения рекуррентных уравнений
- •1.6.5. Таблица односторонних z-преобразований
- •1.7. Трансверсали и перманенты
- •1.7.1. Множества и мультимножества
- •1.7.2. Трансверсали
- •1.7.3. Пермамент матрицы
- •1.7.4. Число трансверсалей
- •1.8. Матрицы Адамара
- •1.8.1. Определение матрицы Адамара и ее свойства
- •1.8.2. Эквивалентные преобразования матриц Адамара
- •1.8.3. Построение матриц Адамара
- •2. Основы теории конечных автоматов
- •2.1. Понятие конечного автомата
- •2.1.1. Общие сведения о конечных автоматах
- •2.1.2. Абстрактное определение конечного автомата
- •2.2. Эквивалентности в автоматах
- •2.2.1. Основные определения
- •2.2.2. Покрытия и морфизмы
- •2.2.3. Эквивалентные состояния автоматов
- •2.3. Процедура минимизации конечных автоматов
- •2.4. Автоматные функции и эксперименты с автоматами
- •2.4.1. Понятие ограниченно детерминированной функции
- •2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •2.4.3. Пример реализации конечного автомата с помощью сфэз
- •2.4.4. Эксперименты с автоматами
- •2.5. Автоматные языки
- •2.5.1. Представление о формальных языках
- •2.5.2. Алфавит, слово, язык
- •2.5.3. Классификация грамматик и языков
- •2.5.4. Понятие формальной грамматики
- •2.5.5. Автоматные грамматики
- •2.6. Модификации конечных автоматов
- •2.6.1. Частичные автоматы
- •2.6.2. Понятия недетерминированного и вероятностного автоматов
- •2.7. Процедура минимизации частичного автомата
- •2.7.1. Совместимые состояния
- •2.7.2. Техника определения совместимых состояний
- •2.7.3. Построение минимального автомата
- •3. Введение в нечеткую математику
- •3.1. Нечёткие множества
- •3.2. Нечеткие отношения
- •3.3. Нечеткая логика
- •Заключение
- •Библиографический список
- •Оглавление
- •2.7.3. Построение минимального автомата 98
- •Часть 2
- •394026 Воронеж, Московский просп., 14
- •Часть 2
2.6.1. Частичные автоматы
В
определении конечного автомата![]() предполагается, что функции
и
всюду определены. Однако на практике,
встречаются случаи, когда они лишь
частично определены. Это связано с тем,
что сложные системы проектируются по
частям и поэтому может оказаться, что
некоторые входные строки либо вообще
не встречаются, либо встречаются в
случаях, когда их выход нас не интересует.
Это приводит к тому, что некоторые
позиции в таблицах состояний (или ребра
в диаграммах состояний) отсутствуют.
Такие позиции называются безразличными,
т.к. нас не интересуют их содержания. В
таблицах состояний они обозначается
прочерками.
предполагается, что функции
и
всюду определены. Однако на практике,
встречаются случаи, когда они лишь
частично определены. Это связано с тем,
что сложные системы проектируются по
частям и поэтому может оказаться, что
некоторые входные строки либо вообще
не встречаются, либо встречаются в
случаях, когда их выход нас не интересует.
Это приводит к тому, что некоторые
позиции в таблицах состояний (или ребра
в диаграммах состояний) отсутствуют.
Такие позиции называются безразличными,
т.к. нас не интересуют их содержания. В
таблицах состояний они обозначается
прочерками.
Например, это имеется в таблице
Таблица 17
Текущее состояние |
Следующее состояние |
Выход |
||
0 |
1 |
0 |
1 |
|
|
|
|
0 |
1 |
|
- |
|
1 |
0 |
|
|
|
- |
1 |
В данном случае безразлично состояние автомата начавшего работу из состояния , и считавшего входной символ 0, так же безразличен выход автомата, находящегося в состоянии и считавшего символ 0.
Для представления способа минимизации не полностью описанных автоматов используются следующие определения.
Определение
1. Входная последовательность
![]() называется допустимой для автомата
находившегося в начальном состоянии
,
если функция перехода
определена для всех элементов
последовательности, кроме возможно
последнего. т.е, допустимая входная
строка автомата с начальным состоянием
,
однозначно определяет строку внутренних
состояний, за исключением последнего
состояния, которое может быть неопределенным
(безразличным).
называется допустимой для автомата
находившегося в начальном состоянии
,
если функция перехода
определена для всех элементов
последовательности, кроме возможно
последнего. т.е, допустимая входная
строка автомата с начальным состоянием
,
однозначно определяет строку внутренних
состояний, за исключением последнего
состояния, которое может быть неопределенным
(безразличным).
Определение
2. Выходная строка
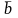 покрывает выходную строку
покрывает выходную строку
 (в которой могут быть неопределенные
символы), если любой символ
(в которой могут быть неопределенные
символы), если любой символ
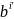 из
равен соответствующему символу
из
равен соответствующему символу
 из
.
Например, строка
из
.
Например, строка
 покрывает строку
покрывает строку
 ;
строка 010 покрывает -10, строка 110 покрывает
110 и -10. Если
покрывает
,
то пишут, что
;
строка 010 покрывает -10, строка 110 покрывает
110 и -10. Если
покрывает
,
то пишут, что
 .
.
Определение
3. Если
![]() ,
допустимых для
,
допустимых для
![]() ,
то говорят, что
,
то говорят, что
![]() покрывает
,
и пишут
покрывает
,
и пишут
![]() .
.
Определение
4. Автомат
![]() покрывает
покрывает
![]() ,
если
,
если
![]() автомата
существует
такое состояние
автомата
,
что
автомата
существует
такое состояние
автомата
,
что
![]() .
Другими словами, каждое состояние
автомата
покрывается некоторым состоянием
автомата
.
В этом случае пишут
.
Другими словами, каждое состояние
автомата
покрывается некоторым состоянием
автомата
.
В этом случае пишут
![]()
Пример. Имеются два автомата
Автомат М Таблица 18
Текущее состояние |
Следующее состояние |
Выход |
||
0 |
1 |
0 |
1 |
|
|
|
|
0 |
1 |
|
|
|
- |
1 |
|
|
|
1 |
1 |
Автомат
 Таблица 19
Таблица 19
Текущее состояние |
Следующее состояние |
Выход |
||
0 |
1 |
0 |
1 |
|
|
|
|
0 |
1 |
|
|
|
1 |
1 |
, Автомат покрывает , т.к. состояния покрывает и , а состояние покрывает .
Заметим, что входная последовательность 01010, считанная автоматом , находящимся в начальном состоянии , перерабатывается в -111-, а считанная в начальном состоянии перерабатывается в 01111. При этом первый безразличный символ на выходе отвечает 0 в , а второй – соответствует 1 в . Таким образом, в ходе работы безразличная позиция в таблице для автомата может заполняться как нулем, так и единицей.
Определение
5. Выходная строка
совместима с выходной строкой
,
если в каждой позиции, где символы обеих
строк определены, они совпадают. Пишут
 ,
если строка
совместима
со строкой
.
,
если строка
совместима
со строкой
.
Примеры. Строка 01-1 совместима с 0111; строка 0-1- совместима с 011-; но строка 010- несовместима с 011-.
Отметим,
что отношение совместимости
![]() не является отношением эквивалентности,
так как оно рефлексивно, симметрично,
но не транзитивно.
не является отношением эквивалентности,
так как оно рефлексивно, симметрично,
но не транзитивно.


