
- •Часть 2
- •Часть 2
- •Введение
- •1. Элементы комбинаторики
- •1.1. Простейшие комбинаторные конфигурации
- •Основные правила комбинаторики
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Латинские прямоугольники, конечные проективные плоскости и блок-схемы
- •1.2.1. Латинские прямоугольники
- •1.2.2. Конечные проективные плоскости
- •1.2.3. Блок-схемы
- •Формула включений и исключений
- •Объединение комбинаторных конфигураций
- •1.3.2. Принцип включения и исключения
- •1.3.3. Число булевых функций, существенно зависящих от всех своих переменных
- •1.3.4. Решето Эратосфена
- •Рекуррентные уравнения
- •1.4.1. Определение рекуррентного уравнения
- •1.4.2. Решение линейного однородного рекуррентного уравнения
- •1 (2) .4.3. Решение линейного неоднородного рекуррентного уравнения
- •1.5. Производящие функции
- •1.5.1. Общие сведения о производящих функциях
- •1.5.2. Производящая функция для биноминальных коэффициентов
- •1.5.3. Производящая функция для чисел Фибоначчи
- •1.6.1. Определение z – преобразования
- •1.6.2. Обратное z – преобразование
- •В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.
- •1.6.3. Свойства z-преобразования
- •1.6.4. Использование z-преобразований для решения рекуррентных уравнений
- •1.6.5. Таблица односторонних z-преобразований
- •1.7. Трансверсали и перманенты
- •1.7.1. Множества и мультимножества
- •1.7.2. Трансверсали
- •1.7.3. Пермамент матрицы
- •1.7.4. Число трансверсалей
- •1.8. Матрицы Адамара
- •1.8.1. Определение матрицы Адамара и ее свойства
- •1.8.2. Эквивалентные преобразования матриц Адамара
- •1.8.3. Построение матриц Адамара
- •2. Основы теории конечных автоматов
- •2.1. Понятие конечного автомата
- •2.1.1. Общие сведения о конечных автоматах
- •2.1.2. Абстрактное определение конечного автомата
- •2.2. Эквивалентности в автоматах
- •2.2.1. Основные определения
- •2.2.2. Покрытия и морфизмы
- •2.2.3. Эквивалентные состояния автоматов
- •2.3. Процедура минимизации конечных автоматов
- •2.4. Автоматные функции и эксперименты с автоматами
- •2.4.1. Понятие ограниченно детерминированной функции
- •2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •2.4.3. Пример реализации конечного автомата с помощью сфэз
- •2.4.4. Эксперименты с автоматами
- •2.5. Автоматные языки
- •2.5.1. Представление о формальных языках
- •2.5.2. Алфавит, слово, язык
- •2.5.3. Классификация грамматик и языков
- •2.5.4. Понятие формальной грамматики
- •2.5.5. Автоматные грамматики
- •2.6. Модификации конечных автоматов
- •2.6.1. Частичные автоматы
- •2.6.2. Понятия недетерминированного и вероятностного автоматов
- •2.7. Процедура минимизации частичного автомата
- •2.7.1. Совместимые состояния
- •2.7.2. Техника определения совместимых состояний
- •2.7.3. Построение минимального автомата
- •3. Введение в нечеткую математику
- •3.1. Нечёткие множества
- •3.2. Нечеткие отношения
- •3.3. Нечеткая логика
- •Заключение
- •Библиографический список
- •Оглавление
- •2.7.3. Построение минимального автомата 98
- •Часть 2
- •394026 Воронеж, Московский просп., 14
- •Часть 2
2.5.5. Автоматные грамматики
Рассмотрим
языки, которые «принимаются» или
«распознаются» автоматами с конечным
числом состояний. Такой автомат после
считывания символа
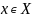 из состояния s переходит в новое
состояние
из состояния s переходит в новое
состояние
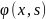 .
Считав последний символ, автомат
останавливается. Если он остановился
в одном из «принимающих» состояний из
отмеченного множества F,
входная строка считается принятой.
Если конечное состояние автомата лежит
в
.
Считав последний символ, автомат
останавливается. Если он остановился
в одном из «принимающих» состояний из
отмеченного множества F,
входная строка считается принятой.
Если конечное состояние автомата лежит
в
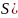 ,
то строка считается отвергнутой.
Рассмотрим формальное определение.
,
то строка считается отвергнутой.
Рассмотрим формальное определение.
Акцептором
с конечным числом состояний (конечным
акцептором, анализатором) называется
пятерка
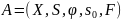 ,
где:
,
где:
 -
конечное множество входных символов,
-
конечное множество входных символов,
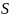 -
конечное множество внутренних состояний,
-
конечное множество внутренних состояний,
-
функция из
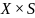 в
,
в
,
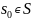 – начальное
состояние
– начальное
состояние
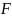 -
множество принимающих состояний, где
-
множество принимающих состояний, где
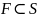 .
.
Входные символы линейно упорядочены, так как они напечатаны на входной ленте, и последовательно считываются читающей головкой. Пример конечного акцептора, заданного с помощью графа.

Рис. 9
Данный акцептор принимает, такие строки как 001, 0001, 100, 1010, 10110.
Рассмотрим класс грамматики, порождающих в точности такие множества строк, которые принимаются некоторым конечным акцептором.
Определение.
Автоматной грамматикой называется
четверка
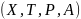 ,
где
,
где
– конечное множество входных символов,
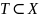 – конечное множество
терминальных символов,
– конечное множество
терминальных символов,
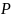 – конечное множество
правил порождения вида
– конечное множество
правил порождения вида
 ,
,
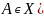 – отмеченный
начальный символ.
– отмеченный
начальный символ.
Небольшие конечные акцепторы, а также автоматные грамматики, удобно изображать с помощью диаграмм состояний.
Для составления диаграммы состояний автоматной грамматики – следует произвести следующие действия:
Шаг
1. Каждому нетерминальному символу из
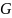 постaвить в соответствие вершину
графа.
постaвить в соответствие вершину
графа.
Шаг
2. Каждому правилу
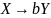 поставить в соответствие дугу от вершины
к
поставить в соответствие дугу от вершины
к
 вершине,
помеченную символом b.
вершине,
помеченную символом b.
Шаг
3. Каждому правилу поставить в соответствие дугу от вершины
к
новой вершине, с пометкой ПРИНЯТЬ.
поставить в соответствие дугу от вершины
к
новой вершине, с пометкой ПРИНЯТЬ.
Пример. На рисунке показана диаграмма состояний (помеченный ориентированный граф), отвечающая автоматной грамматике G с правилами.
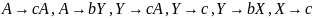

X
Рис. 10
Для автоматных грамматик справедливы утверждения.
Последовательность меток дуг вдоль любого конечного пути, начинающегося из вершины А, на диаграмме грамматики G, является строкой, порождаемой G, и, наоборот, все порождаемые строки соответствуют некоторым путям.
Для любой автоматной грамматики существует конечный акцептор, принимающий в точности те строки, которые порождает грамматика.
Для любого конечного акцептора существует автоматная грамматика, порождающая в точности те строки, которые принимаются этим акцептором.
Существуют контекстно-свободные языки, не являющиеся автоматными языками.
2.6. Модификации конечных автоматов
Существуют многочисленные модификации конечных автоматов. С одной из них мы уже знакомились – это машины Тьюринга. Рассмотрим модификации, связанные с обобщениями переходной и выходной функций. Для них допускается произвольные отношения, случайные функции и т.п. В частности, к таким модификациям относятся частичные, недетерминированные и вероятные автоматы.
