2.5.4. Понятие формальной грамматики

Формальная грамматика применяется в математической лингвистике для описания естественных и искусственных языков.

Формальная грамматика — система правил, описывающая множество конечных последовательностей символов. Конечные последовательности (цепочки), входящие в указанное множество, называются предложениями, а само множество — языком, описываемым данной формальной грамматикой. Различают два типа формальных грамматик:

1. Грамматики порождающие — это системы правил, позволяющие строить предложения языка.

2. Грамматики распознающие — это алгоритм, распознающие по любой цепочке, является ли она предложением или нет.

Определение. Порождающей грамматикой называется четверка 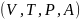, где V — конечный алфавит, состоящий из символов, – подмножество терминальных символов, - выделенный нетерминальный символ, обозначающий совокупность всех порождаемых объектов; P- конечное множество правил порождения вида u→ν, где u — непустая строка нетерминальных символов, а ν — некоторая строка.

Множество всех строк терминальных символов, которые можно получить применением правил порождения, называется языком. Оно является подмножеством 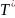множества — всех строк символов из T.

В приложениях к грамматике естественных языков терминальными считаются обычные слова, а символы из 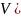— есть названия частей речи и других грамматических категорий. Правила порождения здесь могут быть следующего типа А = <предложение> →<подлежащее><сказуемое> и правила подстановки типа <подлежащее> →<мальчик> и <сказуемое>→ <улыбается>. Строки терминальных символов языка являются грамматически правильными предложениями.

В языках символической логики некоторые правила порождения 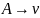называются аксиомами, а другие - «правилами вывода». «Предложения», которые можно породить с помощью правил вывода и аксиом, называются теоремами рассматриваемой дедуктивной системы.

Рассмотри примеры порождающих грамматик с ,т.е. грамматик с единственной грамматической категорией.

1. Пусть 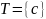и P состоит из двух правил порождения 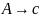, 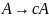. Эта грамматика порождает язык , т.е. множество состоит из всех конечных строк, составленных из символа C.

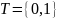2. Пусть и P состоит из следующих правил порождения:

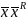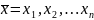,где ∧— пустая строка, которая подчиняется правилу , т.е. она исчезает в любой непустой строке. Эта грамматика порождает пустую строку и две двоичные последовательности вида , где , а 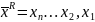— обращение строки .

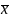3. Пусть 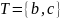и 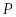состоит из правил порождения , 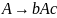. Она порождает язык .

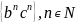4. Пусть , а P состоит из правил порождения 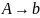, , . Она порождает язык, состоящий из всех строк в, закончившихся на b.

Определение. Правило порождения 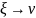называется контекстно –свободным, если оно применимо к любой строке вида 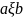и дает строку . Язык, который порождается лишь контекстно-свободными правилами, называется контекстно-свободным.

Если разрешается применять правило к строке лишь при некоторых a и b, то это правило называется зависящим от контекста. Заметим, что правила естественных языков в сильной степени зависят от контекста, а искусственные языки обычно являются контекстно-свободными.