
- •Часть 2
- •Часть 2
- •Введение
- •1. Элементы комбинаторики
- •1.1. Простейшие комбинаторные конфигурации
- •Основные правила комбинаторики
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Латинские прямоугольники, конечные проективные плоскости и блок-схемы
- •1.2.1. Латинские прямоугольники
- •1.2.2. Конечные проективные плоскости
- •1.2.3. Блок-схемы
- •Формула включений и исключений
- •Объединение комбинаторных конфигураций
- •1.3.2. Принцип включения и исключения
- •1.3.3. Число булевых функций, существенно зависящих от всех своих переменных
- •1.3.4. Решето Эратосфена
- •Рекуррентные уравнения
- •1.4.1. Определение рекуррентного уравнения
- •1.4.2. Решение линейного однородного рекуррентного уравнения
- •1 (2) .4.3. Решение линейного неоднородного рекуррентного уравнения
- •1.5. Производящие функции
- •1.5.1. Общие сведения о производящих функциях
- •1.5.2. Производящая функция для биноминальных коэффициентов
- •1.5.3. Производящая функция для чисел Фибоначчи
- •1.6.1. Определение z – преобразования
- •1.6.2. Обратное z – преобразование
- •В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.
- •1.6.3. Свойства z-преобразования
- •1.6.4. Использование z-преобразований для решения рекуррентных уравнений
- •1.6.5. Таблица односторонних z-преобразований
- •1.7. Трансверсали и перманенты
- •1.7.1. Множества и мультимножества
- •1.7.2. Трансверсали
- •1.7.3. Пермамент матрицы
- •1.7.4. Число трансверсалей
- •1.8. Матрицы Адамара
- •1.8.1. Определение матрицы Адамара и ее свойства
- •1.8.2. Эквивалентные преобразования матриц Адамара
- •1.8.3. Построение матриц Адамара
- •2. Основы теории конечных автоматов
- •2.1. Понятие конечного автомата
- •2.1.1. Общие сведения о конечных автоматах
- •2.1.2. Абстрактное определение конечного автомата
- •2.2. Эквивалентности в автоматах
- •2.2.1. Основные определения
- •2.2.2. Покрытия и морфизмы
- •2.2.3. Эквивалентные состояния автоматов
- •2.3. Процедура минимизации конечных автоматов
- •2.4. Автоматные функции и эксперименты с автоматами
- •2.4.1. Понятие ограниченно детерминированной функции
- •2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •2.4.3. Пример реализации конечного автомата с помощью сфэз
- •2.4.4. Эксперименты с автоматами
- •2.5. Автоматные языки
- •2.5.1. Представление о формальных языках
- •2.5.2. Алфавит, слово, язык
- •2.5.3. Классификация грамматик и языков
- •2.5.4. Понятие формальной грамматики
- •2.5.5. Автоматные грамматики
- •2.6. Модификации конечных автоматов
- •2.6.1. Частичные автоматы
- •2.6.2. Понятия недетерминированного и вероятностного автоматов
- •2.7. Процедура минимизации частичного автомата
- •2.7.1. Совместимые состояния
- •2.7.2. Техника определения совместимых состояний
- •2.7.3. Построение минимального автомата
- •3. Введение в нечеткую математику
- •3.1. Нечёткие множества
- •3.2. Нечеткие отношения
- •3.3. Нечеткая логика
- •Заключение
- •Библиографический список
- •Оглавление
- •2.7.3. Построение минимального автомата 98
- •Часть 2
- •394026 Воронеж, Московский просп., 14
- •Часть 2
2.5.2. Алфавит, слово, язык
Рассмотрим самое простое понятие теории языков — понятие алфавита.
Алфавит
— это произвольное непустое конечное
множество
 ,
элементы которого называют буквами
или символами. Обычно задают
определенную нумерацию алфавита
(как, скажем, для русского алфавита: „а»
— первая буква, „б» — вторая и т.д. до
33-й — „я»). Впредь договоримся, фиксируя
алфавит, записывать его буквы в порядке
их номеров.
,
элементы которого называют буквами
или символами. Обычно задают
определенную нумерацию алфавита
(как, скажем, для русского алфавита: „а»
— первая буква, „б» — вторая и т.д. до
33-й — „я»). Впредь договоримся, фиксируя
алфавит, записывать его буквы в порядке
их номеров.
Определение:
Словом или цепочкой в алфавите
V называют произвольный кортеж из
множества
 (k-й декартовой степени алфавита V)
для различных k =
0,1,2,…
(k-й декартовой степени алфавита V)
для различных k =
0,1,2,…
Например, если V={а,b,с}, то (а), (b), (с), (а, b), (а, b, с),
(с, b, а, а, с) и т.д. есть слова в V.
При
k = 0 получаем пустой кортеж,
называемый в данном контексте пустым
словом или пустой цепочкой и
обозначаемый
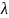 .
Множество всех слов в алфавите V
обозначают
.
Множество всех слов в алфавите V
обозначают
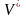 ,
а множество всех непустых слов в V
— как
,
а множество всех непустых слов в V
— как
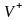 .
Слова, ради удобства чтения и простоты
записи, будем записывать без скобок и
запятых. Так, для записанных выше слов
получим: а, b, с, аb, аbс, сbаас.
.
Слова, ради удобства чтения и простоты
записи, будем записывать без скобок и
запятых. Так, для записанных выше слов
получим: а, b, с, аb, аbс, сbаас.
Такая запись слова согласуется с его интуитивным пониманием как цепочки следующих друг за другом символов. Тогда пустое слово — это слово, не имеющее символов, „пустой лист бумаги», на котором еще ничего не написано.
По
определению, длина слова v
— число компонент кортежа,
т.е. если
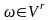 то
длина слова
то
длина слова
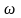 равна r. Длину слова
договоримся обозначать |
|.
Ясно, что для пустого слова |
равна r. Длину слова
договоримся обозначать |
|.
Ясно, что для пустого слова |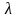 |
= 0. Длину слова тем самым можно понимать
как число составляющих это слово букв.
|
= 0. Длину слова тем самым можно понимать
как число составляющих это слово букв.
Докажем, что множество V* счетно. Для этого достаточно построить какую-либо нумерацию этого множества. Рассмотрим здесь нумерацию, называемую лексикографической.
В
данной нумерации пустому слову
присваивается номер 0, а буквам
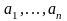 алфавита
V — номера 1, …, n соответственно.
Если слово х имеет лексикографический
номер
алфавита
V — номера 1, …, n соответственно.
Если слово х имеет лексикографический
номер
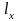 ,
то слову
,
то слову
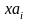 присваивается
номер
присваивается
номер
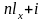 .
Отсюда следует, что лексикографический
номер слова
.
Отсюда следует, что лексикографический
номер слова
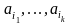 будет
равен
будет
равен
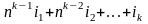

Заметим, что последняя сумма напоминает запись числа в системе счисления по модулю n (мощности алфавита) с тем лишь различием, что используется цифра n, но не допускается цифра 0. Итак, по любому слову в алфавите V однозначно вычисляется его лексикографический номер. Обратно, любое натуральное число однозначно раскладывается по степеням п указанным выше образом.
Действительно,
если дано число N, то
при
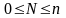 оно
служит номером пустого слова (N
= 0) или некоторой буквы алфавита. Иначе
представим N в виде
оно
служит номером пустого слова (N
= 0) или некоторой буквы алфавита. Иначе
представим N в виде
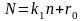
где
 .
.
Если
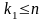 ,
то N есть номер слова
,
то N есть номер слова
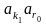 .
Иначе раскладываем
в виде
.
Иначе раскладываем
в виде

где
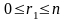 .
Тогда
.
Тогда

С числом поступаем точно так же, как и с . После конечного числа шагов получим разложение числа N в виде
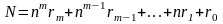
где
каждое число
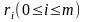 находится в диапазоне от 1 до n.
находится в диапазоне от 1 до n.
По полученному разложению N однозначно восстанавливается слово в V, имеющее номер N:
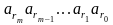
2.5.3. Классификация грамматик и языков
Единственное ограничение, накладываемое на правило вывода любой грамматики, состоит в том, что в левую часть правила должен входить хотя бы один нетерминал. В зависимости от дополнительных ограничений, накладываемых на правила вывода грамматики, различают следующие основные классы грамматик.
1. Грамматики типа 0, или грамматики общего вида. Здесь на правила вывода не накладывается никаких дополнительных ограничений.
2.
Неукорачивающие грамматики.
Каждое правило такой грамматики имеет
вид
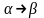 ,
где
,
где
 .
Таким образом, длина правой части правила
не меньше длины левой.
.
Таким образом, длина правой части правила
не меньше длины левой.
3. Контекстно-зависимые
грамматики (К3-грамматики).
Грамматику называют контекстно-зависимой
грамматикой (КЗ-грамматикой), если любое
ее правило вывода имеет вид
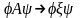 ,
где А — нетерминал,
,
где А — нетерминал,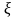 — некоторая цепочка,
— некоторая цепочка,
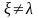 .
Каждое такое правило, называемое
КЗ-правилом, позволяет заменить
нетерминал А в „контексте», образуемом
цепочками
и
в объединенном алфавите, непустой
цепочкой
.
Иногда цепочку
называют левым контекстом, а цепочку
—
правым контекстом данного КЗ-правила.
Из определения видно, что каждая
КЗ-грамматика является неукорачивающей.
.
Каждое такое правило, называемое
КЗ-правилом, позволяет заменить
нетерминал А в „контексте», образуемом
цепочками
и
в объединенном алфавите, непустой
цепочкой
.
Иногда цепочку
называют левым контекстом, а цепочку
—
правым контекстом данного КЗ-правила.
Из определения видно, что каждая
КЗ-грамматика является неукорачивающей.
Если в КЗ-правиле снять требование непустоты цепочки , то получим грамматику, которую называют обобщенной КЗ-грамматикой (или, коротко, ОКЗ-грамматикой).
4.
Контекстно-свободные грамматики
(КС-грамматики). Каждое правило
такой грамматики имеет вид
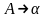 ,
т.е. левая часть каждого правила вывода
есть нетерминал, а правая — произвольная
(может быть и пустая) цепочка в объединенном
алфавите. С практической точки зрения
это наиболее важный класс грамматик,
поскольку именно в терминах КС-грамматик
описывается синтаксис языков
программирования.
,
т.е. левая часть каждого правила вывода
есть нетерминал, а правая — произвольная
(может быть и пустая) цепочка в объединенном
алфавите. С практической точки зрения
это наиболее важный класс грамматик,
поскольку именно в терминах КС-грамматик
описывается синтаксис языков
программирования.
5.
Линейные грамматики. Каждое
правило такой грамматики имеет вид
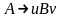 или
или
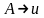 т.е. в правой части правила может
содержаться не более одного вхождения
нетерминала. Если во всех правилах вида
имеет место
т.е. в правой части правила может
содержаться не более одного вхождения
нетерминала. Если во всех правилах вида
имеет место
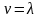 ,
то грамматика называется праволинейной,
а если
,
то грамматика называется праволинейной,
а если
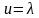 —леволинейной.
—леволинейной.
