2.2. Эквивалентности в автоматах

2.2.1. Основные определения

Пусть на вход конечного автомата подается последовательность символов из входного алфавита . Эту последовательность обозначают , и называют строкой или вектором.

На выходе конечного автомата печатается выходная строка

,

состоящая из символов алфавита .

Строка внутренних состояний .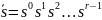

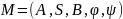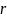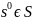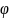Для некоторого автомата по любой входной строки длины , и по любому начальному состоянию однозначно определяется строка длины внутренних состояний. , которая получается применением отображения , т.е.

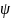Аналогично, выходная строка определяется последовательным применением отображения , т.е.

Поэтому рассматривая конечный автомат, как устройство, перерабатывающее пары 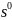и в строки и ,

Можно определить функции

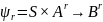
Эти функции рекурсивно строятся по известным φ и ψ, задающихся в описании автомата M.

Здесь A^r – множество всех строк длины r из алфавита A, а

B^r и S^r – множества всех строк длины r из алфавитов B и S соответственно

Пример. Рассмотрим автомат с двумя устойчивыми состояниями, изображенный на рисунке

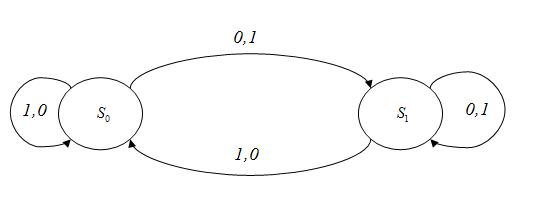
Рис. 6

Здесь заданы: входная строка 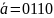и начальное состояние . Отсюда получим:

.

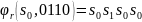
В реальных устройствах увеличение числа внутренних состояний автомата приводит к росту числа электронных схем и следовательно, к уменьшению надёжности, к усложнению ремонта и т.д. Поэтому число необходимых состояний автомата стремятся уменьшить, не ограничивая его возможностей. В связи с этим важна следующая задача.

Пусть фиксированы входной и выходной алфавиты. Можно ли заменить автомат автоматом с меньшим числом состояний 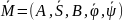, но с той же функцией, переводящей входы в выходы.

Определение. Автомат покрывает автомат , если входной и выходной алфавиты у этих автоматов общие и существует функция 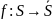, такая что для любого положительного числа r

Указанный факт записывается в виде .

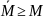Автомат, который нельзя покрыть меньшим автоматом называется минимальным. Можно проверить, что отношение покрытия является рефлексивным и транзитивным.

Автоматы и называются эквивалентными, если покрывает и одновременно с этим покрывает . В этом случае пишут .

Эквивалентность автоматов означает, что существуют функции f и g такие, что

со свойством

со свойством .

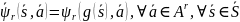Следствие Отношение эквивалентности автоматов симметрично, транзитивно, рефлексивно.

2.2.2. Покрытия и морфизмы

Отношения покрытия и эквивалентности тесно связаны с понятием морфизма.

Пусть имеются автоматы и с общими входными и выходными алфавитами.

Морфизмом называют отображение , такое, что 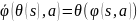и

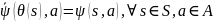
Если θ сюрьективно, то морфизм называется эпиморфизмом. Если θ биективно, то морфизм называется изоморфизмом (автоматом).

Пусть отображение θ – эпиморфизм автомата на . Тогда для любой входной строки 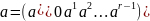и начального состояния 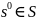выходная строка 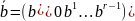автомата совпадает с выходной строкой , если начальное состояние удовлетворяет условию .

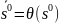Таким образом, любой эпиморфизм автоматов 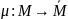определяет покрытие автомата автоматом .

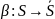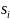Определение. Автоматы и , имеющие общие алфавиты и изоморфны, если: 1) у них одинаковое число внутренних состояний и 2)существует биекция такая, что любая входная строка перерабатывается в одну и ту же выходную строку автоматами и с начальными состояниями и .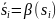 соответственно.

Например, автоматы, представленные на рисунке изоморфны, так как имеет место биекция и .

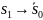
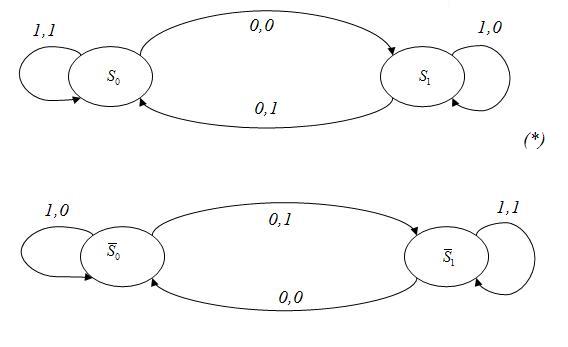
Рис. 7