
- •Введение
- •Определители, матрицы. Системы линейных уравнений
- •2. Линейные пространства.
- •Решение систем линейных уравнений
- •3. Подпространства, образованные решениями линейной однородной системы (лос) уравнений. Нахождение общего решения лос
- •4. Линейные преобразования и действия Над ними
- •5. Собственные значения и собственые векторы матрицы
- •6. Приведение квадратичной формы к каноническому виду
- •7. Векторы и действия над ними
- •8. Плоскость и прямая в пространстве
- •9. Кривые второго порядка на плоскости
- •10. Приведение общего уравнения кривой второго порядка к каноническому виду
- •11. Исследование общего уравнения кривой. Поверхности второго порядка.
- •12. Комплексные числа. Теорема
- •И ее предел.
- •13. Функция. Предел функции
- •14. Применение эквивалентных бесконечно малых к вычислению пределов
- •15. Производная функции и ее вычисление
- •16. Дифференциал функции. Применение дифференциала
- •17. Неопределенный интеграл
- •18. Определенный интеграл
- •19. Несобственные интегралы
- •20. Приложения определённого интеграла
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •21. Функции нескольких переменных Основные теоретические сведения
- •22. Частные производные первого порядка. Полный дифференциал функции и его применение к приближенным вычислениям
- •1) Случай одной независимой переменной.
- •23. Производные и дифференциалы высших порядков
- •1) Случай одной независимой переменной.
- •2) Случай нескольких независимых переменных.
- •24. Формула Тейлора для функции двух переменных
- •25. Экстремум функции нескольких независимых переменных
- •26. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •27. Дифференциальные уравнения
- •28. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •29. ЧиСлоВые ряды
- •30. Функциональные ряды
- •31. Тригонометрические ряды Фурье
- •32. Интеграл Фурье
- •33. Двойной интеграл
- •34. Тройные интегралы
- •35. Криволинейные интегралы
- •36. Поверхностные интегралы
- •Поверхностные интегралы второго рода
- •Так же получены формулы:
- •37. Теория поля
- •Скалярные поля
- •Формула Остроградского на плоскости
- •Циркуляция вектора вдоль контура не зависит от выбора координатной системы.
- •38. Оператор Гамильтона
- •Дифференциальные операции второго порядка
- •39. Функция комплексного переменного
- •40. Дифференцирование функций комплексного переменного, условия коши — римана
- •41. Интегрирование функций комплексного переменного
- •42. Ряд лорана
- •43. Преобразование Лапласа
- •44. Задача коши для обыкновенных линейных дифференциальных уравнений
- •Заключение
- •Библиографический список
- •35. Криволинейные интегралы ……………………………….302
- •394026 Воронеж, Московский просп.,14
9. Кривые второго порядка на плоскости
1.Окружность – это множество точек плоскости, равноудаленных от данной точки (центра). Если R – радиус окружности, точки M0 (x0,y0) - ее центр, то каноническое уравнение окружности имеет вид : (x-x0)2+(y-y0)2=R2 .
2. Эллипс – это множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а, причем эта постоянная больше расстояния между фокусами (рис.9.1).
Пусть
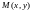 – любая точка эллипса,
– любая точка эллипса,
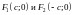 – фокусы. Тогда по определению имеем
– фокусы. Тогда по определению имеем
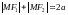 ,
где
,
где
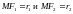 называются фокальными
радиусами, и, следовательно,
называются фокальными
радиусами, и, следовательно,
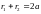 .
.
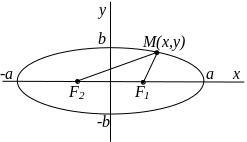
Рис. 9.1
Форма
эллипса (мера его сжатия) характеризуется
его эксцентриситетом
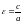 ,
(так как с
< а,
то
< 1 для эллипса). Каноническое
уравнение эллипса
:
,
(так как с
< а,
то
< 1 для эллипса). Каноническое
уравнение эллипса
:
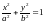 ,
причем
,
причем
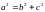 .
Здесь a
– большая,
.
Здесь a
– большая,
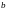 –
малая полуоси эллипса. Если а
=
(с
= 0,
= 0, фокусы сливаются в одной точке –
центре), то эллипс превращается в
окружность
–
малая полуоси эллипса. Если а
=
(с
= 0,
= 0, фокусы сливаются в одной точке –
центре), то эллипс превращается в
окружность
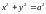 .
Фокальные радиусы эллипса:
.
Фокальные радиусы эллипса:
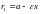 (правый фокальный радиус) и
(правый фокальный радиус) и
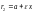 (левый
фокальный радиус).
(левый
фокальный радиус).
3 .Гипербола
– это множество точек плоскости,
абсолютная величина разности расстояний
которых до двух данных точек, называемых
фокусами, есть величина постоянная,
равная 2а, причем эта постоянная
меньше расстояния между фокусами
(рис.9.2). Пусть
–
любая точка гиперболы,
.Гипербола
– это множество точек плоскости,
абсолютная величина разности расстояний
которых до двух данных точек, называемых
фокусами, есть величина постоянная,
равная 2а, причем эта постоянная
меньше расстояния между фокусами
(рис.9.2). Пусть
–
любая точка гиперболы,
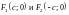 –
фокусы. Тогда по определению имеем
–
фокусы. Тогда по определению имеем
Рис. 9.2
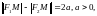 где
где
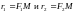 называются фокальными
радиусами,
причем для
правой ветви гиперболы,
называются фокальными
радиусами,
причем для
правой ветви гиперболы,
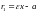 – правый фокальный радиус;
– правый фокальный радиус;
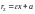 – левый фокальный радиус, где число
– левый фокальный радиус, где число
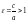 называется эксцентриситетом
гиперболы. Каноническое уравнение
гиперболы имеет
вид
называется эксцентриситетом
гиперболы. Каноническое уравнение
гиперболы имеет
вид
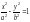 ,
где
,
где
а2
+ в2
= с2.
Здесь а
– действительная полуось,
b
– мнимая
полуось гиперболы; из уравнения видно,
что гипербола не пересекает ось OY,
т.е.
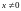 .
Для построения
гиперболы строят прямоугольник со
сторонами 2а
и 2b,
с центром в начале координат. Проводят
диагонали в прямоугольнике, которые
являются асимптотами
.
Для построения
гиперболы строят прямоугольник со
сторонами 2а
и 2b,
с центром в начале координат. Проводят
диагонали в прямоугольнике, которые
являются асимптотами
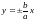 .
Вершины гиперболы находятся в точках
.
Вершины гиперболы находятся в точках
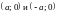 .
.
Замечание.
Если
уравнение гиперболы имеет вид :
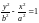 ,
то вершины гиперболы находятся на оси
OY
в точках
,
то вершины гиперболы находятся на оси
OY
в точках
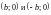 .
Гиперболы
называются сопряженными
(у
них действительная ось одной гиперболы
служит мнимой осью другой, и наоборот;
они имеют общие асимптоты).
Если а=
b,
то уравнение принимает вид х2
–
у2
=
а2.
Такая гипербола называется равнобочной.
Ее
асимптоты перпендикулярны друг к другу.
Поэтому, если за координатные оси принять
асимптоты равнобочной гиперболы, то ее
уравнение примет вид:
.
Гиперболы
называются сопряженными
(у
них действительная ось одной гиперболы
служит мнимой осью другой, и наоборот;
они имеют общие асимптоты).
Если а=
b,
то уравнение принимает вид х2
–
у2
=
а2.
Такая гипербола называется равнобочной.
Ее
асимптоты перпендикулярны друг к другу.
Поэтому, если за координатные оси принять
асимптоты равнобочной гиперболы, то ее
уравнение примет вид:
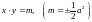 (рис. 9.3,а и рис. 9.3,б), или
(рис. 9.3,а и рис. 9.3,б), или
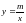 .
.
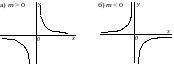
Рис. 9.3
4. Парабола – это
множество точек плоскости, равноудаленных
от данной точки, называемой фокусом, и
от данной прямой, называемой директрисой
(рис.9.4). Пусть прямая l:
x=-p/2
является директрисой параболы, точка
F(p/2,0)
– фокус. Тогда каноническое уравнение
параболы имеет вид:
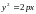 ,
,
где
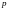 –
фокальный параметр.
–
фокальный параметр.
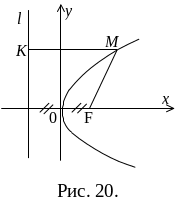
Рис. 9.4
Эта
парабола расположена симметрично
относительно оси ОХ
(
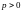 ),
),
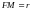 – фокальный радиус параболы, который
определяется по формуле
– фокальный радиус параболы, который
определяется по формуле
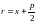 ,
так как
,
так как
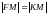 .
Уравнение
.
Уравнение
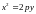 является уравнением параболы, симметричной
относительно оси ординат ОУ.
При р
> 0 ветви параболы направлены в
положительную сторону соответствующей
координатной оси, а при р < 0 – в
отрицательную сторону.
является уравнением параболы, симметричной
относительно оси ординат ОУ.
При р
> 0 ветви параболы направлены в
положительную сторону соответствующей
координатной оси, а при р < 0 – в
отрицательную сторону.
