
- •Введение
- •Определители, матрицы. Системы линейных уравнений
- •2. Линейные пространства.
- •Решение систем линейных уравнений
- •3. Подпространства, образованные решениями линейной однородной системы (лос) уравнений. Нахождение общего решения лос
- •4. Линейные преобразования и действия Над ними
- •5. Собственные значения и собственые векторы матрицы
- •6. Приведение квадратичной формы к каноническому виду
- •7. Векторы и действия над ними
- •8. Плоскость и прямая в пространстве
- •9. Кривые второго порядка на плоскости
- •10. Приведение общего уравнения кривой второго порядка к каноническому виду
- •11. Исследование общего уравнения кривой. Поверхности второго порядка.
- •12. Комплексные числа. Теорема
- •И ее предел.
- •13. Функция. Предел функции
- •14. Применение эквивалентных бесконечно малых к вычислению пределов
- •15. Производная функции и ее вычисление
- •16. Дифференциал функции. Применение дифференциала
- •17. Неопределенный интеграл
- •18. Определенный интеграл
- •19. Несобственные интегралы
- •20. Приложения определённого интеграла
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •21. Функции нескольких переменных Основные теоретические сведения
- •22. Частные производные первого порядка. Полный дифференциал функции и его применение к приближенным вычислениям
- •1) Случай одной независимой переменной.
- •23. Производные и дифференциалы высших порядков
- •1) Случай одной независимой переменной.
- •2) Случай нескольких независимых переменных.
- •24. Формула Тейлора для функции двух переменных
- •25. Экстремум функции нескольких независимых переменных
- •26. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •27. Дифференциальные уравнения
- •28. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •29. ЧиСлоВые ряды
- •30. Функциональные ряды
- •31. Тригонометрические ряды Фурье
- •32. Интеграл Фурье
- •33. Двойной интеграл
- •34. Тройные интегралы
- •35. Криволинейные интегралы
- •36. Поверхностные интегралы
- •Поверхностные интегралы второго рода
- •Так же получены формулы:
- •37. Теория поля
- •Скалярные поля
- •Формула Остроградского на плоскости
- •Циркуляция вектора вдоль контура не зависит от выбора координатной системы.
- •38. Оператор Гамильтона
- •Дифференциальные операции второго порядка
- •39. Функция комплексного переменного
- •40. Дифференцирование функций комплексного переменного, условия коши — римана
- •41. Интегрирование функций комплексного переменного
- •42. Ряд лорана
- •43. Преобразование Лапласа
- •44. Задача коши для обыкновенных линейных дифференциальных уравнений
- •Заключение
- •Библиографический список
- •35. Криволинейные интегралы ……………………………….302
- •394026 Воронеж, Московский просп.,14
15. Производная функции и ее вычисление
Если
х и
х1
– значения
аргумента х,
а y=f(x)
и y=f(x1)
- соответственно значения функции y=f(x)
,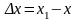 то называется приращением
аргумента х
на отрезке
[x;
х1],
а
то называется приращением
аргумента х
на отрезке
[x;
х1],
а
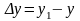 (или
=
(или
=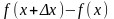 )
называется приращением функции на том
же отрезке [x;
х1],
)
называется приращением функции на том
же отрезке [x;
х1],
(см.
рис. 15.1),
где
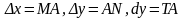 ).
).
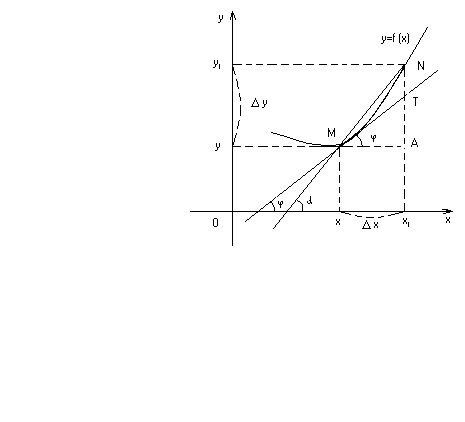
Рис.15.1
Отношение
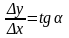 называется средней скоростью
изменения
функции y=f(x)
на отрезке
называется средней скоростью
изменения
функции y=f(x)
на отрезке
 .
.
Производной
функции
y=f(x)
в точке x
называется предел отношения приращения
функции
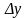 к приращению аргумента
к приращению аргумента
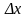 , когда приращение аргумента стремится
к нулю:
, когда приращение аргумента стремится
к нулю:
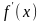 =
=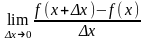 ,
если этот предел существует.
,
если этот предел существует.
Геометрический
смысл производной:
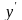 =tg
-
угловой коэффициент касательной МТ
к графику функции y=f(x)
в точке х
(рис. 15.1).
=tg
-
угловой коэффициент касательной МТ
к графику функции y=f(x)
в точке х
(рис. 15.1).
Физический
смысл производной
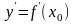 -
мгновенная скорость, т.е. скорость
изменения функции в данный момент х0.
Таким образом, быстрота протекания
физических, химических и других процессов
выражается с помощью производной.
Функция, имеющая конечную производную,
называется дифференцируемой.
Операция
нахождения производной называется
дифференцированием.
-
мгновенная скорость, т.е. скорость
изменения функции в данный момент х0.
Таким образом, быстрота протекания
физических, химических и других процессов
выражается с помощью производной.
Функция, имеющая конечную производную,
называется дифференцируемой.
Операция
нахождения производной называется
дифференцированием.
Основные правила дифференцирования.
Если
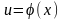 ,
,
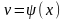 - функции, имеющие производные, c-
постоянная величина, то:
- функции, имеющие производные, c-
постоянная величина, то:
1)
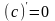 (c=const); 2)
(c=const); 2)
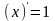 ; 3)
; 3)
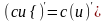 ;
;
4)
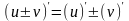 ;
5)
;
5)
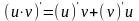 ;
;
6)
; 7)
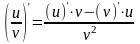 .
.
Производная сложной функции.
Таблица производных
Если
 и
- дифференцируемые функции своих
аргументов, то производная сложной
функции
и
- дифференцируемые функции своих
аргументов, то производная сложной
функции
 существует и равна произведению
производной данной функции y
по промежуточному аргументу u
на производную промежуточного аргумента
u
по независимой переменной х:
существует и равна произведению
производной данной функции y
по промежуточному аргументу u
на производную промежуточного аргумента
u
по независимой переменной х:
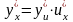 ,
или
,
или
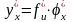 ,
или
,
или
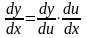 .
Это правило распространяется на
из любого
конечного числа дифференцируемых
функций.
.
Это правило распространяется на
из любого
конечного числа дифференцируемых
функций.
Таблица производных основных
элементарных функций.
Пусть
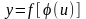 ,
где
,
где
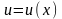 .
Тогда:
.
Тогда:
1)
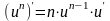 ( n
- любое число);
( n
- любое число);
2)
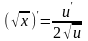 ;
3)
;
3)
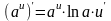 (a>0,
(a>0,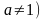 ;
;
4)
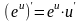 ;
5)
;
5)
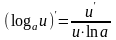 ;
;
6)
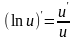 ;
7)
;
7)
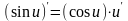 ;
;
8)
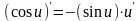 ;
9)
;
9)
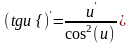 ;
;
10)
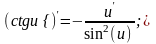 11)
11)
 ,(
,(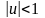 );
);
12)
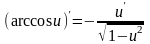 ,
(
);
13)
,
(
);
13)
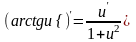 ;
;
14)
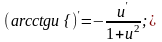 15)
15)
 ;
;
16)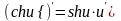 ;
17)
;
17)
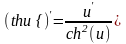 ;
18)
;
18)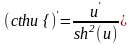 .
.
Замечание. Гиперболические функции определены так:
1)
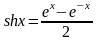 -
гиперболический синус
-
гиперболический синус
2)
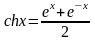 -гиперболический
косинус
-гиперболический
косинус
3)
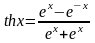 -гиперболический
тангенс
-гиперболический
тангенс
4) -гиперболический котангенс
Для гиперболический функций имеют место формулы, аналогичные фомулам для тригонометрических функций.
Основные формулы:
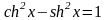 ;
;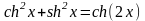 ;
;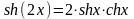 ;
;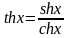 ,
,
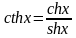 ;
и т.д.
;
и т.д.
Пример 1. Найти , если =sin3(x/4).
Решение. Это сложная функция промежуточным первым аргументом u= sin(x/4) и t=x/4 . Данную функцию можно представить в виде: y=u3 , где u=sin(t); t=x/4 .
Дифференцируя, получаем:
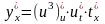 =
=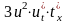 =
=
=
=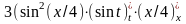 =
=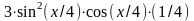 .
.
Уравнение касательной и нормали к плоской кривой
Пусть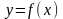 -
уравнение плоской кривой,
-
уравнение плоской кривой,
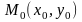 -
точка, лежащая на этой кривой, так что
-
точка, лежащая на этой кривой, так что
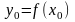 .
.
Уравнение
касательной
к данной кривой
,
проходящей через точку касания
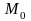 кривой, имеет вид:
кривой, имеет вид:
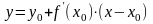 ,
,
где
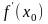 есть угловой коэффициент касательной
к данной кривой, проходящей через точку
.
Иначе говоря, где
есть угловой коэффициент касательной
к данной кривой, проходящей через точку
.
Иначе говоря, где
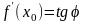 ,
- угол между касательной к кривой ,
проведенный через точку
,
и промежуточным направлением оси абсцисс
.
,
- угол между касательной к кривой ,
проведенный через точку
,
и промежуточным направлением оси абсцисс
.
Нормалью
к кривой в
точке
называется перпендикуляр к касательной,
проведенный через точку касания.
Уравнение нормали к кривой
в точке
имеет вид:
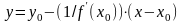 .
.
Пример 2 . Составить уравнение касательной и нормали к кривой y=x3+2x в точке с абсциссой x0=1.
Решение.
Найдем производную данной функции и
ее значение при x0=1,
y
/=3x2+2,
y
/(x0)=y
/(1)=3+2=5.
Угловой коэффициент касательной
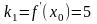 .
Вычислим значение функции при x0=1:
.
Вычислим значение функции при x0=1: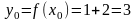 .
Следовательно,
.
Следовательно,
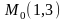 -точка
касания и уравнение касательной будет
y=3+5(x-1),
или 5x-y-2=0;
а уравнение нормали y=3-(1/5)(x--1),
или x+5y-16=0
, где угловой коэффициент нормали
k2=-1/k1,
так как условием перпендикулярности
двух прямых y=k1x+b1
и y=k2
x+b2
является соотношение:k1
k
2
=-1 Ответ:
5x-y-2=0,
x+5y-16=0
.
-точка
касания и уравнение касательной будет
y=3+5(x-1),
или 5x-y-2=0;
а уравнение нормали y=3-(1/5)(x--1),
или x+5y-16=0
, где угловой коэффициент нормали
k2=-1/k1,
так как условием перпендикулярности
двух прямых y=k1x+b1
и y=k2
x+b2
является соотношение:k1
k
2
=-1 Ответ:
5x-y-2=0,
x+5y-16=0
.
