36. Поверхностные интегралы

Поверхностные интегралы первого рода

Определение поверхностного интеграла

от скалярной функции.

Пусть в точках кусочно-гладкой поверхности Σ с кусочно-гладкой границей C определена некоторая ограниченная функция f(M). Разобьем поверхность Σ кусочно-гладкими кривыми на части Σ₁, ..., Σ_n (рис. 36.1). Площадь каждой из них обозначим Ds _i (i=1,…,n). Пусть в каждой из этих площадей выбрана произвольная точка M_i . Составим сумму

T=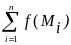 Ds _i. (36.1)

Величина Т будет называться интегральной суммой отвечающей функции f(M) (при данном разбиении поверхности Σ и выборе точек M). Поверхность Σ может быть, в частности, замкнутой.

Определение. Если при стремлении наибольшего из диаметров частей Σ_k, поверхности Σ к нулю интегральные суммы Т стремятся к некоторому конечному пределу, то этот предел называется поверхностным интегралом первого рода от функции f (M) по поверхности Σ и обозначается символом 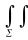f(M) ds.

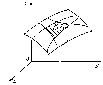
Рис.36.1

Точку M поверхности Σ можно задать декартовыми координатами x, у, z Поэтому функцию f (М), определенную на Σ, мы будем обозначать также f(x, у, z), а соответствующий поверхностный интеграл - f(x, у, z) ds. Приведем поверхностный интеграл к двойному интегралу. Рассмотрим сначала простейший случай, когда поверхность задана уравнением в декартовых координатах.

Пусть Σ - гладкая поверхность, заданная уравнением

z = z(x, y), (x, y)є D , где D—замкнутая ограниченная область, a f(x, y, z)-некоторая ограниченная функция, определенная на поверхности Σ. Тогда справедливо равенство

f(x, y, z) ds = f(x, y, z(x ,y)) 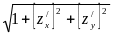dxdy . (36.2)

При этом поверхностный интеграл, стоящий слева, существует, если существует двойной интеграл, стоящий в правой части равенства.

Рис. 36.2

Доказательство. Разобьем поверхность Σ кусочно - гладкими кривыми на п частей Σ_i (i=1,…n). Проекции разбиений Σ_i на плоскость х0у обозначим D_i (рис. 36.2). При этом диаметр каждого из элементов D_i, будет не больше,

чем диаметр соответствующего элемента Σ_i, поверхности Σ.

Рассмотрим сумму T=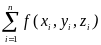 Δs_i .

Площадь Δs_i элемента Σ_i вычисляем по формуле Δs_i = 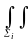dxdy,

где z= z(x, y), и по теореме о среднем для двойного интеграла от непрерывной функции имеем

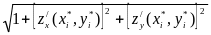Δs_i = S_i,

где (х_i*, у_i^*)- некоторая точка, принадлежащая области D_i, а S _i-площадь этой области. Интегральную сумму T можно записать

так

T= 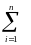f( x_i ,y_i ,z(x_i ,y_i )) S_i (36.3)

Сравним ее с интегральной суммой вида

T^*= f(x_i, y_i, z(x_i, y_i)) 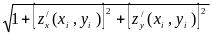S_i . (36.4)

Выражение T* отвечает двойному интегралу, стоящему в равенстве (36.2) справа при том разбиении области D , которое соответствует данному разбиению поверхности Σ. T , T* отличаются друг от друга только тем, что в сумме (36.4) значения функции f и под квадратным корнем берутся в точке (х_i, у_i) (произвольно выбираемой внутри элемента D _i), а в (36.4) значения под квадратным корнем берутся в точке

( x_i^*, y_i^*), диктуемой нам теоремой о среднем. Эти суммы равны. Предел интегральных сумм Т существует и равен интегралу, стоящему в (36.2) справа.

Следствие. Если поверхность Σ гладкая, а функция f(x, у, z) непрерывна на ней, то интеграл f(x, у, z) ds существует.

Действительно, в этом случае в равенстве (36.2) справа стоит интеграл от непрерывной функции. Он существует, следовательно, существует и стоящий слева поверхностный интеграл.

Замечание. Пусть поверхность Σ состоит из нескольких частей, каждая из которых может быть представлена уравнением вида x= x(y, z), y= y(z, х) или z= z(x, y). Для сведения поверхностного интеграла, взятого по такой поверхности к двойному интегралу можно, воспользоваться тем, что поверхностный интеграл по поверхности Σ равен сумме интегралов, взятых по составляющим эту поверхность частям. Легко проверить, что эти формулы остаются в силе, когда поверхность не гладкая, а кусочно-гладкая.

Пример 1 . Вычислить поверхностный итеграл

J = (x²+ y²)^1.5ds, – часть поверхности z²= x²+ y², заключенной между плоскостями z = 0, z = 1.

Решение. Вычислим

, , ds = =

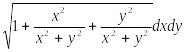= = . Тогда интеграл J можно

преобразовать в двойной и вычислить с помощью полярной системы координат (x = r cos φ , y = r sin φ, 0≤ r ≤1, 0≤ φ≤ π/2)

J = (x² + y²)^1.5 =4 =2π /5.

где – D проекция поверхности Σ на плоскость XOY

(D: x² + y² ≤ 1).

Применения поверхностных интегралов механике

Поверхностные интегралы первого рода часто встречаются в физических задачах. С такими интегралами приходится иметь дело при изучении распределения масс по поверхности, например при нахождении координат центра масс, моментов инерции материальных поверхностей.

Пусть по поверхности Σ (гладкой или кусочно-гладкой) распределена некоторая масса с поверхностной плотностью ρ(х, у, z), представляющей собой непрерывную функцию на Σ. Такую поверхность Σ будем кратко называть материальной поверхностью. Тогда имеют место следующие формулы:

1. Масса μ материальной поверхности Σ равна

μ= ρ(х, у, z)ds.

2) Координаты центра масс материальной поверхности определяются формулами x_c = (1/S) xρ(х, у, z) ds ,

y_c = (1/S) yρ(x, y, z) ds , z_c = (1/S) zρ(x, y, z) ds,

S = ρ(x, y,z)ds. (36.5)

Для однородной поверхности ρ= const .

2. Моменты инерции поверхности Σ относительно осей координат равны

J_z= (x² + y²) ρ(x, y, z) ds, J_y= (x² + z²) ρ(x, y, z) ds,

J_x= (z² + y²) ρ(x, y, z) ds.

Пример 2. Вычислить площадь поверхности (S) части пароболоида y=x²+z² в первом октанте, ограниченной плоскостью y=2.

Решение. Введем полярную систему координат x = r cos φ ,

z = r sin φ, 0≤ r ≤ , тогда

S = dxdz = dxdz=

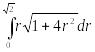=– = (1+4r²)^3/2 = .

Поверхностные интегралы от векторных функций.

Выше были рассмотрены поверхностные интегралы от скалярных функций. Это понятие можно перенести на векторные функции. Пусть (M) = P i + Q j + R k - некоторая векторная функция, заданная на поверхности Σ. Определим интеграл от этой функции по поверхности Σ, положив

(M) ds = i P(M) ds + j Q(M) ds + k R(M) ds.

Существуют задачи, в которых ориентация элемента ds играет существенную роль. К ним относится задача о расчете количества жидкости, протекающей через поверхность за единицу времени, а также и ряд других. Эти задачи приводит к другому понятию поверхностного интеграла, так называемому поверхностному интегралу второго рода.