- •Введение
- •Определители, матрицы. Системы линейных уравнений
- •2. Линейные пространства.
- •Решение систем линейных уравнений
- •3. Подпространства, образованные решениями линейной однородной системы (лос) уравнений. Нахождение общего решения лос
- •4. Линейные преобразования и действия Над ними
- •5. Собственные значения и собственые векторы матрицы
- •6. Приведение квадратичной формы к каноническому виду
- •7. Векторы и действия над ними
- •8. Плоскость и прямая в пространстве
- •9. Кривые второго порядка на плоскости
- •10. Приведение общего уравнения кривой второго порядка к каноническому виду
- •11. Исследование общего уравнения кривой. Поверхности второго порядка.
- •12. Комплексные числа. Теорема
- •И ее предел.
- •13. Функция. Предел функции
- •14. Применение эквивалентных бесконечно малых к вычислению пределов
- •15. Производная функции и ее вычисление
- •16. Дифференциал функции. Применение дифференциала
- •17. Неопределенный интеграл
- •18. Определенный интеграл
- •19. Несобственные интегралы
- •20. Приложения определённого интеграла
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •21. Функции нескольких переменных Основные теоретические сведения
- •22. Частные производные первого порядка. Полный дифференциал функции и его применение к приближенным вычислениям
- •1) Случай одной независимой переменной.
- •23. Производные и дифференциалы высших порядков
- •1) Случай одной независимой переменной.
- •2) Случай нескольких независимых переменных.
- •24. Формула Тейлора для функции двух переменных
- •25. Экстремум функции нескольких независимых переменных
- •26. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •27. Дифференциальные уравнения
- •28. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •29. ЧиСлоВые ряды
- •30. Функциональные ряды
- •31. Тригонометрические ряды Фурье
- •32. Интеграл Фурье
- •33. Двойной интеграл
- •34. Тройные интегралы
- •35. Криволинейные интегралы
- •36. Поверхностные интегралы
- •Поверхностные интегралы второго рода
- •Так же получены формулы:
- •37. Теория поля
- •Скалярные поля
- •Формула Остроградского на плоскости
- •Циркуляция вектора вдоль контура не зависит от выбора координатной системы.
- •38. Оператор Гамильтона
- •Дифференциальные операции второго порядка
- •39. Функция комплексного переменного
- •40. Дифференцирование функций комплексного переменного, условия коши — римана
- •41. Интегрирование функций комплексного переменного
- •42. Ряд лорана
- •43. Преобразование Лапласа
- •44. Задача коши для обыкновенных линейных дифференциальных уравнений
- •Заключение
- •Библиографический список
- •35. Криволинейные интегралы ……………………………….302
- •394026 Воронеж, Московский просп.,14
42. Ряд лорана
Функция
,
однозначная н аналитическая в кольце![]() разлагается в этом кольце в
ряд Лорана
разлагается в этом кольце в
ряд Лорана
![]() (42.1)
(42.1)
коэффициенты находятся по формулам
![]() (42.2)
(42.2)
Здесь
Г—произвольная окружность с центром
в точке
,
лежащая
внутри заданного кольца. Разложение в
ряд Лорана единственно. В формуле (42.1)
ряды
![]()
называются соответственно гласной частью ряда Лорана и
правильной
частью ряда Лорана.
На практике для нахождения коэффициентов
![]() ,
если это возможно, используют готовые
разложения элементарных функций в ряд
Тейлора. Для примера разложим в ряд
Лорана с центром в точке
,
если это возможно, используют готовые
разложения элементарных функций в ряд
Тейлора. Для примера разложим в ряд
Лорана с центром в точке
![]() функцию
функцию
![]() Функция
Функция
![]() аналитична
в кольце 0 < | z
| < ∞, следовательно, разложима в нем
в ряд Лорана. Воспользуемся разложением
показательной функции в ряд Тейлора в
окрестности точки
аналитична
в кольце 0 < | z
| < ∞, следовательно, разложима в нем
в ряд Лорана. Воспользуемся разложением
показательной функции в ряд Тейлора в
окрестности точки
![]()
![]() и положим
и положим
![]() тогда
тогда
![]()
![]()
В
силу единственности ряда Лорана
полученное разложение функции f(z)
по степеням z
является
рядом Лорана для функции
![]() в
кольце 0 < | z
| < ∞.
в
кольце 0 < | z
| < ∞.
Пример
1 . Найти
все Лорановские разложения данной
функции по степеням z.
![]()
Решение:
![]()
Представим один из множителей, как сумму двух простых слагаемых:
![]()
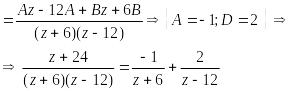 .Отсюда
f(z)
примет вид: f(z)=
.Отсюда
f(z)
примет вид: f(z)=
![]() .
Особые точки: z
= 0; z
= -6; z
= 12
.
Особые точки: z
= 0; z
= -6; z
= 12
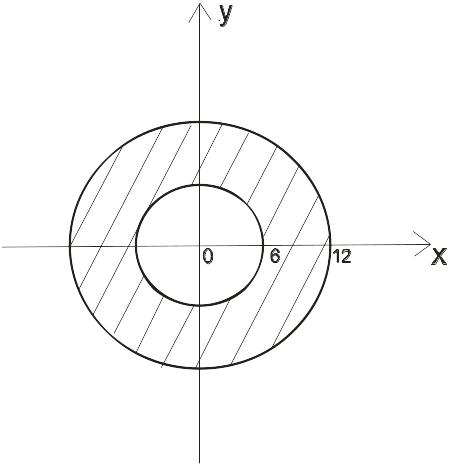
Рис. 42.1
Рассмотрим
область
![]()
![]() =
=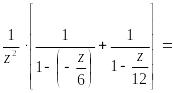
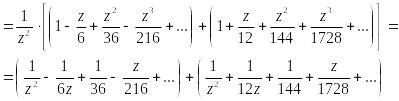
Рассмотрим
область
![]()
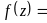 =
=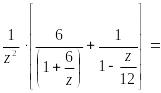
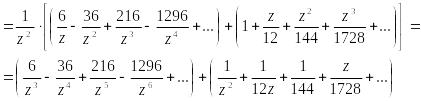
Рассмотрим
область
![]() =
=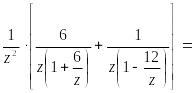
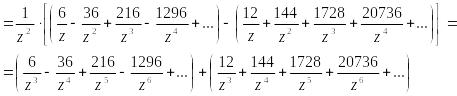
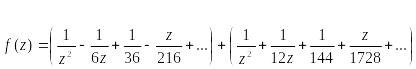
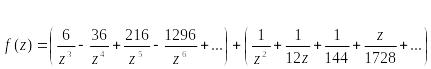
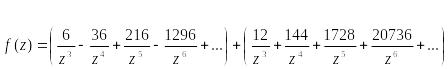
Изолированные особые точки однозначной
аналитической функции
Точка
называется
изолированной особой точкой функции
,
если
f
(z)-
однозначная и аналитическая функция в
круговом кольце![]() кроме
самой точки
.
Функцию
в
окрестности
точки
можно
разложить в
ряд
Лорана(6), сходящийся в
кольце
кроме
самой точки
.
Функцию
в
окрестности
точки
можно
разложить в
ряд
Лорана(6), сходящийся в
кольце
![]() .
.
При этом возможны три различных случая, когда ряд Лорана:
не содержит членов с отрицательными степенями
разности![]() В этом случае
называется
устранимой
особой
точкой функции
;
В этом случае
называется
устранимой
особой
точкой функции
;
содержит конечное число членов с отрицательными степенями разности
![]() .
.
В этом случае называется полюсом порядка n функции ;
3) содержит бесконечное число членов с отрицательными степенями разности
![]() .
.
В этом случае называется существенно особой точкой функции . При определении характера изолированной особой точки используются следующие утверждения.
1. Для того чтобы точка являлась устранимой особой
точкой
аналитической функции
,
необходимо и достаточно существование
предела
![]()
Для того чтобы точка являлась полюсом аналитической
функции , необходимо и достаточно существование
предела
![]()
2.
Для того чтобы точка
являлась
полюсом порядка п
аналитической
функции
f(z),
необходимо
и
достаточно,
чтобы функцию
f(z)
можно
было
представить в виде
![]() —функция
аналитическая в точке
,
причем
—функция
аналитическая в точке
,
причем
![]() .
.Пусть
—изолированная
особая точка функции
.
.Пусть
—изолированная
особая точка функции
![]() —функции аналитические в точке
.
Если числитель
—функции аналитические в точке
.
Если числитель
![]() и
все
производные
до
к—1
порядка
включительно
в точке
равны нулю,
и
все
производные
до
к—1
порядка
включительно
в точке
равны нулю,
![]() знаменатель
знаменатель
![]() и
все производные
до
l-1
порядка включительно также равны нулю
в точке
,
и
все производные
до
l-1
порядка включительно также равны нулю
в точке
,![]() то
при l>k
точка
является
полюсом порядка n=l—k
аналитической
функции f(z).
(Если
то
при l>k
точка
является
полюсом порядка n=l—k
аналитической
функции f(z).
(Если
![]() то
точка
является устранимой особой
точкой
аналитической функции f(z).)
В
частном случае, при k=0,
l
= 1
имеем: если
то
точка
является устранимой особой
точкой
аналитической функции f(z).)
В
частном случае, при k=0,
l
= 1
имеем: если
![]() —
полюс первого порядка функции f(z).
—
полюс первого порядка функции f(z).
3.
Пусть при
![]() аналитическая функция
не
имеет пределов ни конечного, ни
бесконечного. Это условие является
необходимым и достаточным для того,
чтобы точка
была
существенно особой точкой функции
.
аналитическая функция
не
имеет пределов ни конечного, ни
бесконечного. Это условие является
необходимым и достаточным для того,
чтобы точка
была
существенно особой точкой функции
.
Пример 2 . Для данной функции найти изолированные особые точки и определить их тип.
f
(z)
=
![]() .
.
Решение: Изолированными особыми точками являются z = i,
z
= -i,
z
= ½, z
= - ½. Запишем данную функцию в виде
отношения g
(z)
и h
(z):
f
(z)
=
![]() ;g
(z)
= cos
πz;
;g
(z)
= cos
πz;
h (z) = (4z 2 -1)(z 2 + 1). Для каждой из функций найдём порядок производной, не обращающейся в ноль при z = i, z = -i, z = ½, z = - ½: g (1/2) = 0, g (-1/2) = 0, g (i) ≠ 0, g (-i) ≠ 0;
g׳(z) = - π sin πz, g ׳ (1/2) ≠ 0, g ׳ (-1/2) ≠ 0; h (1/2) = 0,
h (-1/2) = 0, h (i) = 0, h (-i) = 0; h ׳ (z) = 16z 3 + 6z;
h ׳ (1/2) ≠ 0, h ׳ (-1/2) ≠ 0, h ׳ (i) ≠ 0, h ׳ (-i) ≠ 0.
При z = ½ и z = - ½ порядок ненулевой производной для функции, стоящей в знаменателе, равен порядку ненулевой
производной для функции, стоящей в числителе. Таким образом, можно сделать вывод, что z = ½ и z = - ½ являются
устранимыми особыми точками. Так как порядок производной, не обращающейся в ноль при z = i и z = -i выше для функции, находящейся в знаменателе, то точки z = i и z = -i являются полюсами функции. Порядок этих полюсов находится, как разница между порядками производных, не обращающихся в ноль. В данном случае, это 1 – 0 = 1. Точки z = ½ и z = - ½ являются устранимыми особыми точками. Точки z = i и z = -i являются полюсами 1-го порядка.
Вычеты
Пусть
— изолированная особая точка функции
.
Вычетом
функции f
(z)
в точке
называется
число, обозначаемое символом
![]() и определяемое равенством
и определяемое равенством
![]() (42.3)
(42.3)
(другие
обозначения:![]() ).
Замкнутый контур интегрирования γ лежит
в области аналитичности функции f
(z)
и не содержит внутри других особых
точек функции f
(z),
кроме
.
Сопоставление формул (42.1) и (42.3) показывает,
что вычет функции равен коэффициенту
при минус первой степени в лорановском
разложении f
(z)
в окрестности точки
:
).
Замкнутый контур интегрирования γ лежит
в области аналитичности функции f
(z)
и не содержит внутри других особых
точек функции f
(z),
кроме
.
Сопоставление формул (42.1) и (42.3) показывает,
что вычет функции равен коэффициенту
при минус первой степени в лорановском
разложении f
(z)
в окрестности точки
:
![]() .
(42.4)
.
(42.4)
Вычет в устранимой особой точке равен нулю. Вычет функции f (z) в полюсе n-гo порядка вычисляется по формуле
![]()
при n=1
![]()
Если
функция
в окрестности точки
представляется как частное двух
аналитических функций,
![]() причем
причем
![]()
![]() (в этом случае
—
полюс первого порядка функции f
(z)),
то
(в этом случае
—
полюс первого порядка функции f
(z)),
то
![]()
Если точка есть существенно особая точка функции
, то вычет вычисляется по формуле (42.4).
Основная теорема Коши о вычетах.
Если
функция
является
аналитической на границе Г
области
G
и всюду внутри области, за исключением
конечного числа особых точек
![]() ,
то
,
то
![]() (42.5)
(42.5)
Пример 3. Вычислить интеграл:
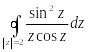
Решение: Найдем особые точки функции f(z):
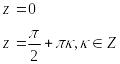
В
рассматриваемую область попадают точки
![]() Точка
Точка
![]() является
простым нулем.
является
простым нулем.
Найдем вычет в этой точке:
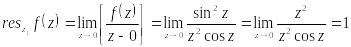
Точка
![]() является простым полюсом. Найдем вычет
в этой точке:
является простым полюсом. Найдем вычет
в этой точке:
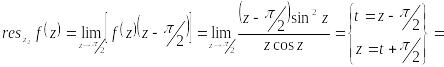
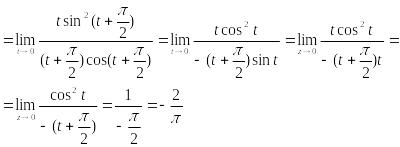
Точка
![]() является простым полюсом. Найдем
является простым полюсом. Найдем
вычет в этой точке:

Отсюда следующий результат:
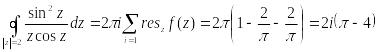
Вычисление несобственных интегралов от
рациональных функций
Пусть
R
(x)
— рациональная функция,
![]() где
где
![]() и
и
![]() -
многочлены степеней
-
многочлены степеней
k
и
l
соответственно. Если R
(х)
непрерывна
на всей действительной оси и
![]() ,
т.е. степень знаменателя, по крайней
мере, на две единицы больше степени
числителя, то
,
т.е. степень знаменателя, по крайней
мере, на две единицы больше степени
числителя, то
![]() здесь
сумма вычетов функции
здесь
сумма вычетов функции
![]() берется
по всем полюсам
берется
по всем полюсам
![]() ,
расположенным в верхней полуплоскости
Im
z>0.
,
расположенным в верхней полуплоскости
Im
z>0.
Вычисление несобственных интегралов специального вида
Пусть
R
(x)
— рациональная функция,
где
и
-
многочлены степеней k
и
l
соответственно. Если R
(х)
непрерывна
на всей действительной оси и
![]() (т. е. R(x)
– правильная рациональная дробь), то
(т. е. R(x)
– правильная рациональная дробь), то
![]()
![]()
где
сумма вычетов функции
![]() берется по всем полюсам
,
расположенным в верхней полуплоскости
Im
z>0.
берется по всем полюсам
,
расположенным в верхней полуплоскости
Im
z>0.
Пример
4 .
Вычислить
интеграл:![]()
Решение: Известно, что если функция рациональная, а ее числитель и знаменатель представляют собой многочлены, причем степень знаменателя, по крайней мере, на две единицы больше степени числителя, то можно применить следующую формулу:
![]() .
Сумма вычетов берется по всем полюсам
полуплоскости
.
Сумма вычетов берется по всем полюсам
полуплоскости
![]()
Преобразуем исходный материал:
![]()
Особые точки:
![]()
![]()
![]()
![]()
![]()
![]()
Точки и являются простыми полюсами и вычеты в них вычисляются следующим образом:
![]()
![]() и
и
используем приведенную в начале задачи формулу:
![]() .
.
Пример 5. Вычислить интеграл:
![]()
Решение: Для вычисления интегралов такого вида применяется специальная формула:
![]()
Исходная функция полностью удовлетворяет условиям
применения
данной формулы. Найдем
:![]()
Сумма
вычетов берется по верхней полуплоскости
.
Из этого следует:
![]()
Эта особая точка является полюсом второго порядка. Найдем в ней вычет для каждой из функций:
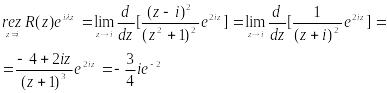
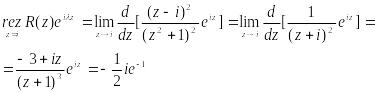
Используем записанную ранее формулу и найдем интеграл:
![]()
Вычисление определенных интегралов
специального вида
Пусть
R
—рациональная функция cos
t
и
sin
t,
непрерывная внутри промежутка
интегрирования. Полагаем
![]() ,
тогда
,
тогда
![]()
имеем
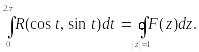 (42.6)
(42.6)
где путь интегрирования—окружность единичного радиуса с
центром в начале координат. Контурный интеграл в правой
части равенства (42.6) вычисляется по формуле (42.5), где сумма вычетов функции F(z) берется по всем особым точкам, лежащим в области | z|< 1.
Пример 6 . Вычислить интеграл:
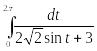
Решение: Интеграл такого вида может быть преобразован в контурный, используя следующие выражения:
![]()
![]()
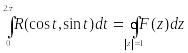
Воспользуемся этими данными и получим:
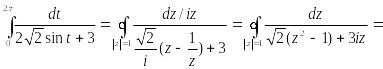
=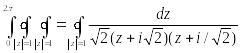
Подынтегральная функция имеет две особые точки:
![]() Точка
Точка
![]() не попадает в область,
не попадает в область,
ограниченную
контуром интегрирования. Точка
![]()
является простыми полюсом. Вычислим в этой точке вычет:
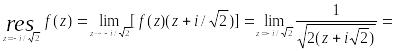
![]() .
По основной теореме Коши о вычетах:
.
По основной теореме Коши о вычетах: