7. Векторы и действия над ними
Вектор
– это направленный отрезок, т.е. имеющий
длину и направление. Длина вектора
называется модулем и обозначается
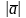или
.
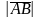Векторы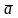
,
-
коллинеарны (
//
)
, если параллельны одной и той же прямой
или лежат на одной прямой.
Векторы
,
,
–
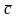компланарны, если они параллельны одной
и той же плоскости или лежат в одной и
той же плоскости.
Направление вектора определяется углами α, β, γ, образованными вектором с положительным направлением координатных осей OX , OY , OZ соответственно.
Направляющие
косинусы вектора вычисляются по формулам:
,
,
,
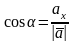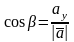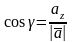где
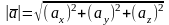, если известны его координаты
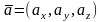. Заметим, что направляющие косинусы
являются координатами любого единичного
вектора, т.е.
,
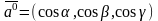если
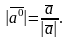
Основные действия над векторами.
Пусть
даны
и
.
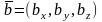Тогда:
1.
=
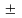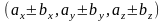
2.
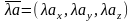, где
-действительное
число.
3.
Скалярное
произведение
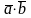двух
векторов
и
есть число, по определению равное
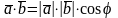,где
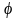-угол
между двумя векторами
и
вычисляется по формуле:
.
4.
Векторное
произведение
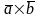двух векторов
и
- есть вектор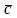
,
удовлетворяющий трем условиям:
вектор направлен так, что векторы , и образуют правую тройку;
2)
вектор
ортогонален вектора
и
,
т.е.
,
.
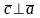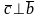3)
модуль
,
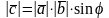де
-
угол между двумя векторами
и
.
Геометрически модуль векторного
произведения равен площади параллелограмма,
построенного на этих векторах, т.е.
.
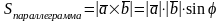Тогда
.
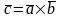5.
Смешанное
произведение
трех векторов
,
и
есть число равное по определению:
.
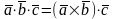Геометрически
модуль смешанного произведения равен
объему параллепипеда, построенного
на этих векторах, т.е.
.
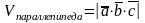Заметим, что объем тетраэдра, построенного
на трех векторах
,
и
равен
,
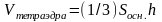где Sосн.
– площадь основания тетраэдра, h
–высота тетраэдра, т.к. основание
тетраэдра есть треугольник, построенный
на векторах
и
,
то Sосн=(1/2)
Sпараллелограмма,
следовательно,
.
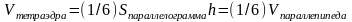Если
заданы векторы в координатах
,
и
,
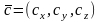то
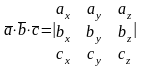смешанное
произведение.
1)
Условие перпендикулярности векторов
(
):
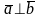или
.
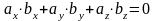2) Условие коллинеарности векторов ( // ):
или
=
=
.
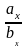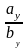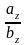3)
Условие компланарности векторов
,
,
:
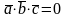или
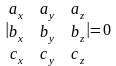
Пример. Вычислить объем тетраэдра с вершинами в точках А1, А2, А3, А4 и его высоту, опущенную из вершины А4 на грань А1 А2 А3(рис.2).
Дано: А1(-1;2;-3), А2(4;-1;0), А3(2;1;-2); А4(3;4;5).
Требуется найти объем тетраэдра.
Решение. а) Объем тетраэдра равен 1/6 части объема
параллелепипеда, построенного на векторах
,
,
.
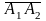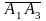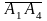Объем соответствующего параллелепипеда
вычисляется через смешанное произведение
векторов, совпадающих с ребрами тетраэдра,
сходящимися в вершине А1(рис.7.1):
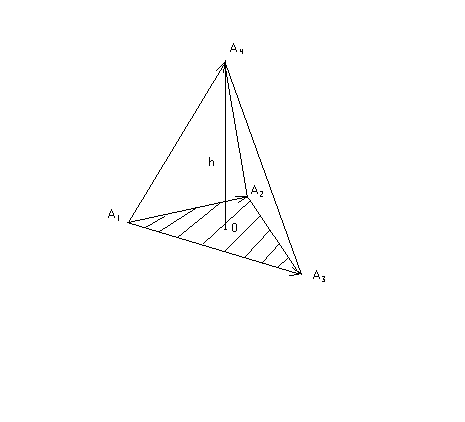
Рис. 7.1
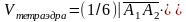
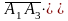
Найдем
координаты векторов и их смешанное
произведение:
,
,
=
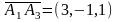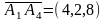
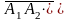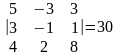
Откуда
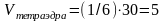(куб. ед.)
б)
Искомую высоту h
найдем из формулы:
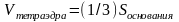h
, где Sоснования
равна площади треугольника А1
А2
А3.
Площадь треугольника А1 А2 А3 равна половине площади параллелограмма, построенного на векторах ,
Поэтому находим векторное произведение
=
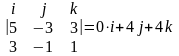
Следовательно,
Sоснования=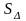
=
=
=
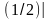
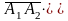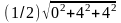=2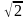
(кв.ед.)
Таким образом
h=3Vтетраэдра/Sоснования=3.5/(2 )=15 /4
Ответ:Vтетраэдра=5 (куб. ед.), h=15 /4(ед. длины)