- •Введение
- •Определители, матрицы. Системы линейных уравнений
- •2. Линейные пространства.
- •Решение систем линейных уравнений
- •3. Подпространства, образованные решениями линейной однородной системы (лос) уравнений. Нахождение общего решения лос
- •4. Линейные преобразования и действия Над ними
- •5. Собственные значения и собственые векторы матрицы
- •6. Приведение квадратичной формы к каноническому виду
- •7. Векторы и действия над ними
- •8. Плоскость и прямая в пространстве
- •9. Кривые второго порядка на плоскости
- •10. Приведение общего уравнения кривой второго порядка к каноническому виду
- •11. Исследование общего уравнения кривой. Поверхности второго порядка.
- •12. Комплексные числа. Теорема
- •И ее предел.
- •13. Функция. Предел функции
- •14. Применение эквивалентных бесконечно малых к вычислению пределов
- •15. Производная функции и ее вычисление
- •16. Дифференциал функции. Применение дифференциала
- •17. Неопределенный интеграл
- •18. Определенный интеграл
- •19. Несобственные интегралы
- •20. Приложения определённого интеграла
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •21. Функции нескольких переменных Основные теоретические сведения
- •22. Частные производные первого порядка. Полный дифференциал функции и его применение к приближенным вычислениям
- •1) Случай одной независимой переменной.
- •23. Производные и дифференциалы высших порядков
- •1) Случай одной независимой переменной.
- •2) Случай нескольких независимых переменных.
- •24. Формула Тейлора для функции двух переменных
- •25. Экстремум функции нескольких независимых переменных
- •26. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •27. Дифференциальные уравнения
- •28. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •29. ЧиСлоВые ряды
- •30. Функциональные ряды
- •31. Тригонометрические ряды Фурье
- •32. Интеграл Фурье
- •33. Двойной интеграл
- •34. Тройные интегралы
- •35. Криволинейные интегралы
- •36. Поверхностные интегралы
- •Поверхностные интегралы второго рода
- •Так же получены формулы:
- •37. Теория поля
- •Скалярные поля
- •Формула Остроградского на плоскости
- •Циркуляция вектора вдоль контура не зависит от выбора координатной системы.
- •38. Оператор Гамильтона
- •Дифференциальные операции второго порядка
- •39. Функция комплексного переменного
- •40. Дифференцирование функций комплексного переменного, условия коши — римана
- •41. Интегрирование функций комплексного переменного
- •42. Ряд лорана
- •43. Преобразование Лапласа
- •44. Задача коши для обыкновенных линейных дифференциальных уравнений
- •Заключение
- •Библиографический список
- •35. Криволинейные интегралы ……………………………….302
- •394026 Воронеж, Московский просп.,14
44. Задача коши для обыкновенных линейных дифференциальных уравнений
Решение линейных дифференциальных уравнений операционным методом предполагает три этапа: 1) переход от исходных функций к их изображениям по Лапласу, при этом дифференциальное уравнение преобразуется в алгебраическое относительно изображения искомой функции; 2) решение полученного алгебраического уравнения; 3) получение искомого решения по его изображению.
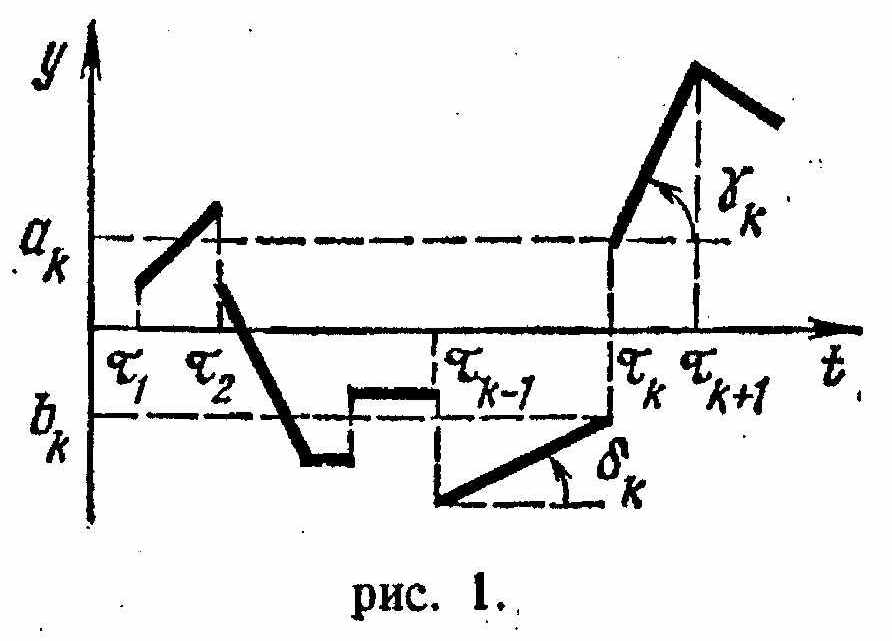
Рис. 44.1
Решим
Задачу Коши для дифференциального
уравнения
![]() при начальном условии x(0)=1.
Операционный метод решения такой задачи
состоит в том, что искомую функцию и
правую часть дифференциального уравнения
считаем оригиналами и переходим от
уравнения, связывающего оригиналы, к
уравнению, связывающему их изображения.
Воспользуемся формулой дифференцирования
оригинала
при начальном условии x(0)=1.
Операционный метод решения такой задачи
состоит в том, что искомую функцию и
правую часть дифференциального уравнения
считаем оригиналами и переходим от
уравнения, связывающего оригиналы, к
уравнению, связывающему их изображения.
Воспользуемся формулой дифференцирования
оригинала
![]() Применяя
свойство линейности, перейдём в уравнении
от оригинала к изображениям:
Применяя
свойство линейности, перейдём в уравнении
от оригинала к изображениям:
![]() Решим
полученное уже не дифференциальное, а
алгебраическое уравнение относительно
неизвестного изображения X(p):
Решим
полученное уже не дифференциальное, а
алгебраическое уравнение относительно
неизвестного изображения X(p):
![]() Осталось по неизвестному изображению
X(p)
найти соответствующий ему оригинал
x(t).
Используя свойство линейности
преобразования Лапласа и табличные
операционные соотношения, получаем
Осталось по неизвестному изображению
X(p)
найти соответствующий ему оригинал
x(t).
Используя свойство линейности
преобразования Лапласа и табличные
операционные соотношения, получаем
![]() Это
и есть искомое решение задачи Коши.
Аналогично решаются системы линейных
дифференциальных уравнений.
Это
и есть искомое решение задачи Коши.
Аналогично решаются системы линейных
дифференциальных уравнений.
Формула Дюамеля
Рассмотрим линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами:
![]()
при нулевых начальных условиях
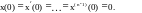
(Заменой
искомой функции задачу с ненулевыми
начальными условиями можно свести к
задаче с нулевыми условиями.). Допустим,
что известно решение уравнения
![]() (с
той же левой частью и правой частью,
равной единице) при нулевых условиях.
Обозначим его
(с
той же левой частью и правой частью,
равной единице) при нулевых условиях.
Обозначим его
![]() Тогда решение x(t)
задачи
Коши можно выразить через
Тогда решение x(t)
задачи
Коши можно выразить через
![]() с помощью одной из формул:
с помощью одной из формул:
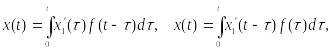
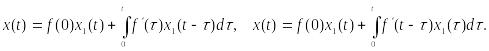
Каждое из этих выражений называют формулой (или интегралом) Дюамеля. Метод решения дифференциальных уравнений, основанный на формуле Дюамеля, применяют, как правило, в тех случаях, когда возникают трудности при нахождении изображения F(p) правой части f(t) , а также при необходимости многократного решения задачи для различных функций f(t)
Пример 1 . На материальную точку массы m действует сила сопротивления R = kv, пропорциональная скорости. Какое расстояние пройдёт точка за неограниченное время, если ей сообщена начальная скорость v0 ? k = m, v0 = 7 м/с.
Решение:
Исходя из второго закона Ньютона: am=
- kv,![]() .
Начальные условия:
.
Начальные условия:![]() ,
x
(0) = 0. Подставим значения k:
,
x
(0) = 0. Подставим значения k:![]() .
Сократим все выражения на m:
.
Сократим все выражения на m:
![]() .
Перейдём к изображениям функций:
.
Перейдём к изображениям функций:
p 2 X (p) – px (0) – x (0) –pX(p) – x (0) = 0,
p (p+1)X (p) – 7 = 0, p (p+1)X (p) = 7
X
(p) =
![]()
По такому изображению легко найти оригинал:
x (t)=7 – 7 e -t .
Пример 2 . Найти решение задачи Коши
![]()
Решение: Вначале решим вспомогательную задачу
![]()
Если
![]() соответствует изображение
соответствует изображение
![]() то переходят от оригиналов функций к
их изображениям, получим
то переходят от оригиналов функций к
их изображениям, получим
![]()
Разложим дробь на простые дроби, получим
![]()
По таблице оригиналов .
Найдем
![]()
Используя
формулу Дюамеля, получим искомое решение