
- •Введение
- •Определители, матрицы. Системы линейных уравнений
- •2. Линейные пространства.
- •Решение систем линейных уравнений
- •3. Подпространства, образованные решениями линейной однородной системы (лос) уравнений. Нахождение общего решения лос
- •4. Линейные преобразования и действия Над ними
- •5. Собственные значения и собственые векторы матрицы
- •6. Приведение квадратичной формы к каноническому виду
- •7. Векторы и действия над ними
- •8. Плоскость и прямая в пространстве
- •9. Кривые второго порядка на плоскости
- •10. Приведение общего уравнения кривой второго порядка к каноническому виду
- •11. Исследование общего уравнения кривой. Поверхности второго порядка.
- •12. Комплексные числа. Теорема
- •И ее предел.
- •13. Функция. Предел функции
- •14. Применение эквивалентных бесконечно малых к вычислению пределов
- •15. Производная функции и ее вычисление
- •16. Дифференциал функции. Применение дифференциала
- •17. Неопределенный интеграл
- •18. Определенный интеграл
- •19. Несобственные интегралы
- •20. Приложения определённого интеграла
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •21. Функции нескольких переменных Основные теоретические сведения
- •22. Частные производные первого порядка. Полный дифференциал функции и его применение к приближенным вычислениям
- •1) Случай одной независимой переменной.
- •23. Производные и дифференциалы высших порядков
- •1) Случай одной независимой переменной.
- •2) Случай нескольких независимых переменных.
- •24. Формула Тейлора для функции двух переменных
- •25. Экстремум функции нескольких независимых переменных
- •26. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •27. Дифференциальные уравнения
- •28. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •29. ЧиСлоВые ряды
- •30. Функциональные ряды
- •31. Тригонометрические ряды Фурье
- •32. Интеграл Фурье
- •33. Двойной интеграл
- •34. Тройные интегралы
- •35. Криволинейные интегралы
- •36. Поверхностные интегралы
- •Поверхностные интегралы второго рода
- •Так же получены формулы:
- •37. Теория поля
- •Скалярные поля
- •Формула Остроградского на плоскости
- •Циркуляция вектора вдоль контура не зависит от выбора координатной системы.
- •38. Оператор Гамильтона
- •Дифференциальные операции второго порядка
- •39. Функция комплексного переменного
- •40. Дифференцирование функций комплексного переменного, условия коши — римана
- •41. Интегрирование функций комплексного переменного
- •42. Ряд лорана
- •43. Преобразование Лапласа
- •44. Задача коши для обыкновенных линейных дифференциальных уравнений
- •Заключение
- •Библиографический список
- •35. Криволинейные интегралы ……………………………….302
- •394026 Воронеж, Московский просп.,14
23. Производные и дифференциалы высших порядков
Частные производные высших порядков.
Частными производными второго порядка функции называются частные производные от её частных производных первого порядка.
Обозначения частных производных второго порядка:
![]() ;
;![]() ,
,
![]() ;
;![]() .
.
Аналогично
определяются и обозначаются частные
производные третьего и выше третьего
порядков; например:
![]() ;
;![]() и т.п.
и т.п.
Символ
![]() обозначает частную производную третьего
порядка функции
,
вычисленную три раза по х; символ
обозначает частную производную третьего
порядка функции
,
вычисленную три раза по х; символ
![]() обозначает, что от функции z
взята частная производная третьего
порядка, причём она вычисляется два
раза по х и от полученной производной
обозначает, что от функции z
взята частная производная третьего
порядка, причём она вычисляется два
раза по х и от полученной производной
![]() вычислена один раз производная по у.
Имеет место такая важная теорема: если
частные производные непрерывны, то их
значения не зависят от порядка
дифференцирования.
Таким образом, так называемые смешанные
производные,
отличающиеся друг от друга лишь
последовательностью дифференцирования
, равны между собой, если они непрерывные
функции, например:
вычислена один раз производная по у.
Имеет место такая важная теорема: если
частные производные непрерывны, то их
значения не зависят от порядка
дифференцирования.
Таким образом, так называемые смешанные
производные,
отличающиеся друг от друга лишь
последовательностью дифференцирования
, равны между собой, если они непрерывные
функции, например:![]() .
.
Пример
1 . Найти
частные производные второго порядка
от следующих функций: а) z=2xy;
б) z=ln(x2+y2);
в)
![]() /
/
Решение. Находим сначала частные производные первого порядка. Затем их дифференцируем вторично:
а)![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
б)
Находим![]() ;
;
![]() ;
далее
;
далее
находим
![]() ;
;
![]() ;
;
![]() .
.
в) Имеем
 ;
;
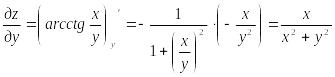 ;
;
Теперь
находим:
![]() ;
;
![]() ;
;
![]() .
.
Дифференциалы высших порядков.
Дифференциалом
второго порядка
от функции
называется дифференциал от её полного
дифференциала (первого порядка), т.е.
![]() .
.
Аналогично
определяются дифференциалы функции z
порядка
выше второго , например:
![]() ,
т.е. дифференциалом третьего порядка
от функции z
есть
дифференциал от её дифференциала второго
порядка. Вообще,
,
т.е. дифференциалом третьего порядка
от функции z
есть
дифференциал от её дифференциала второго
порядка. Вообще,
![]() ,
,
![]() .
Если
,
где аргументы х
и у –независимые
переменные и функция
.
Если
,
где аргументы х
и у –независимые
переменные и функция
![]() имеет непрерывные частные производные,
то дифференциалы высших порядков
вычисляются по формулам:
имеет непрерывные частные производные,
то дифференциалы высших порядков
вычисляются по формулам:
![]()
![]() .
.
Вообще,
при наличии соответствующих производных
справедлива символическая формула для
дифференциала порядка n
:
![]() ,
которая формально раскрывается по
биноминальному закону. Если
,
где аргументы
,
которая формально раскрывается по
биноминальному закону. Если
,
где аргументы
![]() и
и
![]() являются функциями одного или нескольких
независимых переменных, то
являются функциями одного или нескольких
независимых переменных, то
![]()
Если
х
и у
– независимые переменные, то
![]() и
и
![]() - величины постоянные, поэтому
- величины постоянные, поэтому
![]() ,
,
![]() .
Заметим, что следующая запись означает
.
Заметим, что следующая запись означает
![]() ,
выражение
,
выражение
![]() следует понимать, как выражение
следует понимать, как выражение![]() и т.д. Кроме способа вычисления
дифференциалов функции по формулам,
есть другой способ нахождения
дифференциалов высших порядков, который
даёт возможность определить их, минуя
вычисление частных производных; далее
по известному выражению дифференциала
мы сможем находить и частные производные.
Этот способ состоит в последовательном
дифференцировании. Рассмотрим следующий
пример.
и т.д. Кроме способа вычисления
дифференциалов функции по формулам,
есть другой способ нахождения
дифференциалов высших порядков, который
даёт возможность определить их, минуя
вычисление частных производных; далее
по известному выражению дифференциала
мы сможем находить и частные производные.
Этот способ состоит в последовательном
дифференцировании. Рассмотрим следующий
пример.
Пример
2. Найти
дифференциалы первого и второго порядков
функции
![]() .
.
Решение.
Имеем
![]() ;
;
![]() поэтому
поэтому
![]() .
Далее находим
.
Далее находим
![]() ;
;![]() ;
;
![]() .
Имеем:
.
Имеем:
![]() .
.
Дифференцирование неявных функций.
1) Случай одной независимой переменной.
Пусть
![]() -неявная
функция , т.е. она определяется из
уравнения
-неявная
функция , т.е. она определяется из
уравнения
![]() ,
не разрешённого относительно
.
Это значит, что при каждом значении
,
не разрешённого относительно
.
Это значит, что при каждом значении
![]() ,
при котором неявная функция определена,
она принимает единственное значение
,
при котором неявная функция определена,
она принимает единственное значение
![]() так, что
так, что
![]() .
Если
.
Если
![]() -
дифференцируемая функция переменных
и
,
то производная неявной функции
-
дифференцируемая функция переменных
и
,
то производная неявной функции
![]() ,
заданной с помощью уравнения
,
может быть найдена по формуле
,
заданной с помощью уравнения
,
может быть найдена по формуле
![]() ,
при условии, что
,
при условии, что
![]() Формула позволяет находить n-ую
производную
от
по
,
зная
Формула позволяет находить n-ую
производную
от
по
,
зная
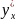 (вычисляя от
следующие производные).
(вычисляя от
следующие производные).
Пример
3 .
Найти
![]() ,
если функция
задана неявно уравнением
,
если функция
задана неявно уравнением
![]() ,
где
,
где
![]() -величина
постоянная.
-величина
постоянная.
Решение.
Обозначим левую часть данного уравнения
![]() .
Найдём её частные производные
.
Найдём её частные производные
![]() ,
,
![]() .
.
Применив
формулу
, получаем
![]() .
.
