
- •Введение
- •Определители, матрицы. Системы линейных уравнений
- •2. Линейные пространства.
- •Решение систем линейных уравнений
- •3. Подпространства, образованные решениями линейной однородной системы (лос) уравнений. Нахождение общего решения лос
- •4. Линейные преобразования и действия Над ними
- •5. Собственные значения и собственые векторы матрицы
- •6. Приведение квадратичной формы к каноническому виду
- •7. Векторы и действия над ними
- •8. Плоскость и прямая в пространстве
- •9. Кривые второго порядка на плоскости
- •10. Приведение общего уравнения кривой второго порядка к каноническому виду
- •11. Исследование общего уравнения кривой. Поверхности второго порядка.
- •12. Комплексные числа. Теорема
- •И ее предел.
- •13. Функция. Предел функции
- •14. Применение эквивалентных бесконечно малых к вычислению пределов
- •15. Производная функции и ее вычисление
- •16. Дифференциал функции. Применение дифференциала
- •17. Неопределенный интеграл
- •18. Определенный интеграл
- •19. Несобственные интегралы
- •20. Приложения определённого интеграла
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •21. Функции нескольких переменных Основные теоретические сведения
- •22. Частные производные первого порядка. Полный дифференциал функции и его применение к приближенным вычислениям
- •1) Случай одной независимой переменной.
- •23. Производные и дифференциалы высших порядков
- •1) Случай одной независимой переменной.
- •2) Случай нескольких независимых переменных.
- •24. Формула Тейлора для функции двух переменных
- •25. Экстремум функции нескольких независимых переменных
- •26. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •27. Дифференциальные уравнения
- •28. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •29. ЧиСлоВые ряды
- •30. Функциональные ряды
- •31. Тригонометрические ряды Фурье
- •32. Интеграл Фурье
- •33. Двойной интеграл
- •34. Тройные интегралы
- •35. Криволинейные интегралы
- •36. Поверхностные интегралы
- •Поверхностные интегралы второго рода
- •Так же получены формулы:
- •37. Теория поля
- •Скалярные поля
- •Формула Остроградского на плоскости
- •Циркуляция вектора вдоль контура не зависит от выбора координатной системы.
- •38. Оператор Гамильтона
- •Дифференциальные операции второго порядка
- •39. Функция комплексного переменного
- •40. Дифференцирование функций комплексного переменного, условия коши — римана
- •41. Интегрирование функций комплексного переменного
- •42. Ряд лорана
- •43. Преобразование Лапласа
- •44. Задача коши для обыкновенных линейных дифференциальных уравнений
- •Заключение
- •Библиографический список
- •35. Криволинейные интегралы ……………………………….302
- •394026 Воронеж, Московский просп.,14
22. Частные производные первого порядка. Полный дифференциал функции и его применение к приближенным вычислениям
Частные производные первого порядка
Если
![]() и одна из переменных, например x,
получила приращение
и одна из переменных, например x,
получила приращение
![]() (при постоянных других переменных y
и z),
то разность
(при постоянных других переменных y
и z),
то разность
![]() называется частным приращением по
называется частным приращением по
![]() функции
функции
![]()
![]() .
Соответственно, имеем частные приращения
функции по y
и по z
.
Соответственно, имеем частные приращения
функции по y
и по z
![]() ,
,
![]()
Частной
производной
от функции
![]()
![]() по
независимой переменной
называется производная
по
независимой переменной
называется производная
![]()
![]() ,
или в более подробной записи
,
или в более подробной записи
![]()
![]() ,
,
вычисленная
при постоянных y,z.
Обозначается одним из символов
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Аналогично, предел отношения
.
Аналогично, предел отношения
![]() при стремлении
при стремлении
![]() к нулю называется частной производной
функции по y:
к нулю называется частной производной
функции по y:
![]() .
.
![]() Частная
производная по z
есть производная
Частная
производная по z
есть производная
![]() ,
равная пределу
,
равная пределу
![]() ,
то есть
,
то есть
![]()
![]() .
.
Очевидно, что для нахождения частных производных справедливы обычные правила и формулы дифференцирования; только следует иметь в виду, что при нахождении частной производной надо считать постоянными все независимые переменные, кроме той, по которой берется частная производная.
Пример 1 . Найти частные производные функции
![]() .
.
Решение.
Рассматривая переменные
![]() ,
,
![]() как постоянные величины, получим
как постоянные величины, получим
![]() .
Считая
,
постоянными, дифференцируем функцию
по
:
.
Считая
,
постоянными, дифференцируем функцию
по
:
![]() .
Аналогично, дифференцируем функцию по
z,
считая x,y
постоянными:
.
Аналогично, дифференцируем функцию по
z,
считая x,y
постоянными:
![]() .
.
Полный дифференциал функции.
Полным
приращением
функции
![]() двух независимых переменных в точке
M(x,y)
называется разность
двух независимых переменных в точке
M(x,y)
называется разность
![]() ,
,
где и – произвольные приращения аргументов.
Функция
называется дифференцируемой
в точке (x,y),
если в этой точке полное приращение
![]() можно представить в виде
можно представить в виде
![]() ,
где слагаемое
,
где слагаемое
![]() есть бесконечно малая величина высшего
порядка по сравнению с бесконечно малой
есть бесконечно малая величина высшего
порядка по сравнению с бесконечно малой
![]() .
.
Полным дифференциалом функции называется главная часть ее полного приращения , линейная относительно приращений аргументов и , то есть
![]() .
.
Дифференциалы
dx,
dy
независимых переменных x
и y
совпадают с их приращениями,
то есть
![]() ,
,
![]() – это числа, равные между собой. Полный
дифференциал функции
вычисляется по формуле:
– это числа, равные между собой. Полный
дифференциал функции
вычисляется по формуле:
![]() ,
где
,
где
![]() ,
,
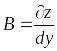
Аналогично,
полный дифференциал функции трех
аргументов
![]() вычисляется по формуле
вычисляется по формуле
![]()
Заметим,
что в выражениях
![]() ,
,
![]()
![]() скобки можно опустить, так как
,
рассматриваются как единый символ.
Функция заведомо имеет полный дифференциал
в случае непрерывности
ее частных производных.
Значит, если функция имеет полный
дифференциал, то она дифференцируема.
скобки можно опустить, так как
,
рассматриваются как единый символ.
Функция заведомо имеет полный дифференциал
в случае непрерывности
ее частных производных.
Значит, если функция имеет полный
дифференциал, то она дифференцируема.
Применения полного дифференциала
к приближенным вычислениям.
Имеем
связь между полным дифференциалом
функции и ее полным приращением:
![]() .
.
Вычисление
(приращения функции) представляет собой
задачу, более трудоемкую, чем вычисление
ее дифференциала dz,
а потому в практических вычислениях с
достаточной точностью при малых
приращениях аргументов заменяют
вычисление приращения функции вычислением
ее дифференциала. При достаточно малых
![]() ,
,![]() ,
а значит, при достаточно малом
,
а значит, при достаточно малом
![]() для дифференцируемой функции
для дифференцируемой функции
![]()
![]() имеет место приближенное равенство
имеет место приближенное равенство
![]() или
или
![]() .
Итак, получим
.
Итак, получим
![]() или
или
![]() ,
где
,
где
![]() ,
,
![]() .
Это приближенное равенство тем точно,
чем меньше величины
,
.
.
Это приближенное равенство тем точно,
чем меньше величины
,
.
Пример
2 . Вычислить
приближенно величину![]()
Решение:
Рассмотрим
функцию
![]() .
Воспользуемся формулой. Имеем
.
Воспользуемся формулой. Имеем
![]() ,
,
![]() ,
,
![]() ,
,
![]() Значение функции
в точке
Значение функции
в точке
![]() :
:
![]() .
Вычисляем
.
Вычисляем
![]() ,
где
;
;
откуда
,
где
;
;
откуда
![]() .
Значит,
.
Значит,
![]() .
.
Дифференцирование сложной функции
