14. Применение эквивалентных бесконечно малых к вычислению пределов
Пусть
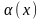и
-
бесконечно малые функции, при
,
т.е.
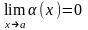и
,
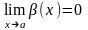причем a может быть
как числом, так и одним из символов
,
-
.
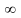Бесконечно
малые функции
и
называются бесконечно малыми одного
порядка, если предел их отношения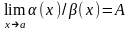
,
.
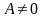Если же число А=0, то бесконечно
малая
называется бесконечно малой более
высокого порядка малости по сравнению
с
.
Если
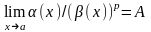и
, то бесконечно малая функция
называется бесконечно малой порядка
p по сравнению с
бесконечно малой функцией
.
Бесконечно малые функции
и
называются эквивалентными, если
.
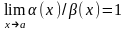В этом случае пишут:
~
.
Теорема (о замене бесконечно малых функций им эквивалентными ). Предел отношения двух бесконечно малых функций не изменяется, если каждую из них или какую-либо одну заменить им эквивалентными функциями.
Если при некотором предельном переходе функция есть бесконечно малая, то Sin( )~ , tg( )~ ;
arcsin(
)~
,
arctg(
)~
;
ln(1+
)~
,
ln(1+k
)~k
,
~
,
~
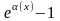ln
a
Первый замечательный предел
Во многих случаях используется
первый замечательный предел
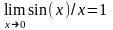(х- длина дуг или угол, выраженный в
радианах) и предполагается известным,
что
.
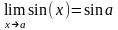Иногда при отыскании предела полезно
сделать замену переменной с
тем, чтобы упростить вычисление предела
и использовать известные пределы. Если
пол знаком предела делается замена
переменной, то все величины, находящиеся
под знаком, должны быть выражены через
эту новую переменную. Из равенства,
выражающего зависимость между старой
переменной и новой, надо определить
предельное значение новой переменной.
Например, при нахождении предела
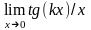обозначаем t=kx
, где при
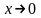новая переменная
,
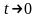x=t/k.
Тогда
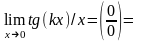
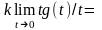
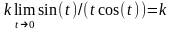
(т.к.cos
(0)=1). Полезно
помнить, что
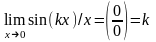, где k
-постоянная величина. Например, при
функция sin(x)
и tg(x)
эквивалентные
бесконечно
малые, т.е. sin(x)~tg(x);
т.к.
.
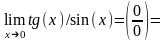
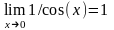Пример
1.
Найти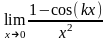
Решение. Применим сначала формулу тригонометрии
1-cos(t)=2sin2(t/2).
У нас
1-cos(kx)=2sin2(kx/2),
при
;
sin2(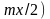
)~(
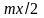)2.
По теореме “замены эквивалентной”
получим
.
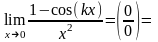
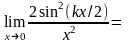
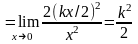Заметим, что можно было воспользоваться
первым замечательным пределом.
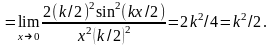Ответ: k2/2.
Пример
2.
Вычислить
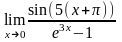
Решение. По формуле тригонометрии sin(5(x+π))=sin(5x+5π)=- sin(5x).
Тогда
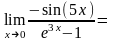
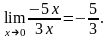
Поскольку при , sin(5x)~5x, e3x-1~ 3x
Ответ:-5/3.
Вычисление предела показательно-степенной функции
При
нахождении пределов вида
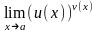=C
Следует иметь ввиду, что:
1) если существуют конечные пределы
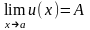и
,
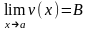то C=AB,
т.е.
имеет
место формула
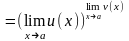
Заметим,
что предельное значение а может
обозначать и число, и один из символов
;
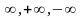2)
есл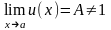и
и
,
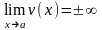то вопрос о нахождении
затруднений обычно не вызывает. В том
случае полезны иногда формулы:
;
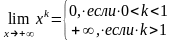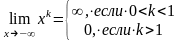
3)
есл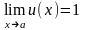и
и
,
т.е. имеем неопределенность вида {
},
то полагают
,
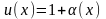где
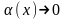при
и,
следовательно,
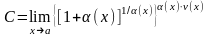
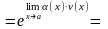
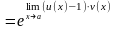
Проиллюстрируем общий прием вычисления пределов на следующем примере ( раскрытие неопределенности вида { }).
Пример
3. Найти
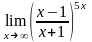
Решение.
Здесь
основание степени
при
,
а показатель степени
,
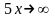т.е. имеется неопределенность вида
.
Тогда
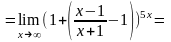
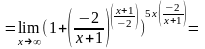
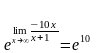
(Получили
в качестве
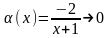при
)
Замечание
1. При
вычислении пределов выражений вида
,
где
,
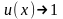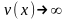при
, удобно иногда пользоваться формулой
.
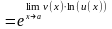Замечание 2. При вычислении пределов полезно знать, что
а)
если существует и положителен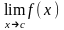
,
то
;
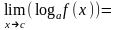
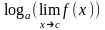б)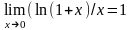
;
в)
.
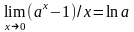