5.7. Плотность теплоёмкости равновесного фотонного газа

Как отмечалось выше в открытых термодинамических системах невозможно осуществить изопроцессы (изохорический, изотермический, изобарический, адиабатический). Следовательно, такие термодинамические характеристики как (теплоёмкость при постоянном объёме) и (теплоёмкость при постоянном давлении) ввести для равновесного фотонного газа нельзя. Однако для открытых систем можно ввести понятие плотности теплоёмкости (уравнение (1.17)). Используя это уравнение для равновесного фотонного газа как открытой системы, получим

(5.22)

5.8. Критические замечания

Авторы [8], используя выражение для внутренней энергии равновесного фотонного газа

(5.23) вводят в нём теплоёмкость при постоянном объёме

(5.24) Нетрудно видеть, что авторы рассматривают фотонный газ как закрытую систему, так как изохорический процесс уже по своему определению предполагает, что число частиц в системе должно быть постоянным. Далее авторы [8] пытаются ввести в равновесном фотонном газе адиабатический процесс. Они получают число фотонов при заданной температуре

(5.25) Затем полагают в (5.25) 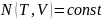и получают уравнение адиабаты

(5.26) Авторы совершенно не замечают, что условие уже предполагает, что равновесный фотонный газ является закрытой системой (системой с постоянным числом частиц). Таким образом, изучение равновесного фотонного газа как открытой системы авторы подменяют изучением его как закрытой системы. Ошибки, допущенные в работе [8], были также замечены и у авторов работ [6], [22], на что было указано в работах [1], [2].

5.9. Спектральные характеристики и интегральные законы равновесного излучения

Соотношение (4.76) с учётом того, что можно для электромагнитных волн переписать в виде [28]

(5.27) Запишем теперь уравнения (5.2), (5.3), (5.6), взяв в качестве переменной интегрирования не квантовое число , а круговую частоту согласно (5.27)

(T) = exp[ħω ] (5.28)

[ħω (5.29)

[ħω (5.30)

Далее, дифференцируя выражение по , получим выражение плотности энтропии равновесного фотонного газа

[ħω ( ] (5.31)

Дифференцируя (5.30) по , получим выражение плотности теплоёмкости равновесного фотонного газа

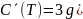
[ħω ( [ħω ( (5.32) Очевидно, при интегрировании выражений (5.28) – (5.32) по получим те же значения для , , , , , 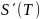которые получили при интегрировании по квантовому числу . Однако введение в формулах (5.28) – (5.32) в качестве переменной интегрирования круговой частоты приводит уже к появлению новых спектральных характеристик равновесного излучения. Так в выражении (5.28) можно ввести такую спектральную характеристику равновесного излучения, как спектральную плотность объёмной плотности числа фотонов

[ħω ( (5.33) Тогда имеем

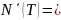
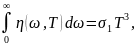(5.34) где

(5.35) Уравнение (5.34) выражает один из интегральных законов равновесного с веществом излучения. Согласно этому закону плотность числа фотонов при равновесном излучении пропорционально абсолютной температуре в третьей степени.

Далее можно ввести ещё одну спектральную характеристику равновесного излучения – спектральную плотность объёмной плотности внутренней энергии равновесного фотонного газа

[ħω (5.36)

Тогда

(5.37)

где

(5.38) постоянная Стефана-Больцмана. Выражение в (5.37) представляет собой закон Стефана-Больцмана, который утверждает, что объёмная плотность внутренней энергии равновесного фотонного газа пропорциональна абсолютной температуре в четвёртой степени.

Введём ещё одну спектральную характеристику равновесного излучения – спектральную плотность объёмной плотности свободной энергии фотонного равновесного газа

[ħω (5.39)

Тогда

(5.40) где

(5.41) Уравнение (5.41) выражает ещё один интегральный закон равновесного излучения, согласно

которому объёмная плотность свободной энергии равновесного фотонного газа пропорциональна абсолютной температуре в четвёртой степени.

Вводя ещё одну спектральную характеристику равновесного излучения – спектральную плотность объёмной плотности энтропии равновесного фотонного газа, получим

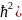
[ħω ( (5.42) Согласно (5.21) и (5.42)

(5.43) где

(5.44) Уравнение (5.44) выражает также интегральный закон равновесного излучения, согласно которому плотность энтропии равновесного фотонного газа пропорциональна абсолютной температуре в третьей степени.

Наконец, можно ввести последнюю характеристику равновесного излучения – спектральную плотность объёмной плотности теплоёмкости равновесного фотонного газа

[ħω ( (5.45) С учётом (5.22) и (5.32)

(5.46)

где

(5.47)

Уравнение (5.46) выражает последний пятый интегральный закон равновесного излучения, согласно которому объёмная плотность теплоёмкости равновесного фотонного газа пропорциональна абсолютной температуре в третьей степени.