1.3. Основные этапы проектирования ких-фильтров
На рис. 1.5 показана схема, поясняющая основные этапы проектирования нерекурсивных цифровых фильтров.
Первый этап – формулировка задачи аппроксимации – включает в себя следующие шаги:
выбор типа фильтра (с линейной ФЧХ определённого вида или другого);
выбор аппроксимирующей функции
,
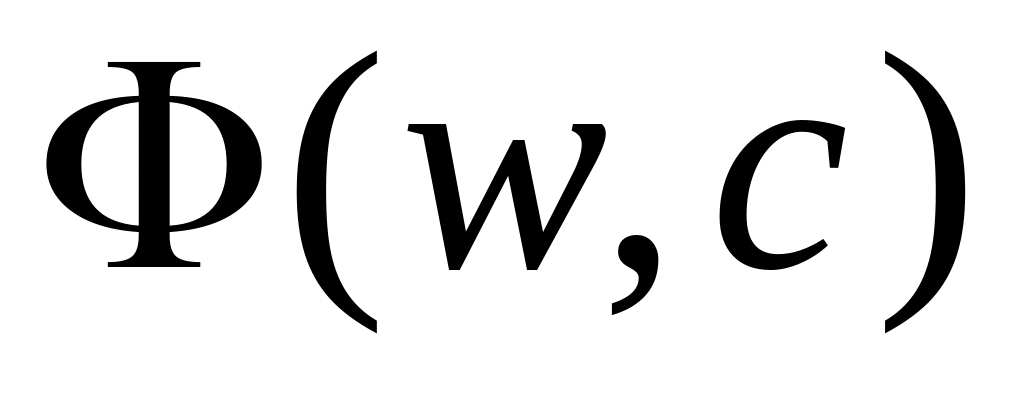значения которого определяют требуемую
характеристику фильтра, например АЧХ.
Здесь
-
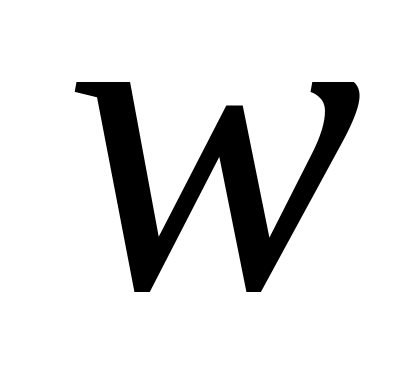нормированная частота;
-
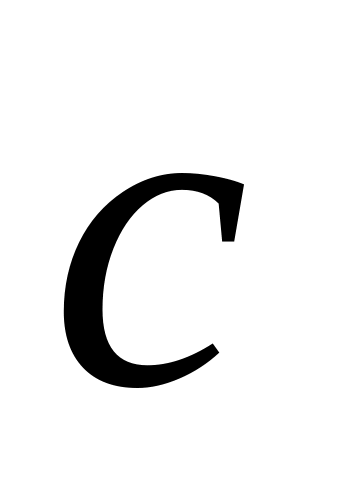вектор коэффициентов, совпадающий с
вектором коэффициентов фильтра b
или достаточно просто связанный с ним;определение аппроксимируемой функции
,
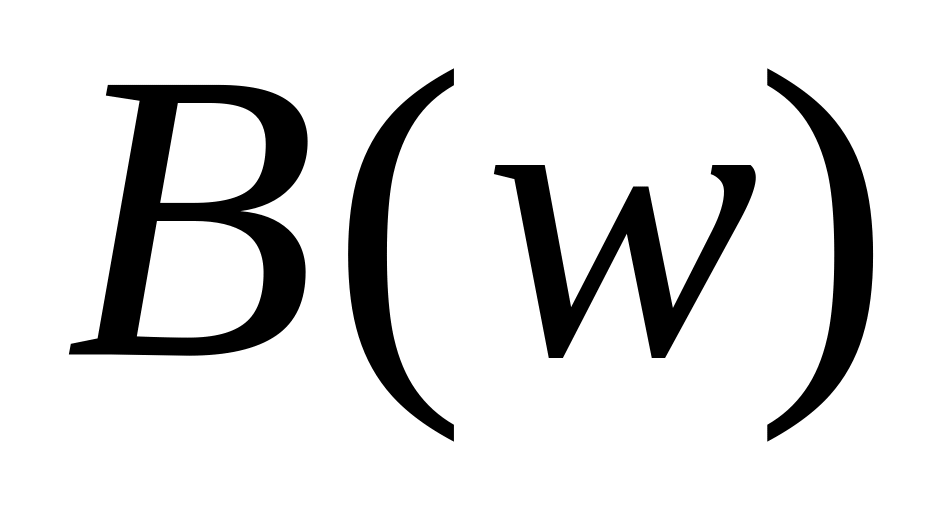задающей требования к заданной
характеристике;
Рис.1.5. Основные этапы проектирования нерекурсивных цифровых фильтров.
выбор критерия аппроксимации, то есть уточнение смысла приближённого равенства,
(1.14)
при заданных значениях ;
определение весовой функции аппроксимации
,
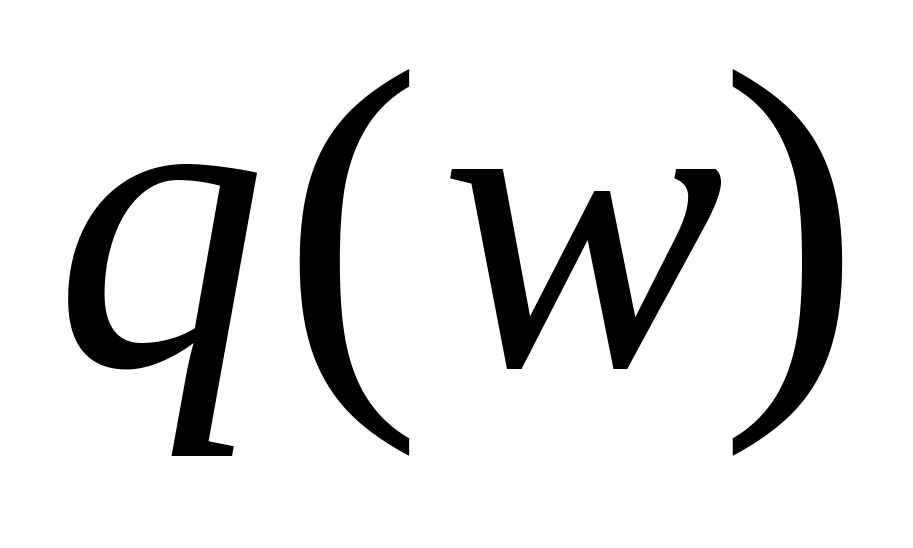задающей требования к точности
приближённого равенства (1.14).
Целью первого этапа является математическая
формулировка задачи вычисления вектора
по заданным требованиям к характеристикам
фильтра.
Второй этап – решение задачи аппроксимации - включает в себя следующие шаги:
оценку необходимого порядка фильтра N;
расчёт вектора коэффициентов ;
проверку критерия получения решения (выполнение заданных требований к характеристикам фильтра).
Если требования к характеристикам
выполняются, то по вектору коэффициентов
определяется вектор b и
второй этап заканчивается. Если требования
не выполняются, необходимо вернуться
ко второму шагу и рассчитать вектор
при большем значении N.
Целью второго этапа является определение вектора коэффициентов фильтра b.
Третий этап – расчёт разрядности
коэффициентов (или разрядности регистров
ПЗУ) – зависит от выбранной элементной
базы. При реализации фильтра на ПЛИС
необходимо минимизировать значение
,
уменьшая его до тех пор, пока заданные
требования перестанут выполняться.
На четвёртом этапе рассчитываются разрядности регистров оперативной памяти таким образом, чтобы мощность собственных шумов фильтра была меньше, чем мощность шума на входе. На пятом этапе осуществляется схемная реализация фильтра на выбранной элементной базе.
Рассмотрим теперь различные постановки задач аппроксимации.
Целью решения аппроксимационной задачи
является определение коэффициентов
передаточной функции фильтра.
Аппроксимирующая функция
должна удовлетворять следующим
требованиям:
вектор должен быть связан простой зависимостью с вектором коэффициентов b;
функция должна достаточно просто зависеть от вектора ;
при заданных значениях должно выполняться (1.14).
Наиболее простой и удобной для решения
задачи аппроксимации является линейная
зависимость функции
от вектора
:
.
(1.15)
Существуют два основных критерия аппроксимации, уточняющие смысл (1.14):
среднеквадратический критерий
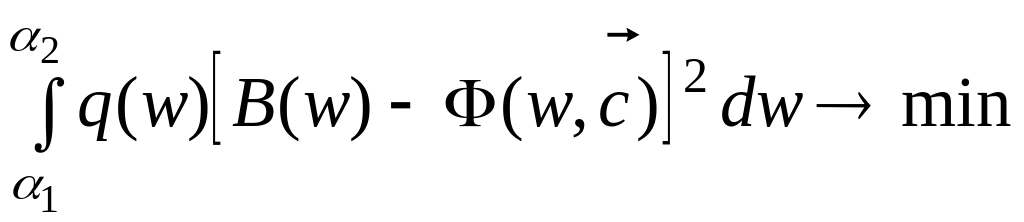(1.16)
и наилучший равномерный (чебышевский) критерий
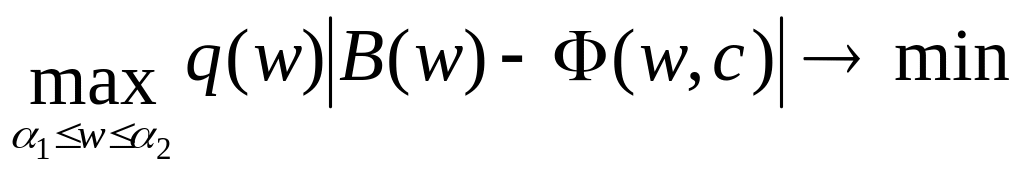(1.17)
Критерии (1.16) и (1.17) могут применяться совместно – каждый для определённой области частот. Выбор критерия аппроксимации определяется физическим смыслом задачи.
Общий принцип определения значений
весовой функции
состоит в следующем: чем точнее должно
выполняться (1.14) при
,
тем больше должно быть значение
.
При использовании критерия (1.17) для
отдельных подынтервалов частот
задаются значения
такие, чтобы на этих подынтервалах
выполнялось неравенство:
.
(1.18)
Тогда для j-го подынтервала:
,
(1.19)
где R – произвольная константа (нормирующий множитель), общая для всех подынтервалов.
Для избирательных фильтров с линейной
ФЧХ аппроксимируемые функции имеют
вид: в полосах пропускания
;
в полосах задерживания
;
в промежуточных полосах значение
не задано и может быть принято любым в
пределах от 0 до 1.
Так, для ФНЧ
Аппроксимирующие функции имеют вид:
При нечётном N
причём
;
при чётном N
причём
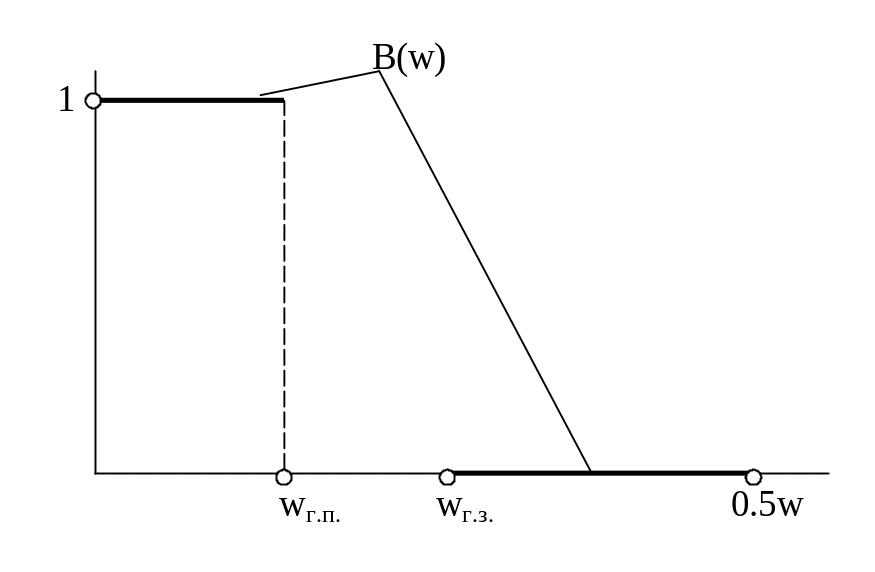
Рис. 1.6.
Методы решения задач аппроксимации тесно связаны с принятыми критериями аппроксимации. В зависимости от использованного критерия их можно разбить на три группы. Первая группа соответствует среднеквадратическому критерию, вторая наилучшему равномерному (чебышевскому) критерию и третья – иным критериям аппроксимации. Первая группа включает методы разложения в ряд Фурье и наименьших квадратов, вторая – алгоритм Ремеза и некоторые другие сравнительно редко используемые алгоритмы. Методы последней группы основаны на интерполяции аппроксимируемой функции и относительно редко используются.
Рассмотрим метод наименьших квадратов.
Этот метод точно соответствует критерию
(1.20) – при заданных величинах
и функциях
и
требуется определить вектор
,
минимизирующий целевую функцию
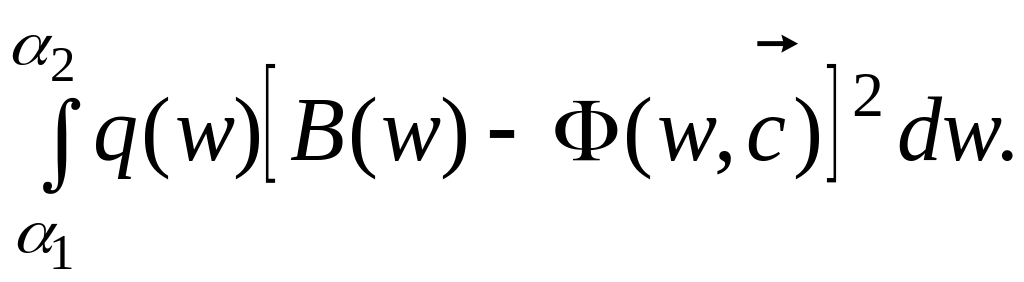(1.20)
Необходимые и достаточные условия минимума (1.19) имеют вид:
(1.21)
и с учётом (1.19) сводятся к системе линейных
алгебраических уравнений относительно
:
,
(1.22)
где
;
;
.
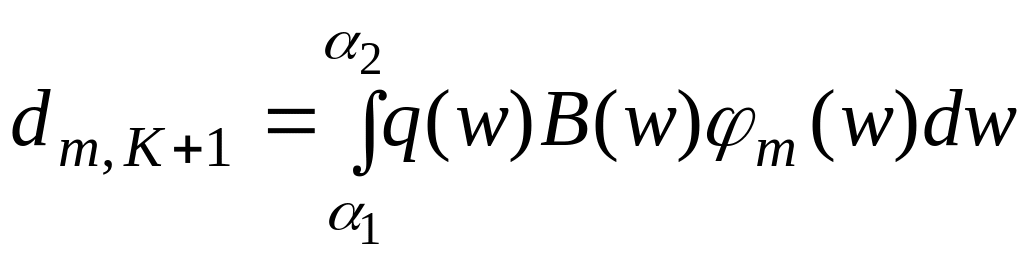При решении задачи аппроксимации можно
оценить её погрешность. Как правило,
погрешностью аппроксимации АЧХ в j-й
полосе пропускания или задерживания
фильтра с граничными частотами
и
называют величину
(1.23)
при .
Для метода наименьших квадратов значение
рассчитывается на ЭВМ методом перебора
значений функции
с шагом
на интервале
.
Максимально допустимое значение
,
при котором
ещё рассчитывается достаточно точно,
определяется выражением (1.23)
,
где N – порядок фильтра.
1.4. Постановка задачи синтеза КИХ-фильтров с булевыми переменными
На практике, при синтезе частотных характеристик НЦФ, наряду с другими конструкциями применяется конструкция НЦФ с коэффициентами передаточной функции, содержащими всего один ненулевой бит. Это приводит к структурам ЦФ без умножителей и с минимальным числом сумматоров.
В общем случае подходы к проектированию НЦФ основаны на аппроксимации заданных амплитудно-частотных характеристик с помощью аппарата Фурье, метода наименьших квадратов, различных способов интерполяции. Однако получаемые коэффициенты будущего фильтра, как правило, не являются целочисленными.
В нашем случае проектируемый ЦФ определяют
N варьируемых параметров Х1, Х2,…, ХN,
которые будем считать точкой в пространстве
размерностью 2N. Примем в качестве вектора
варьируемых параметров
коэффициенты передаточной функции
проектируемого ЦФ, где N - число пар
коэффициентов в НЦФ. Параметры
можно принять целочисленными булевыми
переменными, принимающими значения 0
или 1. Таким образом, учитывается возможное
улучшение требуемых характеристик АЧХ,
вызываемое выставлением какого-либо
коэффициента фильтра в 0. Частота
представляется осью частот, изменяющихся
в диапазоне
,
где
- центральная частота фильтра (для
фильтров нижних и верхних частот
),
- частота дискретизации фильтра.
Частотная характеристика НЦФ с единичными коэффициентами имеет вид:
,
(1.24)
где k - номер коэффициента; - коэффициенты фильтра; N - число пар коэффициентов в НЦФ.
Оптимальность АЧХ проектируемого ЦФ
будем оценивать следующими локальными
критериями: максимальное значение
относительного уровня боковых лепестков
АЧХ найденное в диапазоне частот
,
значения, найденные соответственно на
частоте среза полосы пропускания
и на граничной частоте полосы задерживания
основного лепестка АЧХ.
Подавление боковых лепестков АЧХ в полосе задерживания вычисляется по формуле:
,
где
изменяется от
до
.
Значения АЧХ на заданных уровнях вычисляются следующим образом:
,
,
где - частота среза полосы пропускания, - граничная частота полосы задерживания.
Таким образом, критериальными условиями будут:
,
,
(1.25)
.
АЧХ НЦФ с основными критериальными показателями показана на рис. 1.7.
Рис. 1.7. АЧХ НЦФ с основными критериальными показателями
Рассмотрим задачу поиска условного
экстремума. В качестве целевой функции
выбирается обобщенное в пространстве
Dx относительное значение бокового
лепестка
.
В качестве варьируемых параметров в
рассматриваемом случае возьмем вектор
коэффициентов нерекурсивного цифрового
фильтра
,
компоненты которого
принимают значения 0 или 1. Тогда задача
синтеза может быть сформулирована в
следующем виде: вариацией параметров
,
найти вектор
,
обеспечивающий
,
(1.26)
при
,
(1.27)
.
(1.28)
Таким образом, задача синтеза нерекурсивного
цифрового фильтра, сводится в
рассматриваемом случае к задаче условной
оптимизации (1.26) – (1.28) с целью нахождения
такого вектора коэффициентов фильтра
,
который приводит к оптимальной или
допустимой (по выбранным критериям)
АЧХ. Характерной особенностью этой
задачи является то, что она является
задачей булева программирования и
синтез осуществляется не во временной,
а непосредственно в частотной области.
Для уменьшения размерности вектора
варьируемых параметров учитывалась
симметрия коэффициентов фильтра,
относительно его центра, благодаря
этому число переменных уменьшается
вдвое. Кроме того, возле центра симметрии
НЦФ обычно обязательно присутствует
группа коэффициентов, которую
нецелесообразно включать в число
варьируемых переменных. Полученное
после этого множество компонент вектора
варьируемых переменных
разбивается на
подмножеств (групп):
.
Заметим, что в общем случае
,
а это означает, что некоторые переменные
могут войти в различные подмножества
.
Такая ситуация соответствует случаю,
когда целевая функция обладает высокой
чувствительностью к переменным из
разных групп.