1.3. Операции над множествами. Диаграммы Венна
Для получения новых множеств из уже
существующих используют операции над
множествами. Рассмотрим основные из
них. Пусть рассматриваемые множества
.
1. Дополнением (до U)
множества (обозначается
)
называется множество всех элементов,
не принадлежащих А (но принадлежащих
U): 
.
2. Объединением множеств А и В
(обозначается
)
называется множество, состоящее из всех
тех элементов, которые принадлежат хотя
бы одному из множеств А, В
(входящих в множество А, или В,
или оба). Другие обозначения: А+В,
(или). Таким образом,
.
3. Пересечение множеств А и В
(обозначается
)
называется множество тех элементов,
которые принадлежат и множеству А,
и множеству В. Другие обозначения:
;
(и). Таким образом,
.
4. Разностью множеств А и В
(обозначается
называется множество всех тех элементов
А, которые не принадлежат В:
.
5. Дизъюнктивной суммой (обозначается
;
)
называется множеством элементов входящих
или в А, или в В, но не одновременно
в А и В. Эквивалентно «разделительному»
«или»:
;
иначе
;
.
Пример 1. Пусть А={1, 2, 3} и В={3, 4, 5}.
Тогда
;
={3};
;
.
.
Универсальное множество U
здесь не определено, поэтому, строго
говоря, операции дополнения над
множествами А и В не могут быть
выполнены. Для этого нужно дополнить
условие: пусть U={1,
2, 3, 4, 5}. Тогда :
;
.
Пример 2. Дано: U={1, 2, 3, 4}; A={1, 3, 4}; B={2, 3}; C={1, 4}
Найти: а)
;
б)
;
в)
;
г)
.
Решение:
а)
.
б)
в)
г)
Различные операции с множествами удобно изображать с помощью диаграмм Венна (Эйлера). Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него – каких-нибудь замкнутых фигур (кругов, треугольников и
т. п.), представляющих множества. Результат выделяется штриховкой.
Пусть
А B
Тогда
Замечание 1. Операции объединения,
пересечения и дополнения
часто называют булевыми операциями
над множествами.
Замечание 2. Операции объединения и пересечения в P(U), множестве всех частей множества U, аналогичны операциям сложения и умножения в Z.
1.4. Свойства операций над множествами
Операции над множествами обладают определёнными свойствами и удовлетворяют некоторым соотношениям.
1. Коммутативность операций
и
:
; 
.
2. Ассоциативность операций и :
;
.
3. Законы идемпотентности:
; 
.
4. Законы дистрибутивности:
А;
5. Законы поглощения:
;
6. Законы де Моргана
.
7. Операции с несобственными подмножествами:
,
,
,
,
,
.
8. Инволюция (закон двойного отрицания):
В справедливости данных свойств можно убедиться, например, нарисовав диаграммы Венна для левой и правой частей равенства и проверить, что они совпадают.
Пример: Доказать с помощью диаграмм Венна справедливость соотношения:
(Свойство дистрибутивности 4 операции пересечения относительно объединения).
Из диаграмм видно равенство обеих частей.
Вообще же в теории множеств наиболее часто используются следующие приёмы доказательств:
1. Доказательство равенства соотношений типа X=Y.
2. Доказательство единственности и существования.
3. Доказательство от противного.
а
).
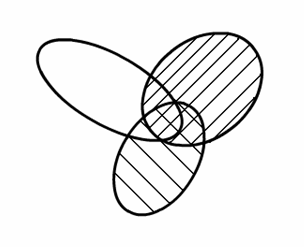
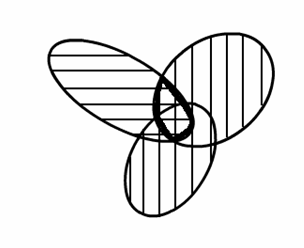A B
A
B
U C U C
(Левая часть)
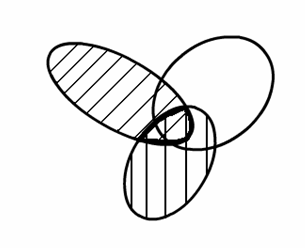
б
).
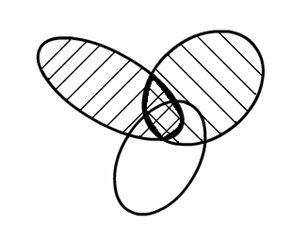A B A
B
U C U C
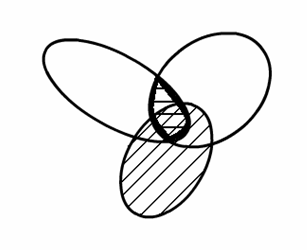A B (Правая
часть)
U C
Пример. Докажем справедливость предыдущего соотношения, используя второе определение равенства X=Y:
Решение. Множества равны, если и .
1. Сначала докажем, что
,
(*)
т. е., что любой элемент а из множества,
заданного левой частью соотношения
(*), принадлежит и правому множеству
соотношения. Пусть
.
Тогда аА
и
аÎ А
и (аÎ В
или аÎ С)
(аÎ А и
аÎ В) или
(аÎ А и аÎ
С) Þ
или
Þ
.
Т. е.
2. Теперь покажем, что
,
т. е. любой элемент из множества, заданного
правой частью (*), принадлежит и множеству,
заданному левой частью.
Пусть
.
Тогда
или
Þ
(аÎ А и аÎ
В) или (аÎ
А и аÎ
С) Þ аÎ
А и (аÎ В
или аÎ С)
Þ аÎ
А и (аÎ В
или аÎ С)
Þ аÎ
А и
Þ
.
Следовательно, .
Таким образом, , ч. т. д.
В качестве следующего примера докажем один из законов де Моргана.
Пример. Доказать
Решение. С одной стороны,
Þ
.
С другой стороны,
.
Так как и , то , ч. т. д.
Утверждение 1. Следующие предположения о произвольных множествах попарно эквивалентны:
1)
2)
Û 3)
Û 4) А\В =
Û 5)
.
Доказательство: 12.
Так как
,
то достаточно показать, что А
В влечёт
.
Но если хА,
то по условию хВ,
следовательно
.
23. Так как
,
то
.
По закону поглощения и закону
коммутативности имеем
.
Тогда
.
3 Þ 4. Пусть
.
Так как
,
то по свойству де Моргана, свойству
ассоциативности, свойству коммутативности
и правилам действия с несобственными
множествами получим:
.
=.
4Þ5. Пусть А\В = ,
т. е.
.
Тогда
.
По закону де Моргана и свойству двойного
отрицания получаем
.
5Þ1. Пусть
и предположим, что не выполняется условие
АВ, т.
е. найдется такой элемент х, что хÎ
А и xÏ
В. Тогда
,
значит,
,
а это противоречит равенству
,
ч. т. д.
Замечание. Пересечение и объединение могут быть определены для любого множества множеств Ai , где индексы i пробегают множество I. По определению
{x| xÎ
Ai
для всех iÎ
I}
(пересечение) -
.
{x| xÎ
Ai
для некоторых iÎ
I}
(объединение) -.
Если I={1, 2, …, n},
то используют записи
или
.