1.10.2 Функции и отображения

Понятие функции является одним из основных в математике. В математическом анализе под функцией чаще всего понимается «числовая» функция, отображающая одно числовое множество в другое. Здесь мы будем рассматривать, прежде всего, функцию, отображающую одно конечное множество объектов в другое конечное множество.

Определение. Пусть А и В конечные множества.

Функцией называется функциональное соответствие.

Если функция  устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип АВ.

Обозначается : АВ.

Таким образом, функция – специальный тип отношения из А в В.

Каждому элементу а из области определения функция  ставит в соответствие элемент b из области значений. Это обозначается (а) = b.

Элемент а – аргумент функции, элемент b – значение функции на а.

Отображением А в В называется всюду определённая функция : АВ.

Образом отображения А в В называется множество (А) всех значений (а), которое оно принимает при всевозможных аА. Образ  является подмножеством множества В.

Отображением А на В называется всюду определённое и при этом сюръективное функциональное соответствие

: АВ.

К специальным отображениям часто относятся понятия оператора и функционала.

Оператор – отображение одного множества на другое, каждое из которых наделено некоторой структурой.

Функционал – отображение произвольного множества Х в множество комплексных или действительных чисел.

Отображением типа АА часто называют преобразованием множества А.

Функции  и g равны, если:

• их области определения – одно и то же множество А,

• для любого аА (а) = g(a).

Таким образом, функции могут быть строго одинаковыми только тогда, когда их области определения и значений совпадают (A₁=A, и B₁=B) .

Если f_A =A, то функция называется тотальной, а если – частичной.

Таблица 1.

Соответствие	Обязательное свойство
	функцио- нальное	всюду определённое	сюръек- тивное
Функция	+	–	–
Отображение А в В	+	+	–
Отображение А на В	+	+	+

Функция называется функцией n аргументов или n-местной функцией. В этом случае принято считать, что функция имеет n аргументов: , где .

Пусть дано соответствие . Тогда соответствие называется обратным к G (обозначается G ^-1), если Н таково, что (b, a)H тогда и только тогда, когда

(а, b)G.

Если соответствие, обратное к функции : АВ, является функциональным, то оно называется функцией, обратной

к  (обозначается f^-1).

Для функции : АВ обратная функция существует только тогда, когда  является взаимно однозначным соответствием между своими областями определения и значений.

1.10.3. Инъекция, сюръекция и биекция

Пусть : АВ.

1, Функция  называется инъективной, или инъекцией, если из в А следует, что в В, т. е., если и . Иными словами, инъекция переводит различные элементы области А в различные элементы области В. Её часто называют взаимно однозначным отображением А в В.

По другому: функция : АВ называется инъективной, или инъекцией, если каждый элемент bB имеет хотя бы один прообраз аА либо вообще не имеет прообраза. Можно видеть, что условие для любого bB или |A||B| определяет инъекцию.

Пример 1. Пусть A={1, 2, 3}; . Функция : АВ инъективна, если .

2. Функция называется сюръективной, или сюръекцией, если её образ совпадает со всей областью В, т. е. для каждого bB существует хотя бы один элемент аА такой, что (а)=b. Сюръекции часто обозначаются так и называется отображением А на (все) В.

Т. е. .

Иначе: функция : АВ называется сюръективной или сюръекцией, если любой элемент bB есть образ по крайней мере одного аА. Условие для любого bB или |x||y| характеризует сюръекцию.

Пример 2. Пусть A={1, 2, 3,4}; . Функция : АВ сюръективна, если . Та же функция Ψ:{1, 2, 3} с условием

(1)= (3)=y₁ ; (2)= (4)=y₃ не является сюръективной.

2. Функция называется биективной, или биекцией, если она является одновременно инъекцией и сюръекцией. Иными словами, биективное отображение взаимно однозначно и является отображением на ( ).

Для биективной функции для любого bB или |x|=|y|.

Пример 3: Пусть A={1, 2, 3}; .

Функция : АВ биективна, если

Биективная функция определяет взаимно однозначноесоответствие между множествами А и В.

Схематически различные виды отношений изображены на рис.8.

Р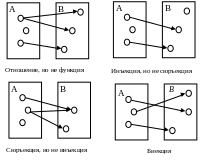 ис.8.

Если между множествами А и В можно установить взаимно однозначное соответствие, то А называется эквивалентным множеству В. Установление взаимно однозначного соответствия между множествами играет важную роль. Так, определение числа элементов конечного множества Х, т. е. установление равенства |x|=n при некотором n, фактически сводится к отыскиванию некоторого взаимно однозначного соответствия между множествами Х и N={1, 2, 3, …, n}. Множества, равномощные N, называются счётными.

Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие, т. е. эквивалентные множества являются равномощными.

Пример 4. Биекцией между множеством натуральных чисел N={0, 1, 2, …} и множеством целых чисел

Z{0, ±1, ±2, …} является функция : NZ, для которой

Таким образом, обратная функция существует для биекции

П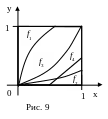 ример 5. На рис.9 графически показаны функции :

f_i:[0, 1][0, 1], i{1, 2, 3, 4}.

Функция f₁ сюръективна, но не инъективна;

Функция f₂ инъективна, но не сюръективна;

Функция f₃ биективна, а функция f₄ не инъективна и не сюръективна

Пример 2. Рассмотрим три функции

f_i:: RR, i=1, 2, 3:

1. функция f₁(x)= e^x инъективна, но не сюръективна;

2. функция f₂(x)= xsinx сюръективна, но не инъективна;

3. функция f₃(x)= 2x-1 биективна.

Пример 6. Среди функций из Z в Z отображение биективно; отображение инъективно, но не сюръективно, а отображение не инъективно и не сюръективно (почему?).