
- •1. Элементы теории множеств
- •1.1 Множества. Основные понятия
- •1.2. Способы задания множеств
- •1.3. Операции над множествами. Диаграммы Венна
- •1.4. Свойства операций над множествами
- •1.5. Прямое (декартово) произведение множеств
- •1.6 Разбиения и покрытия
- •1.7. Замечание о мощности некоторых множеств
- •1.8 Представление множеств в эвм
- •1.9. Отношения
- •1.9.1.Определения
- •1.9.2 Бинарные отношения
- •1.9.3. Способы задания бинарных отношений
- •1.9.4 Свойства бинарных отношений
- •1.9.5. Отношение эквивалентности
- •1.9.5. Отношение порядка
- •1.9.6.1. Минимальные и максимальные элементы множества
- •1.9.6.2. Диаграммы Хассе
- •1.9.6.3. Принцип двойственности
- •1.9.7. Представление отношений в эвм
- •1.10. Соответствия. Функции. Операции. Отображения
- •1.10.1. Соответствия и их свойства
- •1.10.2 Функции и отображения
- •1.10.3. Инъекция, сюръекция и биекция
- •1.10.4. Композиция и суперпозиция функций. Способы задания функций
- •1.10.5. Представление функций в эвм
- •1.10.6. Операции
- •1.10.6.1. Способы задания операций
- •1.11. Алгебраические структуры
- •1.11.2. Замыкание и подалгебры
- •1.11.3. Гомоморфизм и изоморфизм
- •1.11.4. Алгебры с одной бинарной операцией
- •1.11.5. Алгебры с двумя бинарными операциями
- •1.11.6.Решетки
- •1.11.7. Булевы алгебры
- •2. Элементы математической логики и булевы функции
- •2.1. Операции над высказываниями
- •2.2. Логические операции (логические связки)
- •2.3. Элементарные булевы функции
- •2.3.1. Функции алгебры логики
- •2.3.2. Равносильность функций. Существенные и несущественные переменные
- •2.3.3. Реализация функций формулами. Суперпозиция функций
- •2.3.4. Подстановки и замены
- •2.3.5. Принцип двойственности
- •2.3.6. Нормальные формы в логике высказываний
- •2.3.6.1. Разложение булевых функций по переменным. Дизъюнктивно-нормалльная форма (днф)
- •2.3.6.2. Совершенная дизъюнктивная нормальная форма
- •2.3.7. Арифметические операции в алгебре логики. Полиномы Жегалкина
- •2.3.8. Монотонные функции алгебры логики
- •2.3.9. Функционально замкнутые классы
- •2.4. Полнота системы булевых функций. Теорема
- •2.5. Элементы логике предикатов
- •2.5.1. Определение предиката
- •2.5.2. Кванторы. Формулы логики предикатов
- •2.5.3. Равносильность формул
- •2.5.4. Предикаты на конечных областях. Логика одноместных предикатов
- •2.6. Операции над предикатами и кванторами
- •2.7. Построение доказательств в логике предикатов
- •1.6.2. Разбор решений задач по логике предикатов
- •1. Элементы теории множеств 3
- •1.1 Множества. Основные понятия 3
- •2.6. Операции над предикатами и кванторами 137
- •394026 Воронеж, Московский просп., 14
1.11.3. Гомоморфизм и изоморфизм
Рассмотрим специальные отношения для
алгебр. Пусть между множествами А
и В установлено соответствие G
– отображение А в В, т.е.
![]() .
Это означает, что каждому элементу
.
Это означает, что каждому элементу
![]() поставлен в соответствие G
единственный элемент
поставлен в соответствие G
единственный элемент
![]() из B, т.е.
из B, т.е.
![]() .
Пусть так же на множестве А задана
операция
,
на множестве B – операция
.
Пусть так же на множестве А задана
операция
,
на множестве B – операция
![]() ,
обе одинаковой арности, например, обе
бинарные. (Рассматриваются алгебры
одинакового типа, так как алгебры с
различными типами имеют различное
строение.)
,
обе одинаковой арности, например, обе
бинарные. (Рассматриваются алгебры
одинакового типа, так как алгебры с
различными типами имеют различное
строение.)
Т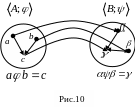 аким
образом,
аким
образом,
![]() и
и
![]() .
.
Следовательно, имеем две алгебры
одинакового типа:
![]() .
.
Отображение
называется
гомоморфизмом алгебры
![]() в
алгебру
в
алгебру
![]() ,
если выполняется условие:
,
если выполняется условие:
![]() (1)
(1)
Условие гомоморфизма (1) требует (см.
рис.10), чтобы отображение G
результата
![]() выполнения на множестве А операции
над элементами a и b,
то есть
выполнения на множестве А операции
над элементами a и b,
то есть
![]() совпадало с результатом выполнения на
множестве B операции
над отображениями этих элементов, т.е.
над
и
совпадало с результатом выполнения на
множестве B операции
над отображениями этих элементов, т.е.
над
и
![]() .
.
Д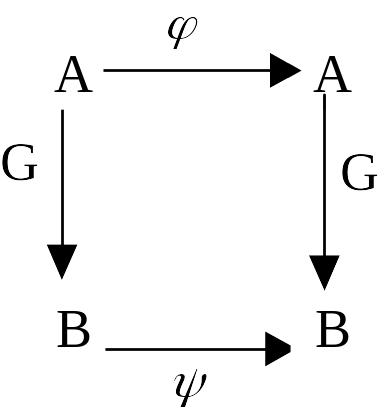 ействие
этих функций можно изобразить с помощью
следующей диаграммы.
ействие
этих функций можно изобразить с помощью
следующей диаграммы.
Пусть G
– гомоморфизм. Тогда если взять конкретные
значения
![]() и двигаться двумя различными путями на
диаграмме , то получится один и тот же
элемент
и двигаться двумя различными путями на
диаграмме , то получится один и тот же
элемент
![]() ,
так как
,
так как
![]()
Проверка условия гомоморфизма заключена в следующем. В соответствии с левой частью условия (1) сначала над элементами a и b из А, должна быть выполнена операция , а затем ее результат отображается из А в множество В.
В соответствии с правой частью условия
(1) требуется сначала выполнить отображения
элементов a и b
из множества А в В, т.е. найти
и
,
а затем над
и
![]() выполнить операцию
(заданную на множестве В), т.е.
выполнить операцию
(заданную на множестве В), т.е.
![]() или
или
![]() .
.
Условия (1) будет выполнено, если результат
отображения элемента
![]() из
А в В совпадает с элементом
из
А в В совпадает с элементом
![]() из множества В, т.е. если
из множества В, т.е. если
![]() .
.
Аналогично вводится понятие гомоморфизма для произвольной арности операции .
Пусть
![]() и
и
![]() - две алгебры одинакового типа. Если
существует функция (соответствие)
- две алгебры одинакового типа. Если
существует функция (соответствие)
![]() такая
что,
такая
что,
![]() ,
то говорят, что
,
то говорят, что
![]() - гомоморфизм из алгебры
- гомоморфизм из алгебры
![]() в алгебру
в алгебру
![]() .
(соответствия типа (1) выполняются для
каждой пары операций
.
(соответствия типа (1) выполняются для
каждой пары операций
![]() ).
).
Если при этом отображение
![]() является
взаимно однозначным соответствием, оно
называется изоморфизмом алгебры
является
взаимно однозначным соответствием, оно
называется изоморфизмом алгебры
![]() на алгебру
на алгебру
![]() .
В этом случае существует и обратное
отображение
.
В этом случае существует и обратное
отображение
![]() ,
так же взаимно однозначные:
,
так же взаимно однозначные:
![]()
Таким образом, гомоморфизм, который является биекцией, называется изоморфизмом.
Отображение
![]() - это в свою очередь, изоморфизм В
на А.
- это в свою очередь, изоморфизм В
на А.
Теорема: Если изоморфизм, то тоже
изоморфизм (без док-ва).
Если G:A→B
– изоморфизм, то алгебры
и
![]() называют изоморфными и обозначают :
называют изоморфными и обозначают :
![]() .
.
В силу взаимной однозначности соответствия G:A→B при изоморфизме (биекция), мощности основных множеств изоморфных алгебр равны. Поэтому проверка алгебр на изоморфизм сводится к проверке условия гомоморфизма для каждой пары операций и установления взаимной однозначности соответствия G (равной мощности множеств А и В).
Теорема. Отношение изоморфизма на множестве однотипных алгебр является эквивалентностью.
Доказательство:
1. Рефлексивность:
![]() ,
G = I
(I – тождественное
отображение)
,
G = I
(I – тождественное
отображение)
2. Симметричность:
![]()
3. Транзитивность:
![]()
Аналогично определяется гомоморфизм и изоморфизм множеств с отношениями моделей <A;R1,R2,...Rn> и <B,R1′1,R′2,...R′n>. Понятие гомоморфизма и изоморфизма для алгебраических структур вводится аналогично тому, как это сделано для алгебр и моделей. При этом должны выполняться условия сохранения и операций, и отношений.
Понятие изоморфизма – одно из важнейших понятий в современной математике, обеспечивающих применимость алгебраических методов в различных областях. Оказывается, что достаточно установить некоторое свойство в одной алгебре, и оно автоматически распространяется на все изоморфные алгебры.
Например, любое эквивалентное соотношение в алгебре Ã сохраняется в любой изоморфной ей алгебре Ã′. Это позволяет, получив такие соотношения в алгебре Ã, автоматически распространив их на все алгебры, изоморфные Ã.
В частности, изоморфизм сохраняет свойства, ассоциативности, коммутативности и дистрибутивности операций, а также все свойства отношений.
Пример 1. Пусть Zn – множество всех целых чисел, Z2n – множество всех четных целых чисел. Изоморфны ли следующие алгебры:
à = (Zn;+ ) и = (Z2n;+ ) при отображении
G: n→2n
à = (Zn;+ ) и = (Zn;+ ) при отображении
G: n→(-n)
à = (Zn;
 ) и
= (Zn;
) при отображении
) и
= (Zn;
) при отображении
G: n→(-n)
à = (Zn; ) и = (Z2n; ) при отображении G: n→2n
à = (Zn;
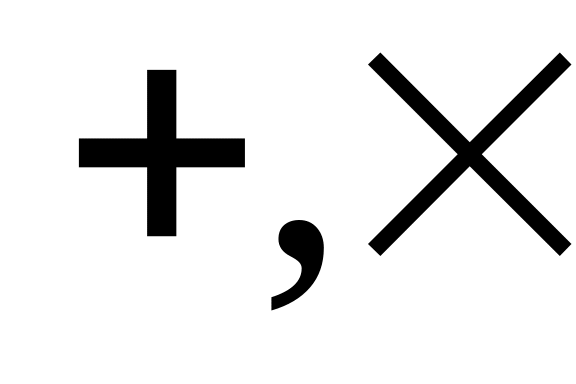 ) и
= (Z2n;
) при отображении
) и
= (Z2n;
) при отображении
G: n→2n
где – операции арифметического сложения и умножения соответственно.
Решение.
а)
Условие гомоморфизма для алгебр Ã = (Zn;+) и
= (Zzn;+ ) проиллюстрировано на рис.11, где изображены два множества Zn и Z2n и в Zn выделены произвольные два элемента a и b.
В соответствии с левой частью условия
(1) гомоморфизма для бинарных операций
выполним над
![]() и
и
![]() операцию сложения + алгебры
и отобразим результат
операцию сложения + алгебры
и отобразим результат
![]() в
множество
в
множество
![]() алгебры
.
алгебры
.
<Zn;+> <Z2n;+>


рис.11.
G(c) = G(a) + G(b) -?
При заданном отображении
![]() элементу с множества
элементу с множества
![]() соответствует элемент 2с множества
,
т.е. левая часть условия (1) примет вид:
соответствует элемент 2с множества
,
т.е. левая часть условия (1) примет вид:
![]() .
.
Правая часть условия (1) требует сначала
отображения элементов
![]() в
множество
.
Это дает
в
множество
.
Это дает
![]() ;
;
![]() .
Затем осуществим над полученными
отображениями операцию сложения (+)
алгебры
.
правая часть условия (1) примет вид:
.
Затем осуществим над полученными
отображениями операцию сложения (+)
алгебры
.
правая часть условия (1) примет вид:
![]()
Таким образом, условие гомоморфизма
(1) для алгебр
![]() при отображении
имеет вид:
при отображении
имеет вид:
![]() ,
т.е.
,
т.е.
![]()
Так как данные условия выполняются, алгебры и гомоморфны, а в силу взаимной однозначности отображения , они и изоморфны.
б) Отображение
![]() для алгебр
для алгебр
![]() и
и
![]() является изоморфизмом. Действительно,
условие (1) имеет вид
является изоморфизмом. Действительно,
условие (1) имеет вид
![]()
и, кроме того, отображение
(каждому целому числу
![]() в алгебре
соответствует
то же самое число, но с противоположным
знаком (-n) в
алгебре
)
– взаимно однозначно.
в алгебре
соответствует
то же самое число, но с противоположным
знаком (-n) в
алгебре
)
– взаимно однозначно.
в) Отображение
для алгебр
![]() и
и
![]() не является ни изоморфизмом, ни
гомоморфизмом, так как не выполняется
условие (1) гомоморфизма.
не является ни изоморфизмом, ни
гомоморфизмом, так как не выполняется
условие (1) гомоморфизма.
![]()
г) Алгебры
и
![]() не являются гомоморфными, а значит, и
изоморфными при отображении
,
поскольку для них не выполняется условие
(1):
не являются гомоморфными, а значит, и
изоморфными при отображении
,
поскольку для них не выполняется условие
(1):
![]()
д) Для алгебр
![]() и
и
![]() при отображении
условие гомоморфизма выполняется для
операций сложения:
и
не выполняется для операций умножения:
при отображении
условие гомоморфизма выполняется для
операций сложения:
и
не выполняется для операций умножения:
![]() ,
поэтому алгебры
и
не являются гомоморфными.
,
поэтому алгебры
и
не являются гомоморфными.
Пример 2.
Гомоморфны (изоморфны) ли алгебры
![]() и
и
![]() при отображении
при отображении
![]() (
(![]() - множества действительных и положительных
действительных чисел соответственно)?
- множества действительных и положительных
действительных чисел соответственно)?
Решение:
Алгебры и изоморфны при заданном отображении , так как выполняется условие (1) :
![]()
и отображение взаимно однозначно. В частности, этот принцип (изоморфизм указанных алгебр при данном отображении) используется при вычислениях с помощью логарифмической линейки.
Пример 3.
Изоморфны ли булевы алгебры множеств
![]() и
и
![]() ,
образованные двумя различными множествами
,
образованные двумя различными множествами
![]() и
и
![]() одинаковой
мощности?
одинаковой
мощности?
Решение:
Алгебры
и
,
где
![]() ,
изоморфны, так как операции у них просто
одинаковы, а отображением G
может служить любое взаимно однозначное
соответствие между
и
.
,
изоморфны, так как операции у них просто
одинаковы, а отображением G
может служить любое взаимно однозначное
соответствие между
и
.
Например, множества
![]() и
и
![]() одинаковой мощности,
одинаковой мощности,
![]() .
Тогда отображение
.
Тогда отображение
![]() задает изоморфизм алгебр.
задает изоморфизм алгебр.
Пример 4.
Пусть алгебры
![]() и
и
![]() ,
где
,
где
![]() - сложение по модулю 3 и
- сложение по модулю 3 и
![]() ,
и отображение
,
и отображение
![]() определено следующим образом:
определено следующим образом:
![]() равно остатку от деления n
на 3. Т.е., если n=3a+b,
где b<3, то G(n)=b.
равно остатку от деления n
на 3. Т.е., если n=3a+b,
где b<3, то G(n)=b.
Например,
![]() ;
;
![]() и т.д.
и т.д.
Гомоморфны (изоморфны) ли алгебры и ?.
Решение.
Пусть
![]() и
и
![]() - два произвольных натуральных числа
из N; b1,b2<3.
Проверим условие (1):
- два произвольных натуральных числа
из N; b1,b2<3.
Проверим условие (1):
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Очевидно, это условие выполняется. Например, пусть n1=56, n2=37. Тогда 56=318+2; 37=312+1. Подставив в полученное условие гомоморфизма, убедимся в его выполнимости:
![]() ,
0=0.
,
0=0.
Таким образом, отображение G
– гомоморфизм. Но оно не является
изоморфизмом, так как нет взаимной
однозначности для
![]() .
.
Этот пример показывает, что возможен гомоморфизм бесконечной алгебры (алгебры с бесконечным основным множеством) в конечную алгебру.
