8. Оптимальность по Парето

При решении практических задач нередко приходится иметь дело с ситуациями, когда необходимо одновременное выполнение нескольких условий (критериев).

Множество Парето

Рассмотрим на плоскости (U,V) множество Ω (рис. 2).

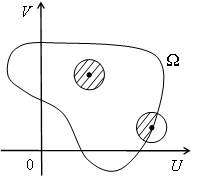
Рис. 2.

Каждая его точка обладает одним из следующих свойств: либо все точки, ближайшие к ней, принадлежат множеству Ω (такая точка называется внутренней точкой множества Ω), либо сколь угодно близко от неё расположены как точки множества Ω, так и точки, множеству Ω не принадлежащие (такие точки множеству Ω называются граничными точками множества Ω). Множество всех граничных точек множества называется его границей. Обозначение: ∂Ω. Граничная точка может как принадлежать, так и не принадлежать множеству Ω. Будем рассматривать только такие множества, которым принадлежат все точки границы.

Точки множества Ω можно разбить на три класса:

к первому классу относятся точки, которые можно сдвинуть так, чтобы одновременно увеличились обе координаты и при этом точки остались в множестве Ω (в этот класс попадают точки все внутренние точки множества Ω и часть его граничных точек);

второй класс образуют точки, перемещением которых по множеству Ω можно увеличить только одну из координат при сохранении значения второй (вертикальный отрезок AB и горизонтальный PQ на границе множества Ω) (рис. 3);

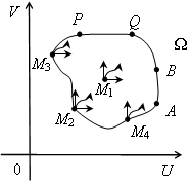
Рис. 3.

в третий класс попадут точки, перемещением которых по множеству Ω способно лишь уменьшить хотя бы одну из координат (дуга BQ границы ∂Ω) (рис. 4).

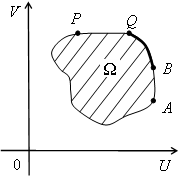
Рис. 4.

Множество точек третьего класса называется границей (множеством) Парето данного множества Ω. Говоря нестрого, граница Парето множества Ω – это точки, из которых нельзя сдвинуться на «север», «восток» либо «северо-восток», оставаясь в том же множестве Ω.

Постановка задачи

Пусть на плоскости (x,y) задано множество ω (рис. 5) и в каждой точке этого множества определены две непрерывные функции U = Φ(x,y) и V = Ψ(x,y).

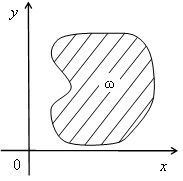
Рис. 5.

Рассмотрим следующую задачу. На множестве ω найти точку (x⁰,y⁰), в которой и , В исходной постановке задача, вообще говоря, неразрешима. Следовательно, нужно искать какое-то компромиссное решение.

Метод идеальной точки

Метод идеальной точки состоит в отыскании на границе Парето точки, ближайшей к точке утопии, задаваемой лицом, принимающим решение (ЛПР). Обычно ЛПР формулирует цель в виде желаемых значений показателей, и часто в качестве координат целевой точки выбирается сочетание наилучших значений всех критериев (обычно эта точка не реализуется при заданных ограничениях, поэтому её и называют точкой утопии).

Пусть на множестве ω плоскости (x,y), определяемом системой неравенств

заданы две линейные функции:

(1)

Требуется найти решение задачи и .

Множество ω представляет собой пятиугольник (рис. 6), вершины которого имеют следующие координаты А(0,0), B(0,2), C(2,2), D(4,1), E(4,0).

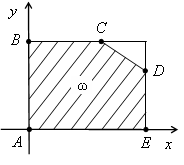
Рис. 6.

В силу линейности критериев U и V пятиугольник ABCDE переходит в пятиугольник A^*B^*C^*D^*E^* (рис. 7), кординаты вершин которого вычисляются по формулам (1):

А^*(0,0), B^*(0,2), C^*(2,2), D^*(4,1), E^*(4,0).

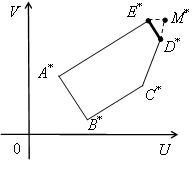
Рис. 7.

Находим границу Парето. Это отрезок D^*E^*. Точка утопии M^*(7,10) считается заданной (её координаты суть наибольшие значения U и V).

Требуется найти на множестве Парето точку, ближайшую к точке утопии M^*. Из рисунка видно, что искомая точка должна лежать на отрезке D^*E^*. Проведём через точки D^* и E^*прямую. Пусть - её уравнение. Чтобы отыскать конкретные значения параметров и , подставим в него координаты обеих точек – и D^*, и E^*. Получим

Вычитая из первого равенства второе, после простых преобразований придём к соотношению

откуда Положим Тогда и U + V =16 – искомое уравнение прямой. По условию задачи нам нужно определить на этой прямой точку М⁰(U⁰,V⁰), расстояние которой от точки M^*(7,10) минимально, т.е. решить экстремальную задачу: Так как U = 16 – V, то последнее соотношение можно переписать в виде

Возводя в квадрат и приводя подобные, получаем, что

Это уравнение описывает параболу с вершиной (координата находится из условия равенству нулю производной z' = 4V – 38. Тогда

Идеальная точка находится на расстоянии от точки утопии M^*(7,10) (рис. 8).

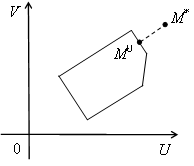
Рис. 8.

Соответствующие значения x и y легко находятся из системы линейных уравнений

Имеем:

Замечание. Мы рассмотрели задачу, в которой , . На практике часто встречаются случаи, когда требования выглядят по-иному -

,

или

, .

Такие задачи решают, учитывая, что функция достигает наибольшего значения в тех точках, где функция принимает наименьшее значение, и наоборот. Иными словами, условия и равносильны. Поэтому, поменяв в случае необходимости знак у критерия на противоположный, мы можем свести любую двухкритериальную задачу к уже рассмотренной: , . Рассмотрим соответствующий пример.

Пусть на множестве

(рис. 9) заданы две линейные функции:

(2)

Требуется найти решение задачи

, (3)

при условии, что точка утопии M^* имеет координаты (2, -2).

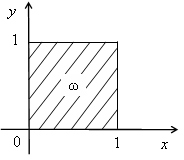
Рис. 9.

Введём новую функцию

. (4)

Тогда требование (3) можно записать так:

, .

Соответственно изменится и точка утопии - N^*(2,2).

Функции и линейны и преобразуют квадрат в параллелограмм (рис. 10), при этом вершины квадрата (0,0), (1,0), (1,1), (0,1) переходят в вершины параллелограмма (0,1), (2,0), (2,1), (0,2).

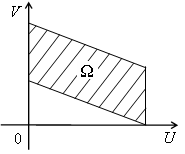
Рис. 10.

Множество Парето образуют точки отрезка с концами A(0,2) и B(2,1) (рис. 11).

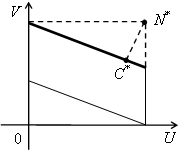
Рис. 11.

Проведём через эти точки прямую и найдём коэффициенты уравнения . Подставляя в него координаты точек A и B, получаем, что , . Положим Тогда и Тем самым уравнение искомой прямой имеет вид U + 2W = 4. Пусть C^*(U,V) - точка этой прямой, ближайшая к точке N^*(2,2). Это означает, что должно выполняться условие: Так как U = 4 – 2W, то оно принимает следующий вид:

Чтобы найти минимальное значение функции ,

приравняем нулю производную. Имеем: z' = 10W – 12 = 0. Отсюда Соответствующие значения x и y находятся из уравнений (см. (2))

откуда

Расстояние от найденной точки до точки утопии N^*(2,2) равно .

Ответ: идеальная точка находится от заданной точки утопии M^*(2,-2) на расстоянии .