Принцип доминирования
В ряде случаев анализ платёжной матрицы обнаруживает, что некоторые чистые стратегии не могут внести никакого вклада в искомые оптимальные смешанные стратегии. Отбрасывание подобных стратегий позволяет заменить первоначальную матрицу на матрицу выигрышей меньших размеров.
Определение 1.
Будем говорить, что вектор-строка а =
(а1, , аl)
доминирует вектор-строку b = (b1,
, bl),
если
.
Будем говорить о строгом
доминировании, если все нестрогие
неравенства ≥ заменены на строгие >.
Замечание. Доминирование возможно даже в случае равенства векторов а и b.
Определение 2.
Для векторов
,
евклидова пространства и чисел
,
,
линейная комбинация
называется выпуклой комбинацией
векторов
с коэффициентами
.
Теорема о доминировании строк.
Пусть некоторая строка матрицы А доминируется выпуклой комбинацией остальных строк. Тогда эта строка входит с нулевой вероятностью в некоторую оптимальную смешанную стратегию первого игрока. Если указанное доминирование строгое, то эта строка входит с нулевой вероятностью в любую смешанную стратегию первого игрока. Доминируемые строки можно вычеркнуть из матрицы игры.
Замечание. При исключении строго доминируемых строк оптимальные смешанные стратегии первого игрока сохраняются. При нестрогом доминировании некоторые из оптимальных стратегий могут быть потеряны. Однако, цена игры не изменится и по усечённой матрице может быть найдена хотя бы одна пара оптимальных смешанных стратегий.
Определение 3.
Будем говорить, что вектор-столбец а =
(а1, , аl)
доминирует вектор-столбец b =
(b1, ,
bl),
если
.
Будем говорить о строгом
доминировании, если все нестрогие
неравенства ≤ заменены на строгие <.
Теорема о доминировании столбцов.
Пусть некоторый столбец матрицы А доминируется выпуклой комбинацией остальных столбцов. Тогда этот столбец входит с нулевой вероятностью в некоторую оптимальную смешанную стратегию второго игрока. Если указанное доминирование строгое, то этот столбец входит с нулевой вероятностью в любую оптимальную смешанную стратегию второго игрока. Доминирующие столбцы можно вычеркнуть из матрицы игры.
Примеры.
Рассмотрим игру с матрицей
.
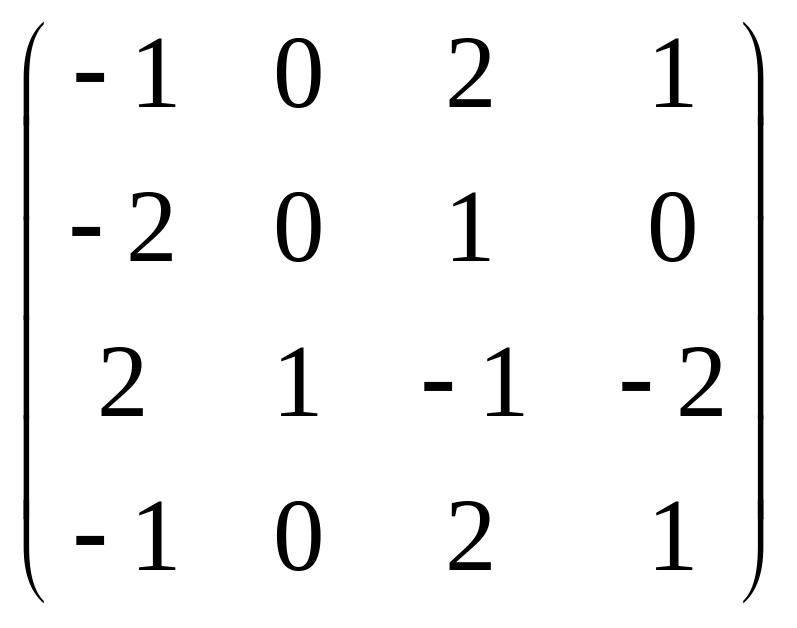Сравнивая строки матрицы, видим, что первая строка совпадает с четвёртой строкой, или, что тоже, стратегия А4 дублирует стратегию А1. Тем самым, одну из этих строк можно вычеркнуть, не нанося ущерба решению:
.
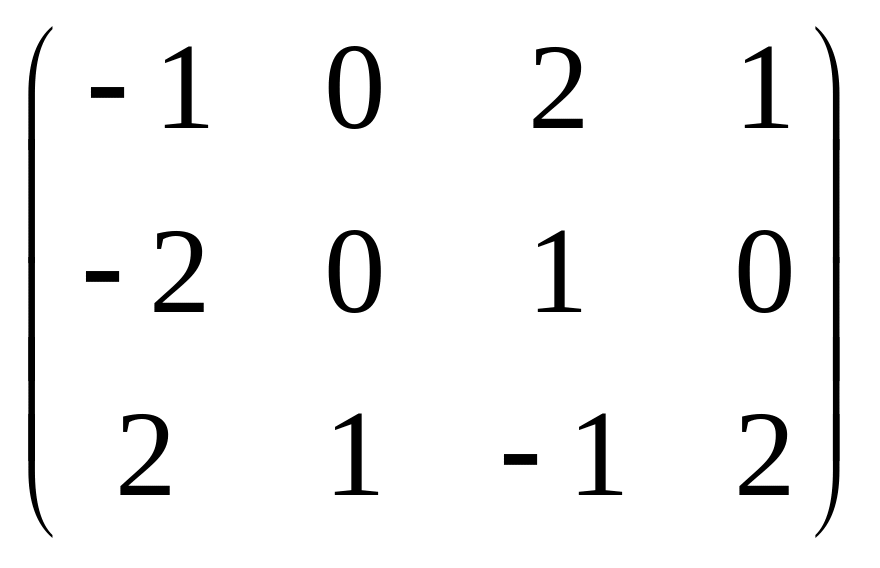Поэлементно сравнивая первую и вторую строки, замечаем, что первая строка доминирует вторую строку, или, что тоже, стратегия А1 доминирует стратегию А2. Это вновь позволяет уменьшить число строк матрицы:
.
Замечая, что четвёртый столбец полученной матрицы доминирует её третий столбец, и, вычёркивая этот последний столбец, приходим к игре с 2×3 матрицей:
.
Рис. 15.
= max (-1, -2) = -1;
= min (2, 1, 1) = 1.
-1 ≤ v ≤ 1.
;
;
;
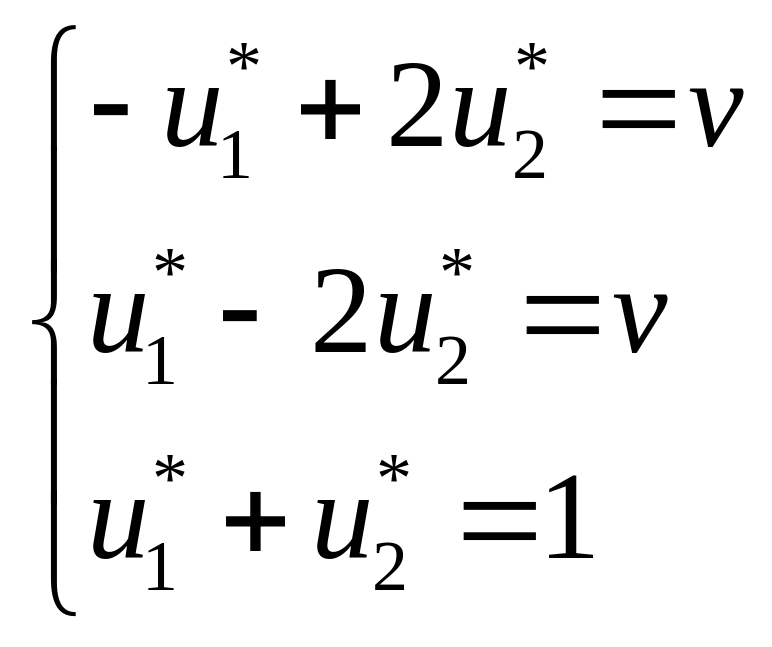
v
=
.
.
.
.
.
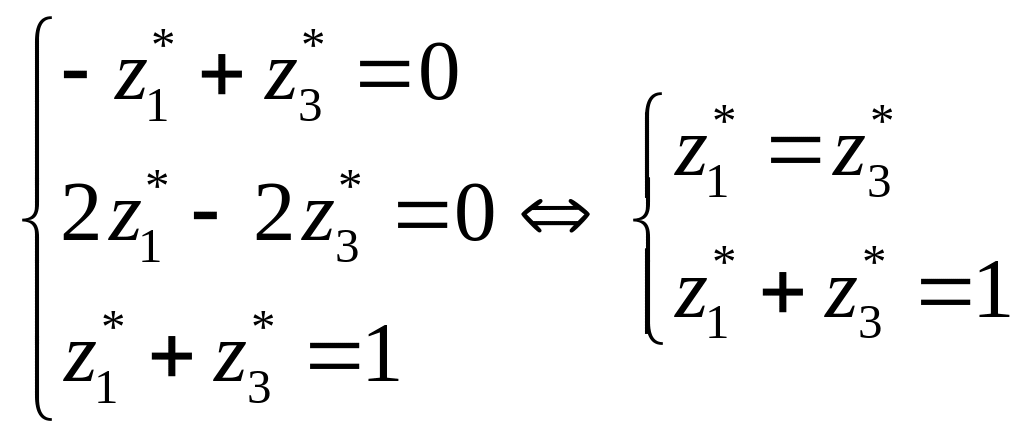
Возвращаясь
к исходной 4×4 игре, получаем окончательный
ответ:
;
;
v
=
.
Решить игру с матрицей
.
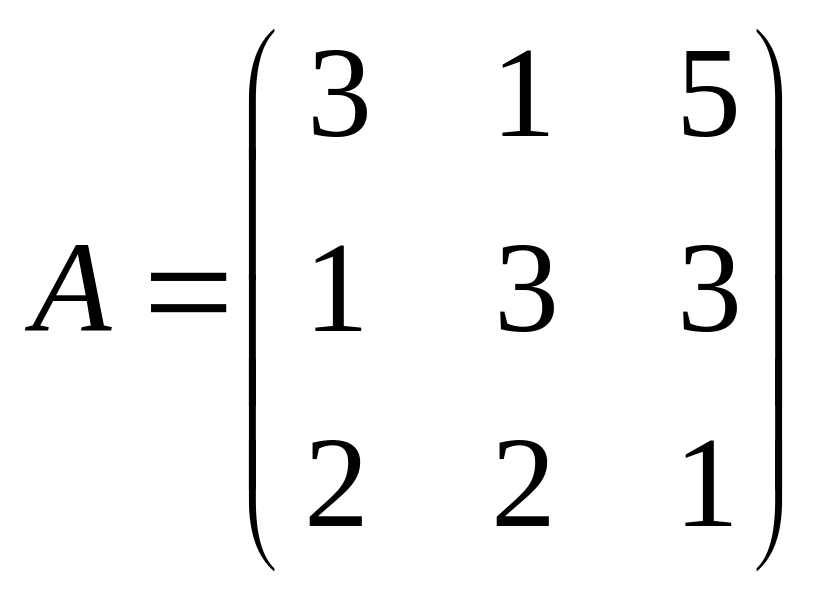Решение.
Здесь полусумма первых двух строк доминирует третью строку и её можно вычеркнуть. Получим матрицу:
.
В ней второй столбец доминирует третий и его можно вычеркнуть. Получим циклическую матрицу:
.
= max (1, 1) = 1;
= min (3, 3) = 3.
1
≤ v ≤ 3
Рис. 16.
;
;
;
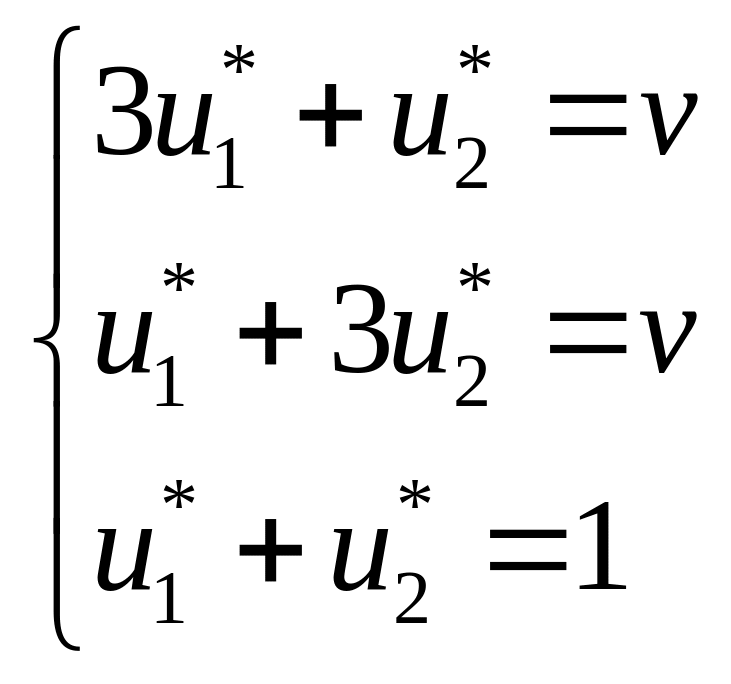
v
=
.
.
; ;
.
.
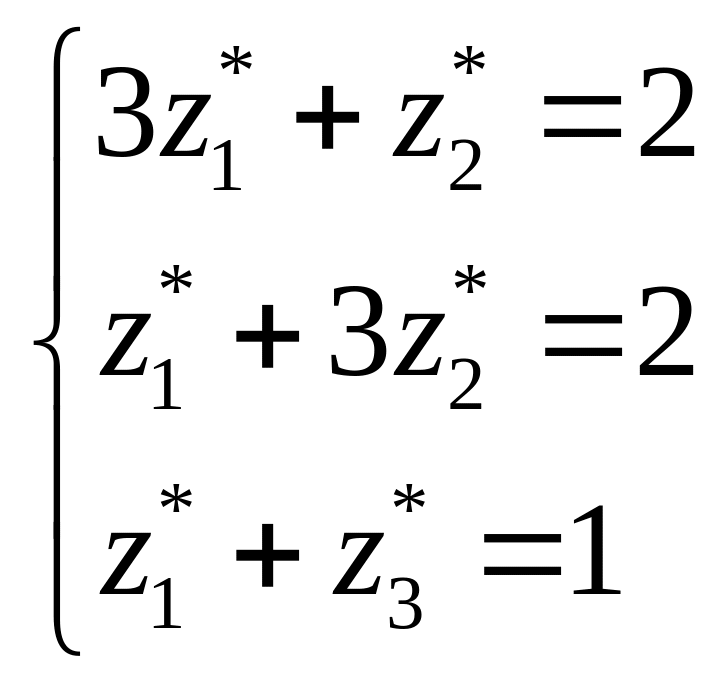
Возвращаясь
к исходной 3×3 игре, получим:
;
;
v
=
.
Решить игру с матрицей:
.
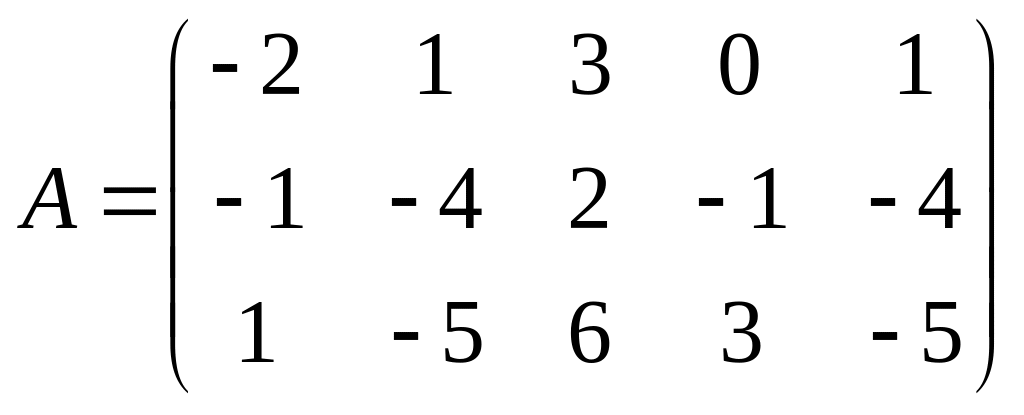Решение.
В данной матрице второй и пятый столбцы одинаковы и один из них, например, пятый, можно удалить. В оставшейся матрице третий столбец строго, а четвёртый столбец нестрого доминируются первым столбцом. Поэтому можно удалить третий и четвёртый столбцы. В результате получим матрицу
.
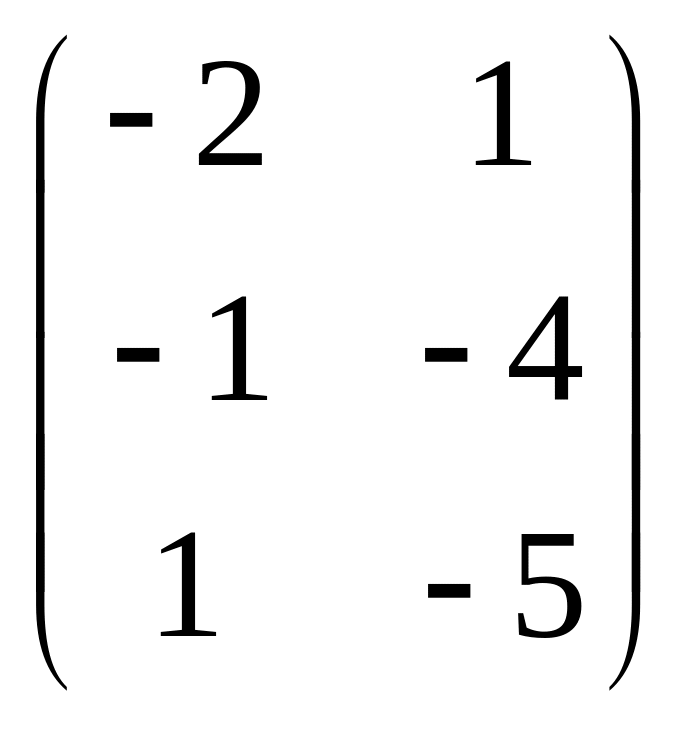Вторая
строка полученной матрицы строго
доминируется выпуклой комбинацией
первой и третьей строк с коэффициентами
и
:
Поэтому нужно отбросить вторую строку. В результате получим матрицу:
.
= max (-2, -5) = -2;
= min (1, 1) = 1.
-2 ≤ v ≤ 1
;
;
;
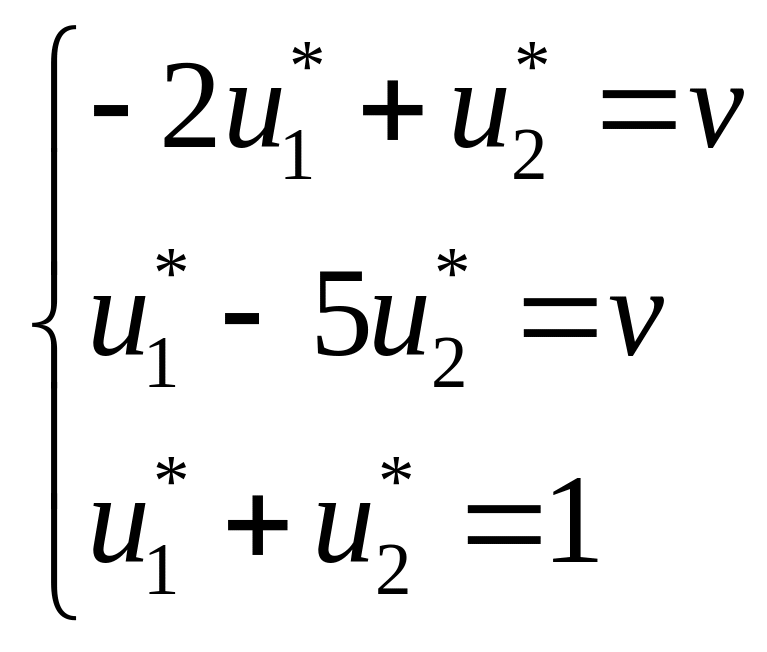
v
=
.
.
;
;
.
.
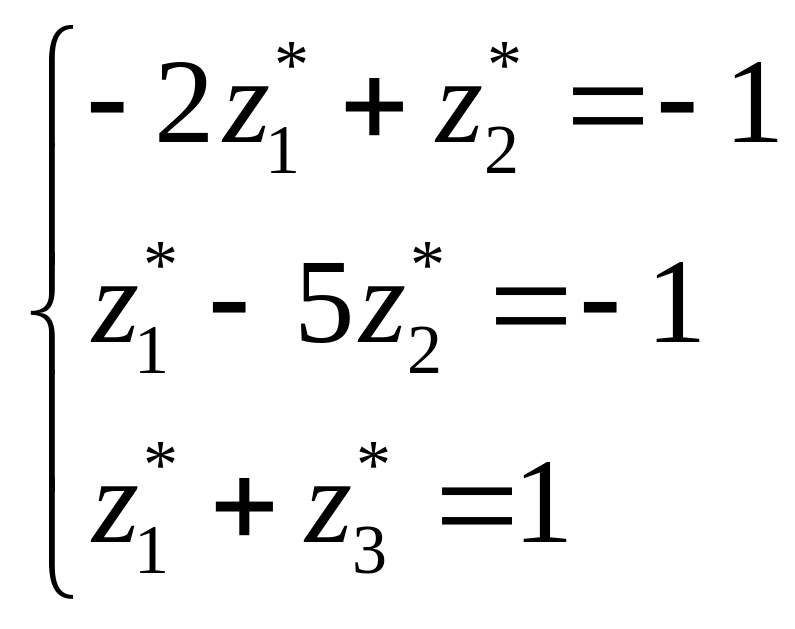
Возвращаясь
к исходной матрице, получим окончательный
результат:
;
;
v
=
.
Поскольку четвёртый столбец матрицы А нестрого доминировался первым столбцом, то могут существовать и другие оптимальные стратегии второго игрока, в которых чистая стратегия В4 будет входить с положительной вероятностью.