4. Метод искусственного базиса

Пусть требуется найти максимум функции

(1)

при условиях

(2)

, (3)

где m<n, и среди векторов

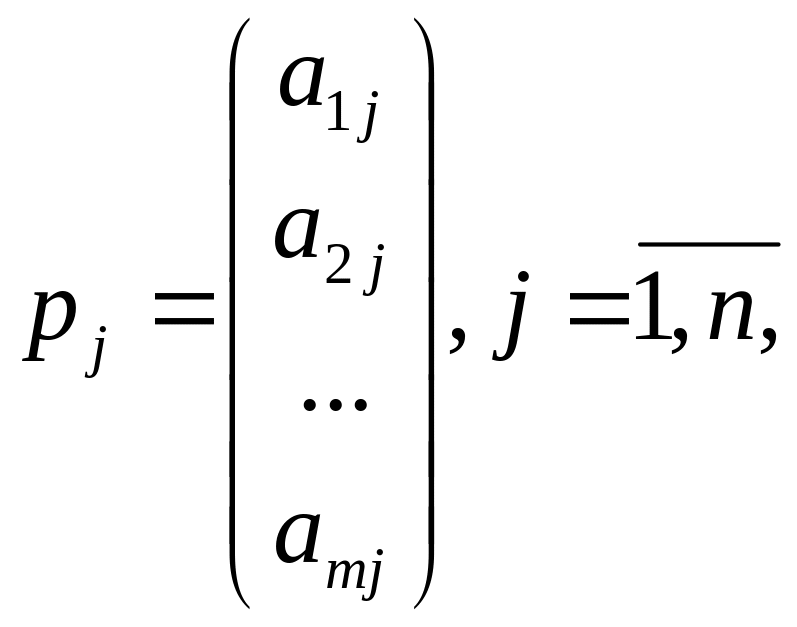
нет m единичных.

Определение. Задача, состоящая в определении максимального значения функции

(4)

при условиях

(5)

(6)

где М - некоторое достаточно большое положительное число, конкретное значение которого обычно не задается, называется расширенной задачей по отношению к задаче (1)-(3).

Расширенная задача имеет опорный план , определяемый системой единичных векторов образующих единичный базис пространства R^m, который называется искусственным базисом. Сами векторы, также, как и переменные называются искусственными.

При опорном плане задачи (4) -(6) , а значения равны Таким образом, и , , состоят из двух частей, одна из которых зависит от М, а другая нет.

После вычисления и , , их значения, а также исходные данные задачи (4)-(6) заносят в таблицу, которая содержит на одну строку больше, чем обычная симплекс - таблица. При этом в (m+2) – ю строку помещают коэффициенты при М, а в (m+1)-ю – слагаемые, не содержащие М.

При переходе от одного опорного плана к другому вводят в базис вектор, соответствующий наибольшему по модулю отрицательному числу (m+2)-ой строке ведут до тех пор пока:

1. либо все искусственные векторы не будут исключены из базиса;

2. либо не все искусственные векторы исключены, но (m+2)-я строка не содержит больше отрицательных элементов в столбцах векторов .

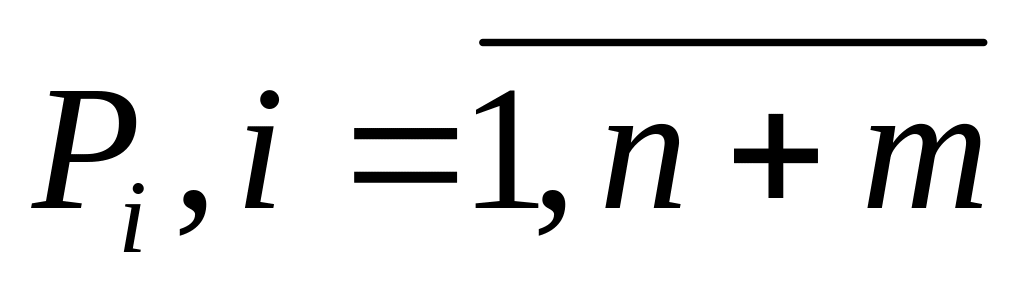В первом случае базис отвечает некоторому опорному плану исходной задачи и определение ее оптимального плана продолжают по (m+1)-ой строке.

Во втором случае, если элемент, стоящий в (m+2)-ой строке столбца вектора P₀ отрицателен, то исходная задача не имеет решения; если же он равен 0, то найденный опорный план исходной задачи является вырожденным и базис содержит, по крайней мере, один из векторов искусственного базиса. Если исходная задача содержит несколько единичных векторов, то их следует включить в искусственный базис.

Пример 1. Найти min функции при условиях:

Решение.

Канонический вид:

_.

Запишем систему ограничений в векторной форме: где

Среди векторов , только 2 единичных (P₄ и P₅). Поэтому к левой части 3-го уравнения системы ограничений ЗЛП в каноническом виде прибавим дополнительную переменную (искусственную) и рассмотрим расширенную ЗЛП:

Расширенная задача имеет опорный план X=(0;0;0;24;22;0;10), определяемый системой трех единичных векторов P₄, P₅, P₇, где . Вектор-столбец будет иметь вид: .

Вначале вычислим значения ;

(для векторов базиса).

Рассчитанные величины поместим в 4-ой и 5-ой строках первой симплекс-таблицы, в 4-ой строке – слагаемые, не содержащие М, в 5-ой строке – содержащие М. Так как в 5-ой строке в столбцах векторов , имеются отрицательные числа, то данный опорный план не является оптимальным.

Наибольшее по модулю отрицательное число в 5-ой строке (-2) определяет вектор P_3, который нужно ввести в базис. Для определения вектора, выводимого из базиса, вычисляем т.е. число 2 будет разрешающим элементом. Строка, в которой он находится, указывает на вектор P₇, который нужно вывести из базиса. Так как этот вектор искусственный, поэтому в дальнейшем столбец данного вектора не заполняется.

Все дальнейшие вычисления проводим по обычным правилам симплекс-метода и оформляем в виде последовательности симплекс-таблиц.

i	Базис		P0	2	-3	6	1	0	0	-M
				P1	P2	P3	P4	P5	P6	P7
1	P4	1	24	2	1	-2	1	0	0	0
2	P5	0	22	1	2	4	0	1	0	0
3	P7	-M	10	1	-1	2	0	0	-1	1
4			24	0	4	-8	0	0	0	0
5			-10	-1	1	-2	0	0	1	0
1	P4	1	34	3	0	0	1	0	-1
2	P5	0	2	-1	4	0	0	1	2
3	P3	6	5	1/2	-1/2	1	0	0	-1/2
4			64	4	0	0	0	0	-4
1	P4	1	35	5/2	2	0	1	1/2	0
2	P6	0	1	-1/2	2	0	0	1/2	1
3	P3	6	11/2	1/4	1/2	1	0	1/4	0
4			68	2	8	0	0	2	0

Оптимальный план:

.

Пример 2. Найти min функции

при условиях

Канонический вид:

Запишем систему ограничений в векторной форме: где

Т.к. среди векторов имеется только один единичный (Р₃), то находим решение расширенной задачи, состоящей в определении максимального значения функции

при условиях

Расширенная задача имеет опорный план , определяется системой трёх единичных векторов Р₃, Р₇ и Р₈.

i	Базис			-2	1	0	1	0	0	-M	-M
				P1	P2	P3	P4	P5	P6	P7	P8
1	P3	0	10	1	-2	1	0	0	0	0	0
2	P7	-M	18	-2	-1	0	-2	-1	0	1	0
3	P8	-M	36	3	2	0	1	0	-1	0	1
4			0	2	-1	0	-1	0	0	0	0
5			-54	-1	-1	0	1	1	1	0	0
1	P3	0	46	4	0	1	1	0	-1	0
2	P7	-M	36	-1/2	0	0	-3/2	-1	-1/2	1
3	P2	1	18	3/2	1	0	1/2	0	-1/2	0
4			18	7/2	0	0	-1/2	0	-1/2	0
5			-36	1/2	0	0	3/2	1	1/2	0

Т.к. , а , то в базис на первой итерации вводим вектор Р₂. , т.е. из базиса выводим вектор Р₈.

В пятой строке второй симплекс-таблицы в столбцах векторов , не содержится отрицательных элементов. В столбце же вектора Р₀ этой строки имеется отрицательное число (-36). Следовательно, исходная задача не имеет оптимального плана.