Учебное пособие 2214

Воронежский государственный технический университет

Voronezh State Technical University

канд. физ.-мат. наук, профессор А.Д. Кононов,

Ph. Phy.-Mat. in Engineering, Prof. A.D. Kononov,

д-р техн. наук, профессор А.А. Кононов,

D. Sc. in Engineering, Prof. A.A. Kononov,

канд. техн. наук, доцент С.А. Иванов

Ph. D. in Engineering, assistant professor S.A. Ivanov

Россия, г. Воронеж,

E-mail: kniga126@mail.ru

Russia, Voronezh, E-mail: kniga126@mail.ru

Для

исследования 2

свойств информа-

ческой радиосвязи, использующих простран-

ционного

радиоканала

необходимо иметь

ственно - временные характеристики элек-

данные о характеристиках среды распро-

тромагнитных колебаний для сбора и

странения электромагнитных волн, структу-

обмена информацией в системах организа-

ре передаваемых по каналу сигналов, в част-

ционного управления со значительным тер-

ности их поляризации [1-3]. При решении

риториальным

разнесением

управляемых

проблемы

оптимизации

информационного

объектов [7, 8].

обеспечения автоматизированного управле-

При решении практических задач по-

ния крупными разветвленными технологиче-

вышения помехоустойчивости

информаци-

скими структурами особенно высокие требо-

онных систем связи и управления для оценки

вания с учетом значительного разнесения

достоинств различных способов передачи

управляемых объектов предъявляются к си-

сообщений обычно применяется коэффици-

стемам обмена информацией. На основе

ент β – эффективности [8-11] – так называе-

сравнительного анализа [4-6] были опреде-

мый выигрыш системы

лены потенциальные возможности различ-

QВЫХ

ных способов передачи информации на

В

,

(1)

большие расстояния и рассмотрены некото-

QВХ

рые специальные вопросы оптимизации ин-

где QВХ – отношение средних мощностей

формационного обеспечения перспективных

сигнала и помехи на входе приемника; QВЫХ

систем управления (СУ), определившие

– отношение средних мощностей сигнала и

необходимость применения средств косми-

помехи на выходе приемника.

Для изотропных сред распространения

© Кононов А.Д., Кононов А.А., Иванов С.А., 2019

ВЫПУСК № 2 (16), 2019

ISSN 2618-7167

характеристика В исследована с достаточной

менный слой эллиптически поляризованной

полнотой [9]. Будем рассматривать эллипти-

волны как вхождение в гиромагнитную сре-

чески поляризованный сигнал, прошедший

ду двух ортогонально поляризованных коле-

анизотропный канал распространения, прием

баний с различными фазовыми сдвигами

которого осуществляется двумя ортогональ-

между ними [10]. При излучении волны го-

ными антеннами, согласованными с поляри-

ризонтальной поляризации θ = 0 и выраже-

зационным базисом излучаемой волны. По-

ние (2) принимает вид

ляризационная структура эллиптически по-

cos

ляризованной волны характеризуется коэф-

(3)

E

.

фициентом эллиптичности К, углом про-

j sin

странственной ориентации эллипса поляри-

Пусть излучается волна линейной по-

зации θ и направлением вращения вектора

Е0е

j( 0t 0 )

напряженности

электрического поля.

Как

ляризации

EИ

(Е0 – амплиту-

известно,

коэффициентом

эллиптичности

да сигнала, ω0

и ψ0 – частота и фаза), несу-

называется

отношение

амплитуд

векторов

щая

полезное

сообщение.

В

анизотропном

напряженности

электрического поля глав-

канале

распространения

она претерпевает

ных полуосей

(малой к

большой) эллипса

трансформацию поляризационной структуры

ЕМИН

К

и становится

эллиптически поляризованной.

Е

МАХ

Деполяризация волны в этом случае может

поляризации

В практике такое

быть описана следующим преобразованием

выражение коэффициента эллиптичности не

всегда является удобным, то есть обычно по-

cos

луоси эллипса ЕМИН, ЕМАХ связывают с си-

EР

ЕИ

,

(4)

стемой координат XOY, поэтому в процессе

j sin

изменения формы эллипса, роль проекций

EX, EY

по отношению наименования полу-

где EР - комплексный вектор распространя-

осей эллипса может меняться. Поэтому вме-

ющегося колебания.

сто коэффициента К удобно пользоваться

Пусть теперь передаваемое сообщение

понятием угла эллиптичности φ, который

в условиях квазипродольного распростране-

представляет собой половинный угол между

ния проходит через гиротропную среду, ха-

большими

диагоналями прямоугольника,

рактеризующуюся комплексной поляризаци-

описанного около эллипса поляризации,

онной матрицей пропускания [8, 11]

главные оси которого совмещены с осями

1

e j 1

e j 2

j(e j 2

e j 1 )

симметрии

прямоугольника

[10].

Угол

эл-

П

e j 2 )

e j 1 e j 2

,

(5)

липтичности представляется через коэффи-

2

j(e j 1

циент

эллиптичности

выражением

где φ1, φ2

– соответственно набеги фаз не-

arctgK

и может изменяться в пределах

обыкновенной и обыкновенной нормальных

волн при распространении в магнитоактив-

4

4

ной среде. Считая затухания ортогональных

В работах [10, 11] показано, что дву-

компонент

соизмеримыми [12,13], прохож-

мерный сигнал с нормированной амплитудой

дение

сигнала

представляется матричным

в ортогонально эллиптическом базисе опи-

уравнением

сывается матрицей

(6)

cos cos j sin sin

EР

П

ЕИ .

(2)

На выходе

приемных

ортогональных

E

.

cos sin j sin cos

антенн формируются выходные эффекты

E

0

(e j 1

e j 2

)cos (e j 2 e j 1 )sin e j( 0 0 )

е (t) Re

n(t),

1

2

E

0

j(e j 1

e j 2

)cos j(e j 1 e j 2 )sin e j( 0

0 )

е2

(t) Re

n(t),

(7)

2

D

cos2 m

sin2 m

D

cos2 m

sin2 m

D

01, 2

(13)

cos2 m cos2 m (D2 D2 ) sin2 m sin2 m D D .

В качестве

иллюстрации рассмотрим

но линейном базисе. В этом случае

излучение произвольно

ориентированной

начальные

значения ξ = 0, mξ = 1, Dξ =

линейно поляризованной волны, а прием ее

0 и результаты расчета представлены на

на две антенны в произвольном ортогональ-

рис. 1 и 2.

ВЫПУСК № 2 (16), 2019

ISSN 2618-7167

Графики на рис. 1 и 2 показывают за-

сеанса связи. На этих рисунках штриховая

висимости среднего значения m01, 2

и дис-

линия соответствует значению

mΦ = 0,5;

персии D

выигрыша

по обеим

ортого-

сплошная – значению mΦ = 1.

На рис. 1

нижние две кривые, не превышающие значе-

01, 2

нальным

компонентам

приемной

антенны

ния m01, 2 1 , соответствуют приему по ор-

для ряда значений mΦ и DΦ, определяемых

тогональному, а верхние – по совпадающему

случайным характером состояния ионосфер-

каналу.

ного канала передачи информации во время

При распространении электромагнит-

стабильности состояния параметров ионо-

ной волны в реальных магнитоактивных

сферного канала наряду с ухудшением каче-

средах угол поворота плоскости поляриза-

ства получения информации по одной из ор-

ции является случайной величиной, обу-

тогональных компонент наблюдается улуч-

словленной

наличием неоднородностей и

шение надежности приема по другой орто-

флуктуаций в ионосфере электронной кон-

гонально поляризованной составляющей по-

центрации, магнитного поля Земли, геомет-

ля приемной антенны. Рис. 2 показывает, что

рии слоев и траектории распространения

разброс значений параметров ионосферного

сигнала. Из

рис. 1 следует, что с ростом не-

канала не слишком существенно отражается

на стабильности и качестве передачи инфор-

учебных заведений. Строительство. – 2011. –

мации через гиротропную среду, что также

№ 10(634). – С. 74 – 79.

подтверждает целесообразность применения

7. Кононов А.Д. Разработка алгоритма

двумерных сигналов и методов поляризаци-

определения координат и сигнала рассогла-

онной селекции с целью повышения помехо-

сования в задаче автоматического управле-

устойчивости в системах связи и управления,

ния мобильными объектами в дорожном

использующих ионосферный радиоканал.

строительстве / А.Д. Кононов, А.А. Кононов

Библиографический список

// Вестник Воронежского государственного

университета. Серия: Системный анализ и

1. Кононов А.Д. Алгоритм формирова-

информационные технологии. – Воронеж. –

ния сигналов управления в системах следя-

2014. – № 1. – С. 84 – 89.

щего дистанционного управления землерой-

8. Кононов А.Д. К вопросу оптимиза-

но-транспортными машинами / А.Д. Коно-

ции информационных систем передачи ко-

нов, Ю.В. Авдеев, А.А. Кононов // Известия

манд управления через анизотропные среды /

высших учебных заведений. Строительство.

А.Д. Кононов, А.А. Кононов, С.А. Иванов //

– 2010. – № 1(613). – С. 81 – 86.

Информационные технологии в строитель-

2. Авдеев Ю.В. К вопросу исследова-

ных, социальных и экономических системах

ния радиоволнового канала системы дистан-

– 2018. – №.1-2 (11-12). – С. 29 – 34.

ционного

управления

землеройно-

9. Смирнов В.А. Приближенные мето-

транспортными машинами / Ю.В. Авдеев,

ды расчета искажений в системах передачи

А.Д. Кононов, А.А. Кононов, В.Н. Аникин //

информации / В.А. Смирнов // – М.: Связь. –

Известия высших учебных заведений. Стро-

1975. – 432 с.

ительство.– 2010. – № 10(622). – С. 86 – 92.

10.

Поздняк С.И. Введение в статисти-

3. Кононов А.Д. К вопросу о влиянии

ческую

теорию поляризации радиоволн /

рассогласования по поляризации информа-

С.И. Поздняк, В.А. Мелитицкий // – М.: Со-

ционного сигнала и характеристик антенн в

ветское радио. – 1974. – 480 с.

магнитоактивном канале распространения на

11. Гильмутдинов В.И. Система эф-

эффективность систем связи и управления /

фективного интерфейса исходных данных с

А.Д. Кононов, А.А. Кононов, А.Е. Готовцева

вычислительным устройством / В.И. Гиль-

// Информационные технологии в строитель-

мутдинов, А.А. Кононов // Информационные

ных, социальных и экономических системах

технологии в строительных, социальных и

– 2018. – № 1-2 (11-12). – С. 66 – 69.

эконом. системах–2018 –№3(13). –С. 6–10.

4. Маршаков В.К. Анализ систем тра-

12.

Авдеев Ю.В. Разработка алгоритма

екторного сопровождения мобильных объек-

определения координат в задаче дистанци-

тов с автоматическим управлением / В.К.

онного управления движением машинно-

Маршаков, А.Д. Кононов, А.А. Кононов // В

тракторных агрегатов / Ю.В. Авдеев, А.Д.

сборнике: Радиолокация, навигация, связь.

Кононов, А.А. Кононов // В сборнике: Меха-

XXI Международная научно-техническая

низация и электрификация сельского хозяй-

конференция.–Воронеж.–2015.–С.1296–1304.

ства. – Минск. – 2012. – № 46. – С. 24–31.

5. Авдеев Ю.В. Сравнительный анализ

13.

Кононов А.Д. Обработка информа-

фазовых методов определения координат в

ции радионавигационной системы для согла-

задачах дистанционного

автоматического

сования

с исполнительными механизмами

управления

машинами

дорожно-

мобильного объекта / А.Д. Кононов, А.А.

строительного комплекса

/ Ю.В.

Авдеев,

Кононов, А.Ю. Изотов // В сборнике: Ин-

А.Д. Кононов, А.А. Кононов, Н.А. Варданян

форматика: проблемы, методология, техно-

// Известия высших учебных заведений.

логии. Материалы ХV международной науч-

Строительство. – 2014. – № 1(661).–С.86–93.

но-методической конференции. – Воронеж. –

6. Авдеев Ю.В. Устройство цифровой

2015. – С. 99–102.

обработки выходных сигналов координато-

14. Мардиа К. Статистический анализ

мерной системы для дистанционного управ-

угловых наблюдений / К. Мардиа // – М.:

ления землеройно-транспортными машина-

Наука. – 1978. – 270 с.

ми / Ю.В. Авдеев, А.Д. Кононов, А.А. Коно-

нов, Н.А.

Варданян // Известия

высших

Воронежский государственный технический университет

Voronezh State Technical University

канд. физ.-мат. наук, доцент Л.В. Стенюхин

Ph. D. in Phys. –Math. Sciences, associate professor L.V. Stenyukhin

Россия, г. Воронеж, E-mail: stenyuhin@mail.ru

Russia, Voronezh, E-mail: stenyuhin@mail.ru

x

1

поверхность Шерка u(x, y) = y,

,

ln(2 x

2

y)

, = { < x <

,

< y <

};

cos

cos y

2

2

2

2

1

3

1

3

2

2

2

2

поверхность Эннепера u(x, y) =

xy

x

x,

y

x

y y, y

x

,

= R

.

3

3

ВЫПУСК № 2 (16), 2019

ISSN 2618-7167

Поэтому

задача

сводится

к

Дирихле на множестве

исследованию

на экстремум

функционала

(5)

Для удобства положим F(u) = F1 (u) F2 (u),

Утверждение.

Функционал Дирихле

F:W 2

( ) W1( ) W1( )

D(u)

и отображение

f (u) выпуклые.

4

2

2

Для

доказательства

достаточно

и множество (5) представится

проверить для них неравенство Иенссена, то

(6)

есть выполнение неравенств

u u

2

D(u ) D(u

2

)

u u

2

f (u ) f (u

2

)

D

1

1

, f

1

1

.

2

2

2

2

Это

обстоятельство

позволяет

далее

частности, её субдифференциальную форму.

применить

теорему

Куна-Таккера [7],

в

Образуем функцию Лагранжа

(7)

(8)

По

теореме Куна-Таккера,

если

(10)

функция u из множества (6) является

условным

экстремумом

функционала

Функционал

Дирихле

является

Дирихле, то имеет место включение

гладким,

поэтому

D(u) = u,

–

(9)

лапласиан.

Отображение

F гладкое

на

W 2

( ), следовательно

оператор

F (u)

где – субдифференциал отображений

D, F

4

имеет вид

и f . Рассмотрим его сечение

(11)

Найдём f (u). Для любого возмущения h W 2

( )

имеем

4

В качестве u* можно взять малую

Граничный

контур

фиксируется

2

условием

по норме W4 ( ) функцию. Таким образом,

уравнение (9) имеет вид

(13)

(12)

После преобразований,

аналогичных

где F'* (u) – сопряжение отображения F' (u),

[5], задача (12) – (13) записывается

системой

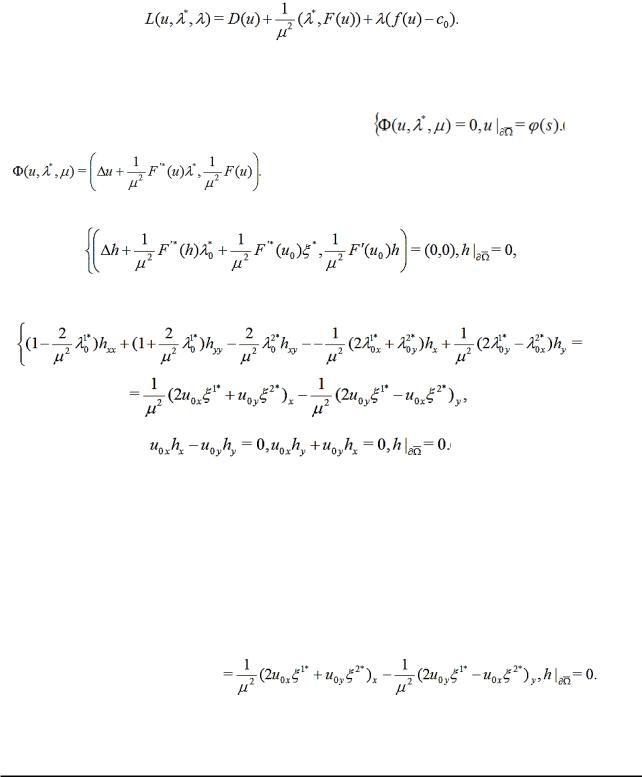
ВЫПУСК № 2 (16), 2019

ISSN 2618-7167

'

'

~

~

f (u) = u(x0 , y0 ) = u( x0 , y0 ) = u (x0

, y0 ) = f (u),

*

* '

'

=

2

~*

2

~*

f (u h) f (u) (u

, h) = u hdx dy

u

hdxdy = (

u

, h).

Образуем функцию Лагранжа

L (u, * , ) = D (u) ( * , F (u)) ( f

(u) c ).

0

С учётом вышеизложенного, на области функция Лагранжа имеет вид

(17)

Дифференцируя функцию Лагранжа по

Исследуем на

существование

точек

u и по * , получим оператор

Плато-

бифуркации задачу

Лагранжа в координатах (x, y)

,

который

(19)

выглядит следующим образом

(18)

Линеаризованная по (u, * ) в

точке

(u

, * )

задача имеет вид

0

0

(20)

(21)

Чтобы применить теорему Крэндалла-

системы уравнений (21). В начале исследуем

Рабиновича из [9] надо вычилить ядро

на разрешимость относительно h задачу,

линеаризованного оператора, порожденного

определяемую

первым

и

последним

задачей (20). Для этого необходимо и

уравнениями системы (21), то есть задачу

достаточно

установить

разрешимость

{(1

2

1* )h

(1

2

1* )h

2

2*h

1

(21*

2* )h

1

(21*

2* )h

=

y

2

0 xx

2

0 yy

2

0 xy

2

0 x

0 y x

2

0 y

0 x

(22)