Учебное пособие 1714

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Воронежский государственный архитектурно–строительный университет

С.М. Алейников, В.В. Горяйнов

ОСНОВЫ ТЕОРИИ ГРАФОВ

Учебное пособие

Рекомендовано в качестве учебного пособия редакционно-издательским советом Воронежского государственного архитектурно–строительного университета для студентов, обучающихся по специальности 270115

«Экспертиза и управление недвижимостью»

Воронеж 2009

Введение

Предлагаемое учебное пособие содержит теоретический материал и варианты расчетно-графической работы по курсу «Теория графов», изучаемому студентами специальности 270115 «Экспертиза и управление недвижимостью» Воронежского государственного архитектурно-строительного университета.

Пособие возникло на основе курса лекций, читаемых профессором С.М. Алейниковым студентам строительного факультета Воронежского государственного архитектурно-строительного университета. Задания расчетнографической работы составлены совместно профессором С.М. Алейниковым и доцентом В.В. Горяйновым.

Данное пособие состоит из пятнадцати глав и двух приложений. Первая глава включает основные определения, понятия и термины теории графов.

Во второй главе вводится понятие геометрических графов, а в третьей рассказывается, как определить степени вершин у неорграфа и полустепени исхода и захода вершин у орграфа.

Изоморфизму графов посвящена четвертая глава.

Впятой рассматривается построение матриц смежности и инцидентности для неорграфов и орграфов.

Вшестой главе описаны такие операции над графами, как их пересечение, объединение, симметрическая разность, удаление ребер и вершин. Также в шестой главе рассмотрены части графов.

Полные, взвешенные, двудольные, однородные, плоские и планарные графы описаны в седьмой главе.

Понятие маршрута в графе дано в восьмой главе. Там же рассматриваются такие разновидности маршрутов, как цепь и путь, составная цепь и составной путь, простая цепь и простой путь, цикл и контур, простой цикл и простой контур. Здесь же показано, как выявить в графе маршрут заданной длины и найти кратчайший путь в орграфе.

Девятая глава посвящена связности ориентированных и неориентированных графов. Описано построение матриц достижимости и контрдостижимости, а также рассмотрен вопрос о вершинной и реберной связности графов.

Вдесятой главе показано, как вычислить эксцентриситет вершин графа, радиус, диаметр и центр графа.

Эйлеровы и гамильтоновы графы рассмотрены в одиннадцатой главе, а двенадцатая посвящена деревьям. В ней содержатся сведения о свойствах деревьев, о типах вершин и центрах дерева. Также описаны корневые и покрывающие деревья.

Втринадцатой главе приведены такие экстремальные задачи на графах, как задача об остове наименьшего веса и задача о коммивояжере. Рассмотрены различные алгоритмы их решения.

Четырнадцатая глава посвящена задачам сетевого планирования. В ней

5

рассмотрен принцип построения сетевого графика, приведен алгоритм получения правильной нумерации вершин сети и формулы, позволяющие рассчитать ранние и поздние сроки свершения событий, резервы времени событий, ранние и поздние сроки начала и окончания всех работ, а также полные и свободные резервы времени работ.

Варианты и характеристика заданий расчетно-графической работы приведены в пятнадцатой главе. Расчетно-графическая работа состоит из шести заданий, включающих понятия неориентированного, ориентированного и взвешенного графов, понятие операций над графами и построения кратчайшего пути в орграфе и сетевого графика.

Подробное решение всех задач, входящих в расчетно-графическую работу, приведено в тексте учебного пособия.

В приложениях приведены основные операторы пакета networks программы Maple для работы с графами и биографические сведения об ученых, работавших в области теории графов.

Авторы выражают благодарность кандидату физ.-мат. наук, доценту А.М. Дементьевой, внимательно прочитавшей рукопись. Ее ценные замечания и рекомендации помогли улучшить содержание пособия

6

1. Основные определения теории графов

Теория графов как наука

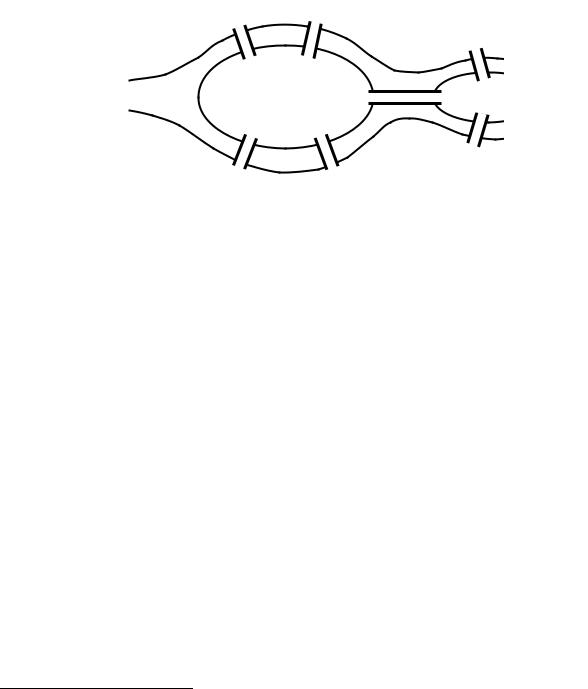
Начало теории графов относят к 1736 году, когда Леонард Эйлер* решил популярную в то время задачу о кенигсбергских мостах (рис. 1): можно ли пройти по всем семи мостам города Кенигсберга через реку Преголь по одному разу и вернуться к исходной точке.

C

B

Рис. 1. Задача о кенигсбергских мостах

Эйлером было доказано, что это невозможно. Однако этот результат в течение ста лет оставался единственным результатом теории графов. Толчок к развитию теория графов получила в середине XIX века, когда Густав Роберт Кирхгоф* применил графы для анализа электрических цепей, а Артур Кэли* использовал графы при изучении молекул углеводорода.

Внастоящее время теория графов используется при решении практических задач, в которых необходимо изучить не только совокупность объектов, но и условия связей между ними. К таким задачам относятся:

●транспортные схемы, линии метро;

●электрические цепи;

●структура атомов в органических молекулах;

●экономические связи между странами;

●инженерные сети (водопровод, вентиляция);

●склады и торговые предприятия;

●календарно-сетевое планирование и управление;

●многозвенные механизмы;

●генеалогические деревья.

Вэтих и подобных случаях удобно изображать рассматриваемые объекты точками, называемыми вершинами, а связи между ними линиями, называемы-

*Биографические сведения см. в прил. 2.

7

ми рёбрами.

Совокупность вершин V , связи между которыми определены множеством рёбер U , называется графом и обозначается G =<V , U >.

Примерами объектов, которые удобно представлять вершинами графа для решения практических задач, служат аэропорты, рубильники, трансформаторы и т.д., а связи между такими вершинами удобно характеризовать посредством рёбер, которым соответствуют авиалинии, линии электропроводки и т.д.

Например, предположим, что пять государств A, B, C, D и E для договорённости о сотрудничестве послали своих представителей на конференцию. Результатом переговоров стало подписание шести договоров: A и C, B и C, A и D, D и B, E и A, B и E. Данной ситуации соответствует граф, имеющий пять вершин и шесть рёбер. Геометрическое изображение этого графа может иметь один из видов, представленных на рис. 2.

A C E B

D

A B C D E

Рис. 2. Виды геометрического изображения графа

Основные определения, понятия и термины теории графов

Граф G считается заданным, если заданы два множества: непустое множество V ={υ1,υ2,…,υn} вершин графа и множество U ={u1,u2,…,um} рёбер графа, и обозначается G =<V , U >.

Множество V называется носителем графа, а множество U – его сигна-

турой.

Число n = V вершин графа G называется его порядком. Если число рёбер графа G равно m = U , то G называют (n,m) графом.

Если m и n меньше бесконечности, то граф G называется конечным, в противном случае – бесконечным.

Каждое ребро графа представляет собой упорядоченную или неупорядоченную пару элементов множества V.

Упорядоченная пара вершин υi и υj графа обозначается υi ×υj . Не-

8

упорядоченная пара обозначается υi &υj . Очевидно, что когда υi ≠υj , то

υi ×υj ≠υj ×υi , в то же время υi &υj =υj &υi .

Если ребра графа представляют упорядоченные пары вершин, то он называется орграфом (ориентированным графом), а если неупорядоченные, то неорграфом (неориентированным графом).

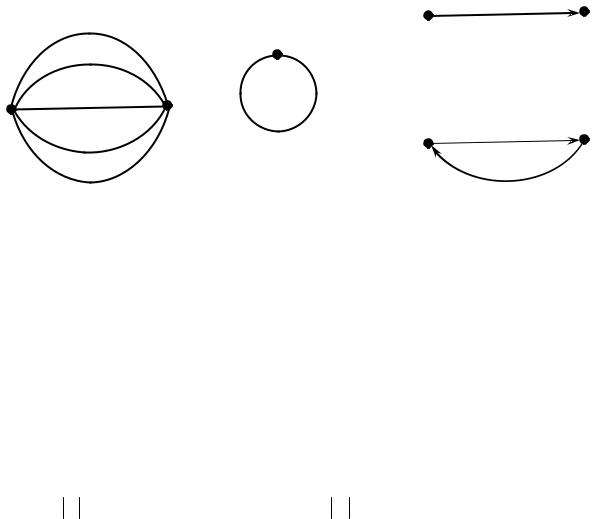
Различные рёбра графа могут соответствовать одним и тем же парам его вершин. Такие рёбра называются кратными, или параллельными (рис. 3).

Рёбра графа, отвечающие парам одинаковых вершин, называются петлями (рис. 4). Для них υi &υi =υi ×υi .

Рёбра графа, соединяющие упорядоченную пару различных вершин, на-

зываются дугами, или ориентированными рёбрами (рис.5). Как видно из рис. 5, ориентация ребра указывается стрелкой и при этом говорят, что ребро u1

исходит из вершины υ1 и заходит в вершину υ2 . В этом случае вершина υ1 на-

зывается начальной вершиной ребра u1 , а υ2 – конечной вершиной. Пары дуг υi ×υj и υj ×υi называются противоположно направленными (рис. 6).

Рёбра, соединяющие неупорядоченные пары вершин, называются звень-

ями, или неориентированными рёбрами. Например, у графа на рис. 2 все ребра являются звеньями.

В связи с введением понятий о дуге и звене в графе можно дать еще одно определение ориентированного и неориентированного графов:

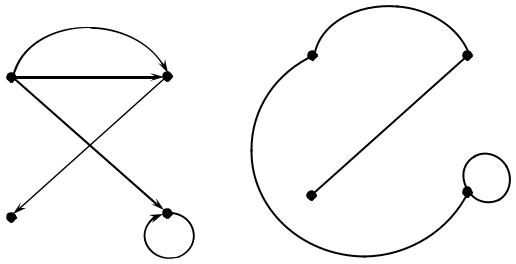
орграф – это граф, рёбрами которого являются либо дуги, либо петли

(рис. 7);

неорграфом называется граф, рёбрами которого могут быть только звенья или петли (рис. 8).

На рис.7 и 8 изображены графы четвертого порядка или (4,5) - графы,

так как n = V = 4 (V ={υ1,υ2,υ3,υ4}), а m = U =5 (U ={u1, u2, u3, u4, u5}).

9