Учебное пособие 1714

7. Типы конечных графов

7.1. Полный граф

Простой граф, в котором любые две вершины соединены ребром (являются смежными), называется полным.

Полный граф с n вершинами обозначается Kn (рис. 29).

а)

Рис. 29. Полные графы: а) K1, б) K2 , в) K3 , г) K4 , д) K5

31

Такое название графа связано с тем, что турниром называют состязание, правила которого предписывают его участникам встречаться друг с другом только один раз и запрещают ничейный исход.

В графе-турнире вершинами считаются все участники состязания, и для каждой пары дуга идёт от победителя к побеждённому участнику.

в)

Рис. 30. Турнир: а) с двумя вершинами; б) с тремя вершинами; в) с четырьмя вершинами

7.2. Взвешенный граф

Для более детального описания связей между объектами рёбрам графа приписываются количественные значения или характерные свойства объекта, которые называются весами. Это могут быть порядковые номера, приоритетные при рассмотрении рёбер. Вес может означать длину пути, пропускную способность, напряжение или силу тока в электрической цепи, валентные связи в химической формуле, количество рядов в движении на автодороге, характер отношений между людьми.

Вес можно приписывать также и вершинам. Вершины, соответствующие

32

населённым пунктам, могут характеризоваться числом мест в гостинице и т.п. Другими словами, вес вершины может означать любую характеристику соответствующего объекта (атомный вес элемента, вес человека и т.д.).

Графы, рёбрам и (или) вершинам которых приписаны некоторые веса, называются взвешенными графами (рис. 31).

υ1

υ3

Рис. 31. Взвешенный орграф

Графы, вершины которых пронумерованы, называются помеченными,

или перенумерованными графами (рис. 32).

Взвешенный помеченный орграф без петель, у которого выделены две вершины (исток и сток), называется сетью (рис. 33).

Информацию о весах ребер во взвешенном графе можно представить в виде матрицы весов W =(wij ), где элементам wij приписываются следующие значения:

33

● если звено (дуга), соединяющее(ая) вершину υi с υj , существует, то wij равен весу этого ребра;

●если звено (дуга), соединяющее(ая) вершину υi с υj , не существует, то wij помечают знаком ∞;

●если петель нет, то элементы wii = 0 .

Из вышесказанного следует, что матрица весов является квадратной матрицей размера n ×n .

Пример 7.1. Составить матрицу весов для взвешенного орграфа, представленного на рис. 31.

Решение. Матрица весов для данного орграфа будет являться матрицей пятого порядка. Так как петель нет, то все элементы wii = 0 . Элемент w12 = 2,

так как существует дуга, соединяющая вершину υ1 с вершиной υ2 и ее вес равен двум. Элементы w13 = w14 = w15 = ∞, потому что вершина υ1 не соединена с вершинами υ3 , υ4 и υ5 (не существует дуг, выходящих из υ1 и заходящих в υ3 , υ4 и υ5 ). Аналогично находим все остальные элементы матрицы весов и в итоге получаем

7.3. Однородные графы

Граф называется однородным (регулярным) степени K, если степени всех его вершин равны и равны K.

Математически это условие записывается следующим образом:

Однородный граф первой степени называется паросочетанием (рис. 34). На рис. 29, в представлен однородный граф второй степени (полный

граф K3 ). Примерами однородных графов могут служить графы, образованные

ребрами правильных многогранников. К ним относят тетраэдр, гексаэдр (куб), додекаэдр ( K =3 ); октаэдр ( K = 4 ); икосаэдр ( K =5 ). Тетраэдр имеет 4

34

Рис. 34. Паросочетание ( K =1)

треугольные грани, 6 рёбер и 4 вершины. Куб имеет 6 квадратных граней, 12 рёбер и 8 вершин. Додекаэдр имеет 12 пятиугольных граней, 30 рёбер и 20 вершин. Октаэдр имеет 8 треугольных граней, 12 рёбер и 6 вершин. Икосаэдр имеет 20 треугольных граней, 30 рёбер и 12 вершин.

Однородные графы третьей степени называются кубическими, у них всегда чётное количество вершин. Известным примером кубического графа является граф Петерсена (рис. 35).

υ6

υ5

Рис. 35. Граф Петерсена*

Для однородных графов формула (3.2) принимает вид

* Биографические сведения см. в прил. 2.

35

Из формулы (7.3) видно, что если K нечётное, то n должно быть чётное. У

любого однородного графа нечётной степени всегда будет чётное количество вершин.

7.4. Двудольный граф

Если множество вершин графа можно разбить на два непересекающихся подмножества (две доли V1 и V2 ), т.е.

V=V1 V2, V1 ∩V2 = ,

ине существует рёбер, соединяющих вершины одного и того же подмножества, то граф называется двудольным.

Двудольный граф называется полным, если каждая вершина одной доли соединена с каждой вершиной другой доли. Полный двудольный граф обозначается следующим образом:

Kn1, n2 ,

где n1 = V1 и n2 = V2 .

На рис. 36 приведены классические примеры двудольных графов.

Рис. 36. Двудольные графы: а) K3,3 , б) K1,4

Штриховой линией на рис. 36 обведены вершины, образующие непересекающиеся подмножества V1 и V2 .

36

7.5. Плоские и планарные графы

Ранее уже отмечалось, что возможно несколько изображений одного графа, поскольку все изоморфные графы несут одну и ту же информацию. На практике при изготовлении микросхем необходимо выяснить, можно ли схему радиоэлектронного устройства, которая представляет собой граф, изобразить на плоскости без пересечений проводников. Аналогичная задача возникает и при проектировании железнодорожных и других путей, где нежелательны переезды. Таким образом, возникает задача построения и исследования плоского графа.

Геометрический граф называется плоским, если он нарисован на плоскости так, что все его рёбра пересекаются только в вершинах. Любая точка пересечения его ребер будет вершиной графа, инцидентной рёбрам, пересекающимся в этой вершине (рис. 37).

Любой граф, изоморфный плоскому графу, называется планарным.

О планарных графах говорят, что они «укладываются» на плоскости. Планарный граф можно «положить» на плоскость, а плоский граф уже уложен на плоскости и является одним из изображений планарного графа. Не каждое изображение планарного графа является плоским графом.

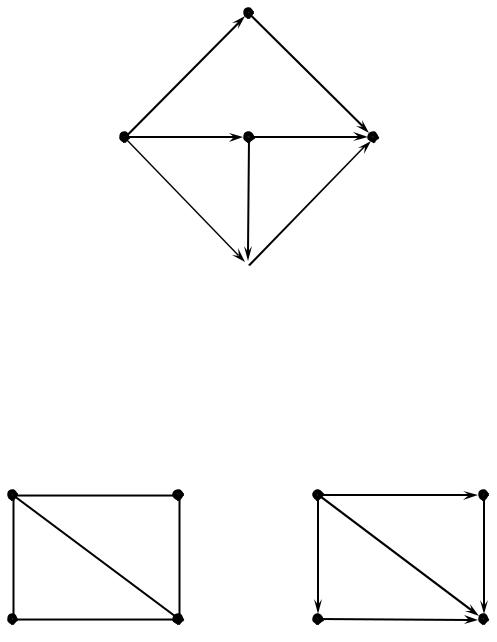
На рис. 38 изображен планарный граф, а на рис. 39 – его «плоская укладка», т.е. изоморфный ему плоский граф.

Рис. 37. Плоский граф Рис. 38. Планарный граф Рис. 39. Плоский граф

Существуют графы, не являющиеся планарными. Классическим примером не планарных графов являются графы Понтрягина*-Куратовского* K5 и

K3,3 (рис. 40). Отметим, что граф K3,3 возник в известной задаче «о трех домах

и трех колодцах», в которой жители домов хотели бы ходить за водой к любому колодцу так, чтобы их тропы не пересекались, т.е. чтобы никогда не встречать своих соседей. Для этого граф, соединяющий дома и колодцы, должен быть планарным. Однако он непланарен, так что эта задача не имеет решения.

* Биографические сведения см. в прил. 2.

37

Прежде чем привести критерии планарности графов, выясним, какие графы являются гомеоморфными.

Два графа называются гомеоморфными, если они получены из одного и того же графа подразбиением его рёбер (рис. 41).

Рис. 40. Графы Понтрягина–Куратовского: а) K5 , б) K3,3

υ2 υ2

υ4

Рис. 41. Гомеоморфные графы

Теорема 7.1 (Критерий Понтрягина-Куратовского планарности гра-

фов). Граф является планарным тогда и только тогда, когда он не содержит частей, гомеоморфных графам Понтрягина-Куратовского.

Теорема 7.2. Подграф планарного графа является планарным графом.

Теорема 7.3. Плоский граф не должен иметь своей частью графы Понтря- гина-Куратовского.

38

На рис. 42 – 47 ребра пронумерованы в порядке движения от вершины υ1

к вершине υ5 .

Маршрут, содержащий все вершины графа, называется остовным. Маршрут называется нетривиальным, если есть хотя бы одно ребро. Нуль-маршрут не имеет рёбер. В этом случае граф состоит из одной

вершины.

Если попарно различны все рёбра замкнутого маршрута, то такой маршрут в неорграфе называется циклом (рис. 48), а в орграфе – контуром (рис. 49).