
Практикум по высшей математике. дифференциальные уравнения и ряды. Пантелеев И.Н
.pdf
Подставляя частное решение в уравнение (10), получим
|
|
3 |
2 |
|
du |
|
|
|
sin x u sin |
|
x, |
u3 |
sin xdx, |
|
|||
u |
|
|
||||||
1 |
cos x C |
, |
u |
|
1 |
. |
||
2u2 |
|
2cos x 2C |
||||||
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
Таким образом, полагая 2C1 C , имеем
y |
sin x |
|
|
. |
|
2cos x C |
||
б) Разделим на x2 y2 правую и левую часть уравнения
1 |
1 |
|
|
y x y |
|
. |
(11) |
x2 y2 |
Теперь видно, что это уравнение Бернулли. Для его решения воспользуемся методом Лагранжа.
Найдем сначала решение однородного уравнения dyy dxx , ln y ln x ln C , y Cx .
Считаем, что C (х) - зависит от х, |
т. е. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
C x |
. |
|
|
|
|
|
|
(12) |
||||||
Подставим у и |
|
у' |
|
|
|
|
|
x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
в исходное уравнение (11) |
|
|||||||||||||||||||||
1 |
|
|
|
C |
|
C |
|
|
|
|
x2 |
|
|
|
|
2 |
|
|
|
||||
x C |
|
|
|
|
|
|
|
|
|
|
, |
|
C |
|
dC xdx, |
|
|||||||
x2 |
x2 |
x2C2 |
|
|
|||||||||||||||||||
C3 |
|
x2 |
|
C1 , |
|
|
C x 3 3 x2 |
3C1 . |
|
||||||||||||||
3 |
|
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3C1 C , |
||||
Таким образом, |
|
из |
выражения |
(12), |
полагая |
||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 3 |
|
|
3 |
|
|
C |
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
у |
|
|
|
|
|
|
|
2x |
x3 |
|
|
|
|
а х - за |
|||||||
в) Принимаем |
|
за независимую переменную, |
|||||||||||||||||||||
функцию. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21

dx |
|
2 |
|
2 |
, x |
x |
|
2 y y2 |
2x dy |
x |
|
2 y y |
|
|
|
2x . |
|
|
|
2 |
Последнее уравнение есть Воспользовавшись заменой х = uv,
|
|
|
|
|
|
|
v |
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
u v u v |
2 |
||||||||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv |
|
v |
, |
|
ln |
|
v |
|
|
|
1 |
|||
|
|
|
||||||||||||
dy |
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
уравнение |
Бернулли. |
||||
x |
|
|
|
|
получим |
||
|
u v |
v u |
|||||
2 y y2 |
. |
|
|
|
(13) |
||
|
2uv |
|
|
|
|||
|
|
|
|
|
|
||
y, |
v e |
|
y |
|
|
||
2 . |
|
||||||
Подставляя частное решение в уравнение (13), будем иметь
du |
e |
|
y |
|
2 y y2 |
2udu 2 y y |
2 |
e |
y |
dy, |
u |
2 |
2 |
e |
y |
. |
|||||
|
|||||||||||||||||||||
dy |
2 |
2ue |
|
y , |
|
|
|
C y |
|
||||||||||||
|
|
|
|
2 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, |
x |
C y2ey e |
или |
x2 |
C y2ey e y , |
|
|
|
|||||||||||||
2 |
|
|
|
||||||||||||||||||
x2 y2 Cey .
1.5. Уравнения в полных дифференциалах. Интегрирующий множитель
1°. Если для дифференциального уравнения
P x, y dx Q x, y dy 0 |
(1) |
|||
справедливо равенство |
|
|
|
|
P |
|
Q |
, |
(2) |
y |
|
x |
|
|
то уравнение называется уравнением в полных дифференциалах
и может быть записано в виде du (х, y) = 0.
а) Общий интеграл находится по одной из формул
u x, y xx P x, y dx yy Q x0 , y dy C, |
|
0 |
0 |
или |
(3) |
u x, y xx P x, y0 dx yy Q x, y dy C, |
|
0 |
0 |
22
где x0 , y0 - координаты некоторой фиксированной точки, причем
P2 x0 , y0 Q2 x0 , y0 0 .
б) Поскольку полный дифференциал функции и равен сумме частных дифференциалов ux dx Pdx, uy dy Qdy , то
интегрируя их по отдельности, считая в первом случае у постоянной, а во втором х, найдем два выражения для функции
u Pdx y ; u Qdy x , (4)
здесь y и x - некоторые функции.
Общее решение находится подстановкой в первое выражение вместо y всех членов из второго выражения,
зависящих только от у, или наоборот.
2°. Пусть левая часть уравнения (1) не является полным
дифференциалом, |
однако можно найти такую функцию |
|||||
x, y , что |
умножая уравнение на нее, произведение |
|||||
Pdx Qdy |
будет полным дифференциалом |
|
||||
|
|
P |
|
Q |
. |
(5) |
|
|
y |
|
|||
|
|
|
x |
|
||
Функция называется интегрирующим множителем и
легко находится в двух случаях:
а) если x , то из выражения (5) следует
|
P |
|
|
|
Q |
|
|
|
1 |
|
|
P |
Q |
|
|
||
|
Q |
|
или |
|
|
|
dx. |
(6) |
|||||||||
y |
x |
x |
|
Q |
y |
||||||||||||
|
|
|
|
|
|
x |
|
|
|||||||||
б) если |
y , то из выражения (5) следует |
|
|||||||||||||||
|
|
|
P |
|
Q |
|
|
|
1 |
|
Q P |
|
|
||||
P |
|
|
или |
|
|
dy. |
(7) |
||||||||||
y |
y |
x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
P |
x |
y |
|
|
||||||
23
Признаком существования интегрирующего множителя является отсутствие в выражении (6) переменной y, а в выражении (7) переменной х.
5.1. Решить уравнения: а) x y dx x 2 y dy 0 ;
|
x |
|
x |
x |
|
|
|
|
y |
y |
|
|
|||||
б) x e |
|
dx e |
|
|
|
1 |
|
dy 0 . |
|
|
|
||||||
|
|
|
|
y |
|
|
||
|
|
|
|
|
|
|
|
|
Решение. а) Вначале надо убедиться, что данное уравнение в полных дифференциалах. Полагая P = x + y; Q = x - 2у, подставляем их значения в выражение (2)
|
|
x y |
|
x 2 y |
1 . |
|
||||||||||||
|
|
y |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||
Так как равенство справедливо, то общий интеграл |
||||||||||||||||||
находим по формуле (3), считая, что x0 |
0, y0 |
0 |
||||||||||||||||
u 0x x y dx 0y |
2 ydy |
x2 |
xy y2 . |
|||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
Отсюда общее решение |
|
x2 |
|
xy y2 |
C . |
|
||||||||||||
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
|
x |
|
x |
|
|
|
|
||
|
P x e |
y |
|
Q e |
y |
|
|
|
||||||||||
б) Полагая |
|
, |
|
|
|
|
1 , подставляем их в |
|||||||||||
|
|
|
y |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
выражение (2) и убеждаемся, что это уравнение в полных дифференциалах.
|
x |
|
|
|
x |
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||
|
|
y |
|
|
|
|
|
||||||
x e |
|
|
|
e |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
|
|
|
|
|
|
y |
|
|
x |
e |
|
|
|
|
|
|
|
|
y |
. |
|||||||
y |
|
|
|
|
x |
|
y2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
Для нахождения функции и интегрируем ее частные дифференциалы по формулам (4), считая в первом случае у постоянной величиной, а во втором – х
24

|
|
|
|
|
|
|
|
x |
|
x |
2 |
|
|
|
x |
y , |
|
|
|
|
|
|
|
|
|
|
|||||||
Pdx |
x e y dx |
|
ye y |
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
x |
x . |
|||
Qdy |
e |
y |
|
|
ye |
y |
|
|||||||||
|
|
y |
|
|
|
|
|
|||||||||
|
|
|
|
|
1 dy |
|
|
|||||||||
Подставляя из первого выражения все члены, зависящие от x, во второе и приравнивая постоянной интегрирования,
|
x2 |
|
x |
|
|
получим |
ye |
y |
C . |
|
|
|
|
||||
2 |
|
|
уравнения: а) x2 |
y dx xdy 0; |
|
5.2. Решить |
|||||
б) xy2 y dx xdy 0 при условии |
y(1) =1. |
||||
Решение. а) Здесь P x2 y ; Q = - x. Подставляя Р и Q в
выражение (6), |
получим |
|
|
|
|
|
|
|
|
|
|
|
|
||
d |
|
2dx |
; |
ln |
|
|
|
2ln |
|
x |
|
; |
|
1 |
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Умножим на интегрирующий множитель левую часть
|
|
y |
|
1 |
|
|
уравнения 1 |
|
|
|
dx |
|
dy 0 . |
x |
2 |
x |
||||
|
|
|
|
|
||
Проверим по условию (5) - является ли это уравнение в полных дифференциалах
|
|
|
y |
|
|
|
1 |
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
. |
|||
y |
|
|
|
|
x |
|
x2 |
||||||
|
|
|
|
|
|
|
|
||||||
Находим неопределенные интегралы
|
Pdx |
|
|
|
y |
|
y |
y ; |
|
|
x |
2 |
|
x |
|||||
|
|
1 |
|
dx x |
|
||||
Qdy 1x dy xy x .
25
Так как во втором выражении нет членов, зависящих только от у, то есть y 0 , то общее решение получается
из первого результата |
x |
|
y |
C . |
|
|
|
|
|||||||||
|
x |
|
|
|
|
||||||||||||
б) Здесь P xy2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y, |
Q x . |
Подставляя |
|||||||||||||||
выражение (7), получим |
|
|
|
|
|
|
|
|
|
|
|
||||||
d |
1 |
|
|
|
|
|
1 2xy 1 dy |
2dy |
|||||||||
xy2 |
y |
|
y |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ln |
|
|
|
2ln |
|
y |
|
, |
|
1 |
. |
|
||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Р и Q в
,
Умножим |
на |
|
|
интегрирующий |
множитель левую часть |
|||||||||||||
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
уравнения x |
|
dx |
|
|
dy 0 . |
|
|
|
|
|
||||||||
y |
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||
Проверим, является ли это уравнение в полных |
||||||||||||||||||
дифференциалах по условию (5) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
y |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
y |
|
|
|
|
x |
|
y2 |
|||||
Поскольку равенство выполнено, то частный интеграл находим по формуле (3), считая, что x0 1, y0 1, C 0 .
x |
|
|
|
|
|
2 |
|
|
|
|
x |
|
|
y |
|
2 |
|
|
|
|
|||
1 |
y |
1 |
|
x |
|
|
1 |
|
|
x |
|
x |
|
|
|||||||||
1 |
x |
dx 1 |
dy |
x |
|
|
|
|
|
|
|
|
|
3 |
0, |
||||||||
|
2 |
|
|
y |
y |
|
|
|
|||||||||||||||
|
|
y |
|
y |
2 |
|
|
|
1 |
1 |
|
2 |
|
y 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x2 y 2x 3y. |
|
|
|
|
|
|
|
|
|||||||||
|
1.6. Уравнение Лагранжа и Клеро |
|
|
|
|
|
|
||||||||||||||||
|
1°. Дифференциальное уравнение вида |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
y x y y |
|
|
|
|
|
|
|
|
|
(1) |
||||||||
называется уравнением Лагранжа.
26

Если положить y p и принять x за функцию, то после
дифференцирования уравнение (1) сводится к линейному относительно x
p p dx |
p x p 0 , |
(2) |
|
|
dp |
|
|
где p - независимая переменная.
Интегрируя уравнение (2) и подставляя найденное значение x в уравнение (1), получим общее решение уравнения Лагранжа в параметрическом виде. Общее решение
в обычном виде |
можно получить исключением параметра |
p . |
||
Кроме того, |
из |
условия p p 0 , |
уравнение (1) может |
|
иметь особые и частные решения вида |
|
|
||
|
|
y x p p . |
(3) |
|
2°. Если |
в |
уравнении Лагранжа y y то получим |
||
уравнение Клеро |
|
|
||
|
|
y xy y . |
(4) |
|
Полагая |
у' = р и дифференцируя, |
находим, что р = С |
и |
|
x p . |
|
|
|
|
Отсюда общее решение уравнения (4) имеет вид |
|
|||
|
|
y Cx C , |
(5) |
|
а особое решение получается исключением параметра p из уравнений
y px p ; x p . |
(6) |
Общее решение представляет собой семейство прямых, а особое является огибающей этого семейства.
6.1. Решить уравнения: a) y 2xy |
1 y 2 ; б) y xy |
1 |
. |
y2 |
Решение. а) Данное уравнение есть уравнение Лагранжа. Полагаем у' = р, тогда уравнение примет вид
y 2xp |
1 p2 . |
Продифференцируем его
27
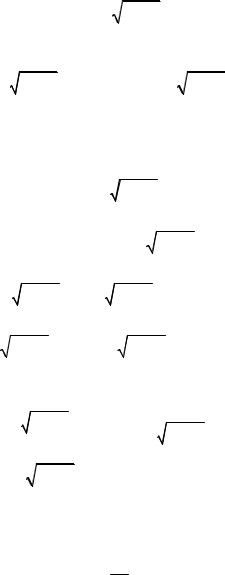
dy 2 pdx 2xdp |
|
pdp |
. |
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
1 p2 |
|
|
|||
Так как dy pdx , то |
|
|
|
|
|
|
|
|
|
|
pdx 2xdp |
pdp |
или |
dx |
|
2 |
x |
1 |
. |
||
1 p2 |
dp |
|
|
|||||||
|
|
|
p |
1 p2 |
||||||
Таким образом, решение свелось к линейному уравнению. Используя замену x = uv; x u v v u , где u, v - функции от p, будем иметь
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
. |
|
|
|
||||||||||||
|
|
|
|
u v u v |
|
p |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 p2 |
|
|
|
|
|||||||||||
|
dv |
2 |
dp |
|
v |
|
1 |
|
|
|
|
|
|
|
|
du |
|
|
|
|
p2 |
|||||||||||||
Отсюда |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
; |
|
|||||||||
v |
|
p |
|
p2 |
|
|
|
|
dp |
1 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
||||||||||||||||
|
|
|
u |
|
|
p2 1 |
|
dp |
|
|
|
dp |
|
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
1 p |
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интегрируя первый интеграл по частям, получим |
||||||||||||||||||||||||||||||||||
|
u |
1 p 1 p2 |
|
1 ln |
|
p 1 p2 |
|
C . |
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Окончательно общий интеграл в параметрической форме |
||||||||||||||||||||||||||||||||||
примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
1 p |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
|
|
|
|
|
|
|
ln |
p 1 p2 |
; |
|||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||
|
|
|
|
p |
|
|
|
|
2 p |
|
|
|
|
|
|
2 p |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 px 1 p2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Это уравнение Клеро. Полагаем у' = р, тогда уравнение |
||||||||||||||||||||||||||||||||||
примет вид y px |
1 |
|
. Дифференцируем его |
|||||||||||||||||||||||||||||||
p2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dy pdx xdp p23 dp .
Так как dy = pdx, то
28

|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
xdp |
dp 0 |
или dp x |
0 . |
|
|
|
|
|
|||||||||||||||||||
|
3 |
3 |
|
|
|
|
|
|||||||||||||||||||||
|
|
p |
|
|
2 |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
||||||||
Отсюда, либо dp=0, либо x |
|
. Если положить, что |
dp = 0, |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
то p = С и |
y Cx |
1 |
|
- будет общим решением данного |
||||||||||||||||||||||||
C2 |
||||||||||||||||||||||||||||
уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
3 |
|
|
||||
Если положить, что |
x |
|
, |
то |
y |
|
|
|
, |
и |
||||||||||||||||||
p3 |
|
p2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
p2 |
|
||||||||
получим особое решение |
x |
2 |
|
|
, y |
3 |
. Исключая отсюда |
|||||||||||||||||||||
|
p3 |
|
|
|||||||||||||||||||||||||
|
p, находим |
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
||||||||||
параметр |
особое |
решение |
в |
явном |
виде |
|||||||||||||||||||||||
y 32 3 2x2 .
Докажем, что семейство прямых, определяемых общим решением, представляет собой семейство касательных к особой интегральной кривой, т.е. особое решение является огибающей этого семейства.
Уравнение касательной к особой кривой в некоторой точке
x0 , y0 имеет вид |
y y0 |
y0 x x0 , |
где производная y0 , |
||||||||
найденная из уравнения кривой в точке x0 , равна y0 3 |
2 |
. |
|||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x0 |
|
Подставляя сюда значение y |
0 |
3 3 |
2x2 |
и упрощая, находим |
|||||||
|
|
|
2 |
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
y x 3 |
2 |
|
1 3 2x02 . |
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
x0 |
2 |
|
|
|
|||
Если считать, |
что |
C 3 |
2 |
, то |
уравнение семейства |
||||||
x |
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
||
касательных к особой интегральной кривой в произвольной
29
точке x , y |
|
примет вид |
y Cx |
1 |
, т.е. особое решение |
|
C2 |
||||
0 |
0 |
|
|
|
является огибающей этого семейства.
1.7. Уравнения 1-го порядка, не разрешенные относительно производной
1 . Если дифференциальное уравнение является уравнением высшей степени относительно производной
. Если дифференциальное уравнение является уравнением высшей степени относительно производной
f x, y, y 0 , |
(1) |
то, разрешая его относительно y , например, для случая второй степени, получим два уравнения
y f1 x, y |
и y f2 x, y . |
(2) |
Геометрически это означает, что через каждую точку М некоторой плоской области проходят две интегральные кривые. Общее решение уравнения (1) в этом случае примет вид
F1 x, y,C 0; |
F2 x, y,C 0 . |
(3) |
Кроме того, уравнение (1) может иметь особое решение, которое может быть получено в результате исключения у' = р из системы уравнений
f x, y, p 0; f p x, y, p 0 . |
(4) |
Геометрически особый интеграл представляет огибающую |
|
семейства кривых (3) |
|
F x, y,C F1 x, y,C F2 x, y,C 0 |
(5) |
и может быть получен еще исключением С |
из системы |
уравнений |
|
F x, y,C 0; FC x, y,C 0 . |
(6) |
Следует заметить, что кривые (4), (6), не всегда являются решениями уравнения (1) и в каждом конкретном случае необходима проверка.
2°. Если уравнение имеет вид
30
