Учебное пособие 1305

Рис. 9

Найдём площадь криволинейного сектора, ограниченного линией ρ = f (ϕ) и двумя лучами: ϕ =α и ϕ = β , выходящи-

ми из полюса. Воспользуемся методом дифференциалов. Выделим произвольный внутренний угол ψ (α, β). Рас-

смотрим площадь S(ψ) части указанного криволинейного сектора, заключенную между углами α и ψ . Назначим углу ψ приращение ∆ψ = dψ .

ρ=f(ϕ)

B C

Aα

β dψ

ментарного криволинейного сектора» OBA (рис.10). Однако, дифференциал dS как главная часть приращения равен пло-

щади кругового сектора OCA , т.е. dS = 12 ρ2dψ . 60

Интегрируя равенство dS = 12 ρ2dψ в пределах от ψ =α

до ψ = β , получим искомую формулу для площади криволинейного сектора:

Пример 3.3.1. Вычислить площадь фигуры, ограниченной линией ρ = acos 2ϕ .

Решение: Найдем пределы интегрирования из условия

Рис. 11

Поскольку фигура содержит четыре симметричных элемента, то вычислим площадь четвертой части фигуры:

61

S = a2 .

3.4. Вычисление длины дуги

1. Пусть в прямоугольных координатах задана гладкая (не содержащая угловых точек) кривая AB , являющаяся графиком

функции y = f (x), имеющей на отрезке [a,b] непрерывную

производную.

Под длиной дуги AB подразумевается предел длины вписанной в эту дугу ломаной линии, число звеньев которой стремится к бесконечности, а длина наибольшего звена стремится к нулю.

Используем метод интегральных сумм для нахождения формулы длины дуги. Разобьем отрезок [a,b] на n частей точ-

ками xi (i = 0,1,..., n). Пусть на кривой этим точкам соответс т- вуют точки M i (xi , f (xi )). Рассмотрим i −тый участок разбиения (рис. 12).

y = f (x) M i

∆Li ∆yi

M i−1

∆xi = xi − xi−1

Рис. 12

Длина хорды M i−1M i может быть найдена по теореме

Пифагора для прямоугольного треугольника с длинами катетов

∆yi и ∆xi :

62

дуги находится с помощью замены переменной в интеграле

формально можно принять параметром полярный угол ϕ , тогда кривую оказывается возможным задать параметрически

x = ρ(ϕ)cosϕ,y = ρ(ϕ)sinϕ.

Вычисляя производные x (ϕ)= ρ (ϕ)cosϕ − ρ(ϕ)sinϕ ,

′ ′

y′(ϕ)= ρ′(ϕ)sinϕ + ρ(ϕ)cosϕ , имеем

(x′()t )2 +(y′()t )2 = (ρ′(ϕ)cosϕ −ρ(ϕ)sinϕ)2 +(ρ′(ϕ)sinϕ + ρ(ϕ)cosϕ)2 =

64

= (ρ′(ϕ))2 + (ρ(ϕ))2 .

Используя полученный результат, находим формулу для вычисления длины дуги, заданной в полярных координатах:

β

L = ∫(ρ(ϕ))2 + (ρ′(ϕ))2 dϕ.

α

Пример 3.4.2. Вычислить длину кардиоиды ρ =1+sinϕ. Решение: Кардиоида имеет вид, представленный на рис. 13.

ρ =1+sinϕ

ρ

O

Рис. 13 Кардиоида имеет две симметричные части. Вычислим

длину правой половины кривой:

3.5. Вычисление объема тела

Пусть требуется найти объем тела, ограниченного замкнутой поверхностью, которое проектируется на отрезок [a,b] оси Ox , причем известна зависимость площади поперечного сечения тела S = S(x) плоскостью, перпендикулярной оси Ox . Предполагается, что S = S(x) является непрерывной функцией x на отрезке [a,b].

Используем метод дифференциала. Через произвольную точку x проведем плоскость σ , перпендикулярную оси Ox . Площадь поперечного сечения равна S(x). Через точку x + dx

проведём другую плоскость, параллельную первой. Тогда из объёма тела будет выделен «элементарный слой» dV , соответствующий приращению объема. Объем «элементарного слоя» приближенно может быть посчитан как объем цилиндра с ос-

нованием S(x) и высотой dx : dV = S(x)dx .

Искомую величину объема находим интегрированием dV в пределах от a до b

V = ∫b S(x)dx .

a

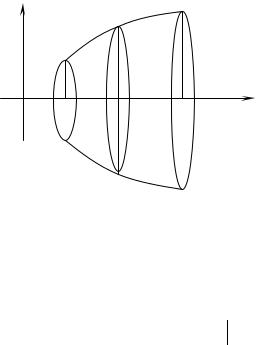
Вычисление объема тела вращения (рис.14), образованного вращением вокруг оси Ox криволинейной трапеции, представляет собой частный случай предыдущей задачи. Пусть криволинейная трапеция, ограниченная сверху непрерывной

кривой y = f (x), прямыми линиями x = a , x = b и ось Ox .

Любое сечение данного тела плоскостью, перпендикулярной оси Ox , есть круг радиуса R = y = f (x) . Поэтомуплощадь по-

перечного сечения равна

S(x) =πy2 =π[f (x)]2 и dV =π[f (x)]2 dx .

Объем тела вращения вокруг оси Ox равен

66

Рис. 14

Пример. 3.5.1. Найти объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями y = x3 , x =1, y = 0 .

Решение:

y = f (x) ≥ 0 , заданной на отрезке [a,b] и непрерывной вместе

с ее производной y′(x). Найдём площадь поверхности враще-

ния, образованной вращением кривой AB вокруг оси Ox . Для вывода формулы площади поверхности вращения ис-

пользуем метод дифференциала. Через произвольную внутреннюю точку x [a,b] проведем перпендикулярную оси Ox плоскость σ .

67

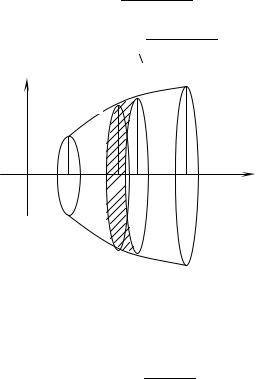
Плоскость σ пересекает поверхность по окружности радиуса y = f (x). Величина S части поверхности вращения,

расположенная левее плоскости σ , является функцией x . Пусть через точку x + dx проведена другая плоскость, параллельная плоскости σ . Тогда две параллельные плоскости выделят бесконечно узкую полосу поверхности (рис. 15.), площадь которой dS можно вычислить по формуле площади боковой поверхности усечённого конуса, образующая которой равна dl , а радиусы оснований равны y и y + dy :

dS =π(y + (y + dy))dl = 2πydl +πdydl .

Пренебрегая слагаемым πdydl как величиной более высокого порядка малости по сравнению с dl , получаем

dS = 2πydl . Поскольку dl = 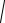1+ (y′(x))2 dx , то

b

S = 2π∫y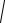1+ (y′(x))2 dx.

a

y

y=f(x)

Рис. 15

Пример. 3.6.1. Найти площадь поверхности шара радиу-

са a .

Решение:

Будем считать, что поверхность получена в результате вращения полуокружности y = a2 − x2 вокруг оси Ox .

68

Если поверхность вращения вокруг оси Ox образована кривой, заданной параметрическими уравнениями x = x(t), y = y(t),

t1 ≤ t ≤ t2 , то площадь поверхности вращения равна

t2

S = 2π ∫y(t) (x′(t))2 + (y′(t))2 dt.

t1

Пример 3.6.2. Найти площадь поверхности, образованной вращением циклоиды вокруг оси Ox .

Решение:

Первая арка циклоиды описывается уравнениями

x = t −sin t,y =1−cost,

где 0 ≤ t ≤ 2π . Тогда площадь поверхности вращения равна